循环系统优化算法，原理详解，MATLAB代码免费获取

原创已于 2025-01-07 15:42:29 修改 · 945 阅读

CC 4.0 BY-SA版权

文章标签：

于 2024-07-18 09:15:14 首次发布

循环系统优化算法（Circulatory System Based Optimization，CSBO）是基于人体血管的功能建模的元启发式优化算法，具有两个不同的回路，即肺回路和全身回路。在该算法中，肺循环处理的是缺氧血，相当于较弱的种群，体循环处理的是含氧血，相当于目标值较好的种群。所提出的CSBO算法在现实世界的各种复杂函数上进行了测试，并用标准的元启发式算法进行了验证。结果表明，CSBO算法成功地获得了最优解，避免了局部最优。

该成果于2022年发表在工程技术领域一区SCI期刊“Engineering Applications of Computational Fluid Mechanics”上，目前被引35次。

1、算法原理

（1）引言

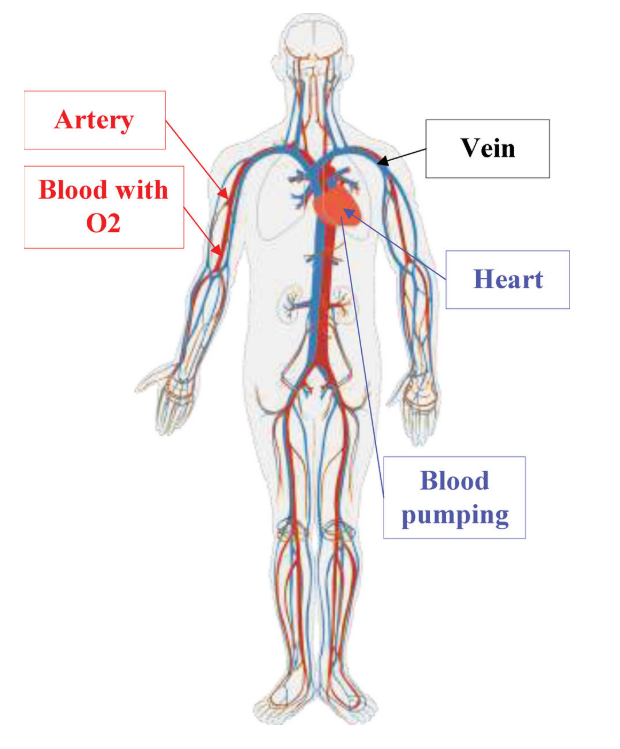
根据图中身体常规表现的循环系统的简单吸气模型，身体的血管在功能上分为两个不同的回路：肺回路和全身回路。右心室是肺回路的泵，使血液在肺部循环。左心室是全身回路的泵，为身体的组织细胞提供血液供应。肺循环将缺氧血液从右心室输送到肺部，在那里血液获得新的血液供应。然后它将富氧血液返回左心房。血液在大多数情况下被认为是牛顿流体。循环系统的主要变量是流量、压力和容量。循环系统的压力-流量建模可以从两个角度进行检查，即搏动和非搏动，这在受搏动角度启发的模型中被考虑。

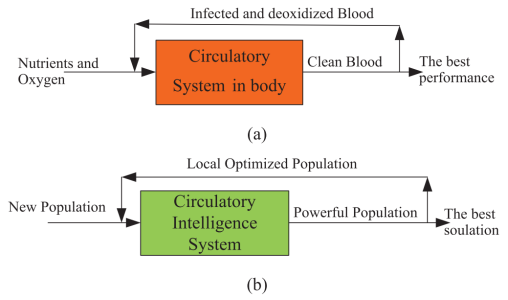
在CSBO算法中，与其他元启发式优化算法一样，首先，基于问题范围内的随机函数生成初始种群，这里的随机函数代表血滴的质量。血滴的位置代表了搜索空间中优化问题的可能解决方案，循环系统充当这个群体的算子，以细化和加强它们，并界定较弱的群体。换句话说，在搜索空间（身体）中的解决方案（血液）质量在基于身体中血液循环系统的功能的迭代过程中得到改善。下图显示了如何将循环系统中血液的演变过程等效地建模为优化器系统。

（2）初始化

首先，CSBO算法与任何其他元启发式算法一样，以初始总体或血液质量BMi = (BMi,1,BMi,2，…，Bmi,D)，对于具有维数D (D = 1:D)的典型问题，其最小BMmin = (BMmin,1，…，BMmax,D)和maximum BMmax = (BMmax,1，…，Bmmax,D)值的问题参数范围如下:

如前所述，这个初始群体在体内扮演着与血液颗粒或团块相同的角色。

（3）血管中血块的运动

静脉中的第i个血液质量，BMi，基于施加的力或压力而移动。质量总是在具有更优条件的方向上移动。因此，它的目标函数（力或压力的大小）的值减小了。CSBO可以将心脏中的动脉阻塞建模为陷入局部最优解。CSBO不希望这种情况发生在真实的世界中。随着身体的继续工作，算法将很好地继续其优化过程。循环周期的这一步是基于粒子位置及其目标函数值建模的，如下所示：

事实上，Kij决定了动脉中第i个血团（BMi）的运动方向。pi是一个介于0和1之间的值，取决于问题的维度。它决定了位移量，并在每个循环周期中向更好的值移动。

（4）肺循环中的人群或血液质量流量

如前所述，肺循环处理脱氧血液，相当于优化中的较弱群体。事实上，在CSBO中，在每次迭代时，对群体进行排序，并且NR数量的最弱群体进入肺循环并被引导到肺部以获得氧气

在公式中，randn表示随机正态数，它表示当前算法迭代，randc表示来自柯西概率分布的随机向量，D是优化问题维数的倍数。肺循环也改变了该人群的pi，如下所示：

（5）体循环中的人口或血液质量流量

如上所述，最弱分类群体的NR数量进入肺循环。具有更好拟合值的其余群体（NL = Npop-NR）以新的量进入体循环，以便在体内循环，如下所示：

系统循环也校正了这组人口的圆周率，如下所示：

其中FWorst和FBest是直到当前迭代为止获得的成本函数的最差和最佳值。

优化周期将持续指定的迭代次数。类似于其他元启发式算法，每个成员的人口将接受新的位置，如果它得到一个更好的值的适应度函数。

算法1中总结了CSBO算法伪代码。

2、结果展示

3、MATLAB核心代码

% 循环系统优化算法（Circulatory System Based Optimization，CSBO）
function [avg_fitness_curve, Best_pos, Best_score, curve, search_history, fitness_history] = ECO(N, Max_iter, lb, ub, dim, fobj)
H = 0.5;  % Learning habit boundary
G1 = 0.2; % proportion of primary school (Stage 1)
G2 = 0.1; % proportion of middle school (Stage 2)
% BestF: Best value in a certain iteration
% WorstF: Worst value in a certain iteration
% GBestF: Global best fitness value
% AveF: Average value in each iteration
G1Number = round(N * G1); % Number of G1
G2Number = round(N * G2); % Number of G2
if (max(size(ub)) == 1)
    ub = ub .* ones(1, dim);
    lb = lb .* ones(1, dim);
end
%% Initialization
X0 = initializationLogistic(N, dim, ub, lb); %Logistic Chaos Mapping Initialization
X = X0;
% Compute initial fitness values
fitness = zeros(1, N);
for i = 1:N
    fitness(i) = fobj(X(i, :));
end
[fitness, index] = sort(fitness); % sort
GBestF = fitness(1); % Global best fitness value
AveF = mean(fitness);
for i = 1:N
    X(i, :) = X0(index(i), :);
end
curve = zeros(1, Max_iter);
avg_fitness_curve = zeros(1, Max_iter);
GBestX = X(1, :); % Global best position
GWorstX = X(end, :); % Global worst position
X_new = X;
search_history = zeros(N, Max_iter, dim);
fitness_history = zeros(N, Max_iter);
%% Start search
for i = 1:Max_iter
    if mod(i,100) == 0
      display(['At iteration ', num2str(i), ' the fitness is ', num2str(curve(i-1))]);
    end
    avg_fitness_curve(i) = AveF;
    R1 = rand(1);
    R2 = rand(1);
    P = 4 * randn * (1 - i / Max_iter);
    E = (pi * i) / (P * Max_iter);
    w = 0.1 * log(2 - (i / Max_iter));
    for j = 1:N
        % Stage 1:Primary school competition
        if mod(i, 3) == 1
            if j >= 1 && j <= G1Number %Primary school Site Selection Strategies
                X_new(j, :) = X(j, :) + w * (mean(X(j, :)) - X(j, :)) .* Levy(dim); 
            else %Competitive Strategies for Students (Stage 1)
                X_new(j, :) = X(j, :) + w * (close(X(j, :),1,X) - X(j, :)) .* randn(1);
            end
        % Stage 2:Middle school competition
        elseif mod(i, 3) == 2
            if j >= 1 && j <= G2Number %Middle school Site Selection Strategies
                X_new(j, :) = X(j, :) + (GBestX - mean(X)) * exp(i / Max_iter - 1) .* Levy(dim);
            else %Competitive Strategies for Students (Stage 2)
                if (R1 < H)
                    X_new(j, :) = X(j, :) - w * close(X(j, :),2,X) - P * (E * w *close(X(j, :),2,X) - X(j, :));
                else
                    X_new(j, :) = X(j, :) - w * close(X(j, :),2,X) - P * (w * close(X(j, :),2,X) - X(j, :));
                end
            end
        % Stage 3:High school competition
        else
            if j >= 1 && j <= G2Number %High school Site Selection Strategies
                X_new(j, :) = X(j, :) + (GBestX - X(j, :)) *randn - (GBestX - X(j, :)) * randn;
            else %Competitive Strategies for Students (Stage 3)
                if (R2 < H)
                    X_new(j, :) = GBestX - P * (E * GBestX - X(j, :));
                else
                    X_new(j, :) = GBestX - P * (GBestX - X(j, :));
                end
            end
        end
        % Boundary control
        Flag4ub=X_new(j,:)>ub;
        Flag4lb=X_new(j,:)<lb;
        X_new(j,:)=(X_new(j,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        % Finding the best location so far
        fitness_new(j) = fobj(X_new(j, :));
        if fitness_new(j) >  fitness(j)
            fitness_new(j) = fitness(j);
            X_new(j, :) = X(j,:);
        end
        if fitness_new(j) < GBestF
            GBestF = fitness_new(j);
            GBestX = X_new(j, :);
        end
    end
    X = X_new;
    fitness = fitness_new;  
    curve(i) = GBestF;
    Best_pos = GBestX;
    Best_score = curve(end);
    search_history(:, i, :) = X;
    fitness_history(:, i) = fitness;
    % Sorting and updatin
    [fitness, index] = sort(fitness); % sort
    for j = 1:N
        X0(j, :) = X(index(j), :);
    end 
    X = X0;
end
%%  Levy search strategy
function o = Levy(d)
    beta = 1.5;
    sigma = (gamma(1 + beta) *sin(pi * beta / 2) / (gamma((1 + beta) / 2) * beta * 2^((beta - 1) / 2)))^(1 / beta);
    u = randn(1, d) * sigma;
    v = randn(1, d);
    step = u ./ abs(v).^(1 / beta);
    o = step;
end    
%%  Choosing the Nearest School
function o = close(t,G,X)
  m = X(1,:);
  if G == 1
     for s = 1:G1Number
        school = X(s, :);
        if  sum(abs(m - t)) > sum(abs(school - t))
            m = school;
        end
     end
  else
     for s = 1:G2Number
        school = X(s, :);
        if  sum(abs(m - t)) > sum(abs(school - t))
            m = school;
        end
     end
  end
  o = m;  
end
%% Logistic chaotic mapping initialization
function Positions=initializationLogistic(pop,dim,ub,lb)
    Boundary_no= length(ub); % number of boundaries
    for i = 1:pop
        for j = 1:dim
            x0 = rand;
            a = 4;
            x = a*x0*(1-x0);
            if Boundary_no == 1
                Positions(i,j) = (ub-lb)*x + lb;
                if Positions(i,j)>ub
                    Positions(i,j) = ub;
                end
                if Positions(i,j)<lb
                    Positions(i,j) = lb;
                end
            else
                Positions(i,j) = (ub(j)-lb(j))*x + lb(j);
                if Positions(i,j)>ub(j)
                    Positions(i,j) = ub(j);
                end
                if Positions(i,j)<lb(j)
                    Positions(i,j) = lb(j);
                end
            end
            x0 = x;
        end
    end
end

参考文献

[1]Ghasemi M, Akbari M A, Jun C, et al. Circulatory System Based Optimization (CSBO): an expert multilevel biologically inspired meta-heuristic algorithm[J]. Engineering Applications of Computational Fluid Mechanics, 2022, 16(1): 1483-1525.

完整代码获取

后台回复关键词：

TGDM811

点击下方卡片关注，获取更多代码