2024年智能算法优化PID参数，ITAE、ISE、ITSE、IAE四种适应度函数随意切换，附MATLAB代码...

PID 参数整定就是确定比例系数（Kp ）、积分系数（Ki）和微分系数（Kd ）的过程，以便使 PID 控制器能够在系统中实现稳定、快速、准确的响应。

本期的主题

采用四种2024年的智能优化算法优化PID的三个参数，以便达到较好的响应曲线。

四种算法分别是：牛顿-拉夫逊优化算法，美洲狮优化算法，足球队训练算法，冠豪猪优化算法。四种算法都是2024年最新的优化算法。

具体原理

首先，采用simulink搭建具体的模型，模型简单易修改！

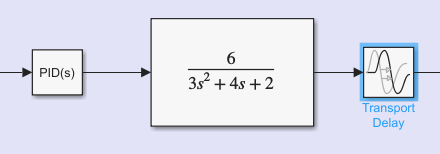
只需要打开simulink模型，修改这里的函数即可。后面的延迟环节也可以在其中随意修改！

然后，在主函数里边不断地调用该模型，并以PID参数寻优常用的四种评价(ITAE/ISE/ITSE/IAE)为适应度函数指标进行寻优。

四种适应度函数公式如下：

平方误差积分(ISE):

绝对误差积分(IAE):

时间乘方误差积分(ITSE):

时间乘绝对误差积分(ITAE):

代码中已经集成好，方便修改适应度函数：

xz = 1;  %可选四种适应度函数：平方误差积分 /时间乘以绝对误差积分  /时间乘方误差积分 /绝对误差积分
if xz == 1
    fobj = @(x)ISE_object(x);   %平方误差积分
elseif xz == 2
    fobj = @(x)ITAE_object(x);  %时间乘以绝对误差积分
elseif xz == 3
    fobj = @(x)ITSE_object(x);  %时间乘方误差积分
elseif xz == 4
    fobj = @(x)IAE_object(x);   %绝对误差积分
end

最后，以ITAE指标为例进行展示。将寻优得到的三个最佳参数回代适应度函数，得到不同算法的响应曲线对比图。如下所示。

响应曲线对比图：

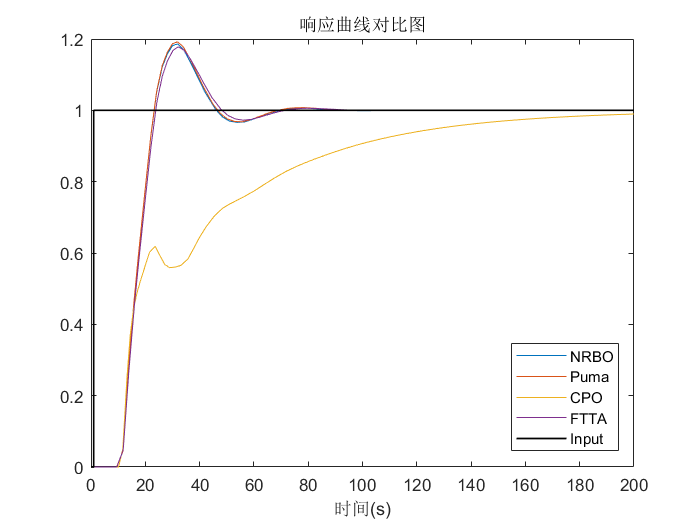
可以看到CPO算法的寻优效果最差，其他三种的寻优效果相当。

误差曲线图：

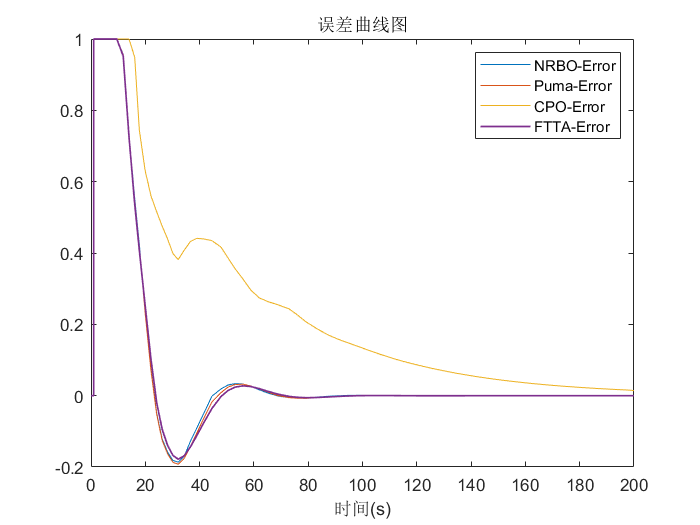
四种算法的寻优过程收敛曲线图：

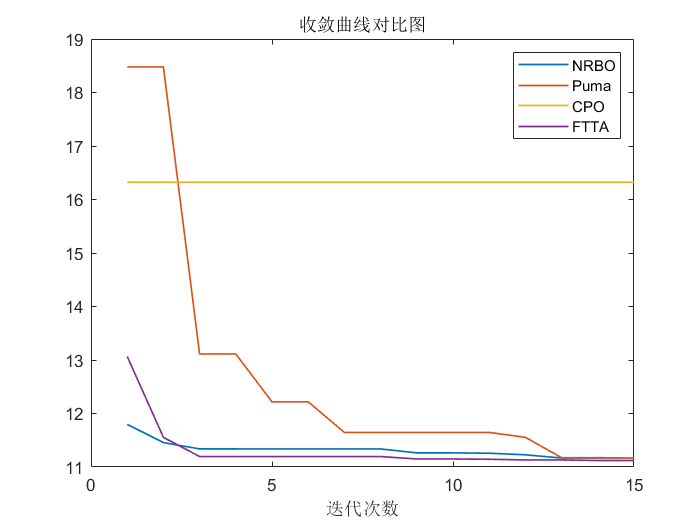
最后，四种算法寻优得到最佳PID参数如下：

	NRBO	Puma	CPO	FTTA
Kp	0.08741	0.075192	0.12841	0.07292
Ti	3.5447	3	15.2719	3
Td	0.10708	5.438	0.16982	3.9195

代码目录如下：

考虑到大家的matlab版本可能不同，作者在这里保存了不同版本的simulink模型。

大家选取相应的版本模型，并在主函数和四个适应度函数文件里边，把TFmodel22改成TFmodelXX对应的版本即可运行！

另外再推荐几篇往期写的PID参数整定文章：

三种智能算法优化PID参数软件，MATLABAPP开发

改进的粒子群算法整定PID参数，并与灰狼算法进行比较，附MATLAB代码

灰狼算法整定PID参数，传递函数可以任意修改，附MATLAB代码