偏度和峰度是高阶统计量,它提供了统计分布的内在属性。
-
偏度是衡量分布中不对称程度的三阶统计量。
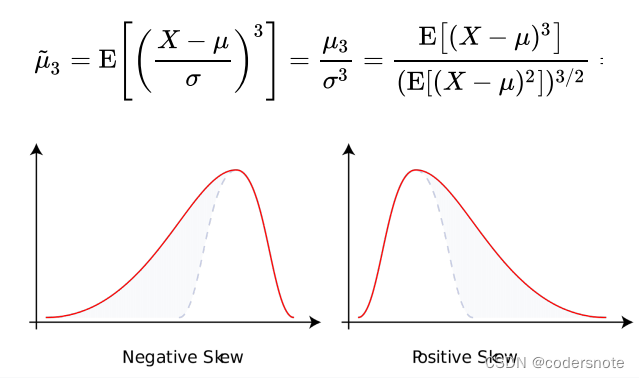
-
峰度是一种四阶统计量,它给出了一种统计分布尖峰程度的度量。
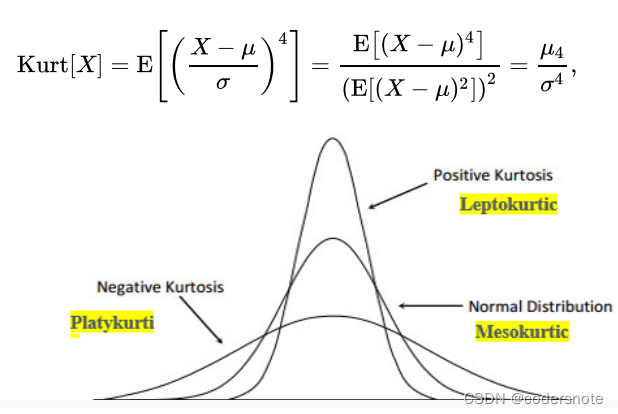
-
甚至可以使用进一步的高阶统计(例如,6th-order hex a kurtosis),尽管它们在实践中提供收益递减。
 本文是Ollydbg的使用教程,包括基础操作如修改程序标题,使用API断点获取编辑框输入,以及解密技巧。在实例中,介绍了如何通过API断点法获取GetDlgItemTextA函数,以及如何利用EIP、EAX等寄存器进行程序分析,提出了两种解密方法:跳过或 nop 掉陷阱跳转。
本文是Ollydbg的使用教程,包括基础操作如修改程序标题,使用API断点获取编辑框输入,以及解密技巧。在实例中,介绍了如何通过API断点法获取GetDlgItemTextA函数,以及如何利用EIP、EAX等寄存器进行程序分析,提出了两种解密方法:跳过或 nop 掉陷阱跳转。
偏度和峰度是高阶统计量,它提供了统计分布的内在属性。
偏度是衡量分布中不对称程度的三阶统计量。

峰度是一种四阶统计量,它给出了一种统计分布尖峰程度的度量。

甚至可以使用进一步的高阶统计(例如,6th-order hex a kurtosis),尽管它们在实践中提供收益递减。

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


