统计学习方法——统计学习基础（一）

统计学习概论（一）

统计学习

统计学习的特点

• 建立在计算机与网络的基础上
• 以数据为研究对象
  • 基本假设：同类数据具有一定的统计规律性。
• 以方法为中心
  • 常用方法
    • 监督学习
    • 非监督学习
    • 半监督学习
    • 强化学习
• 目标是对数据进行预测与分析

统计学习的方法

• 监督学习
  • 从给定的、有限的、用于学习的训练集出发
  • 假设数据独立同分布
  • 假设要学习的模型属于某个函数的集合，称为假设空间
  • 采用评价标准从假设空间选择最优的模型

可以总结出统计学习的三要素：模型、策略和算法。

监督学习

监督学习的任务是学习一个模型，使模型能够对任意给定的输入能做出一个好的预测。

基本概念

• 输入空间：所有与样本相关的可以获得的信息，记作$X$
• 特征空间：所有特征向量存在的空间，一般与输入空间不加区分
• 输出空间：一般为分类（预测）的结果，记作$Y$
• 联合概率分布
  • 监督学习假设输入和输出的随机变量$X$和$Y$遵循联合概率分布$P(X,Y)$。
  • 训练集和测试集的数据被看作依联合概率分布$P(X,Y)$独立同分布产生的。
• 假设空间：模型属于由输入空间到输出空间的映射的集合，这个集合就是假设空间，记为$\mathcal{F}$。
  F = { f ∣ Y = f ( X ) } \mathcal{F}=\left\{f|Y=f(X)\right\} F={f∣Y=f(X)}
  此时$\mathcal{A}$通常是由一个参数向量决定的函数族：
  F = { f ∣ Y = f θ ( X ) , θ ∈ R n } \mathcal{F}=\left\{f|Y=f_\theta(X),\theta\in R^n\right\} F={f∣Y=fθ​(X),θ∈Rn}
  参数向量$\theta$取值于$n$维欧氏空间$R^n$，称为参数空间。
• 监督学习的模型：可以是概率模型或非概率模型，由条件概率分布$P(Y|X)$或决策函数$Y=f(x)$表示。

问题形式化

通过一个简单的图展示监督学习的过程：

• 训练集： T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T=\left\{(x_1,y_1),...,(x_N,y_N)\right\} T={(x1​,y1​),...,(xN​,yN​)}，其中每一个都称为样本点，$x_i$为输入值，$y_i$为输出值。
• 训练的模型：表示为$\hat{P}(Y|X)$或$Y=\hat{f}(X)$
• 预测的结果：假设待预测的样本为$x_{N+1}$，则结果记为$y_{N+1}=arg\underset{y_{N+1}}{\max }\hat{P}(y_{N+1}|x_{N+1})$或$y_{N+1}=\hat{f}(x_{N+1})$

统计学习的三要素

方法=模型+策略+算法

模型

• 模型的假设空间包含所有可能的条件概率分布或决策函数 。

策略

• 用于考虑如何选择最优的模型
• 相关函数
  • 损失函数
    • 0-1损失函数：
      $$L\left(Y,f\left(X\right)\right)=\{\begin{array}{l}1Y̸=f\left(X\right)\\ 0Y=f\left(X\right)\end{array}$$
    • 平方损失函数：
      $$L\left(Y,f\left(X\right)\right)={\left(Y-f\left(X\right)\right)}^2$$
    • 绝对损失函数：
      $$L\left(Y,f\left(X\right)\right)=\left|Y-f\left(X\right)\right|$$
    • 对数损失函数：
      $$L\left(Y,P\left(Y|X\right)\right)=-\log P\left(Y|X\right)$$
  • 风险函数：
    • 风险函数（期望损失）
      损失函数的期望（由于输入输出遵循联合分布$P\left(X,Y\right)$）称为风险函数或期望损失:
      $$R_{\exp }\left(f\right)=E_p\left[L\left(Y,f\left(X\right)\right)\right]={\int }_{\mathcal{X}\times \mathcal{Y}}L\left(y,f\left(x\right)\right)P\left(x,y\right)dxdy$$
    • 经验风险（经验损失）
      对于训练集的平均损失称为经验风险或经验损失：
      $$R_{emp}\left(f\right)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)$$
• 经验风险最小化与结构风险最小化
  • 经验风险最小化（ERM）
    当样本容量足够大时，经验风险最小化能保证有很好的学习效果，也就是求解最优问题：
    $$\underset{f\in \mathcal{F}}{\min }\frac{1}{N}\sum _{i=1}^{N}L\left(y_i|f\left(x_i\right)\right)$$
    极大似然估计就是经验风险最小化的一个例子。
    但样本过小就会导致“过拟合”。
  • 结构化风险最小（SRM）
    为了防止过拟合而提出的策略。结构化风险在经验风险的基础上增加了模型复杂度的正则化项（或罚项）。因此定义为：
    $$R_{srm}\left(f\right)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)+\lambda J\left(f\right)$$
    其中$J\left(f\right)$为模型复杂度，越大函数越复杂；$\lambda \ge 0$是系数用来权衡经验风险和模型复杂度。
    贝叶斯估计中的最大后验概率估计就是结构风险最小化的例子。

算法

在确定了训练数据集、学习策略并从假设空间中选择最有模型的基础上，需要考虑使用什么算法求解最优模型。

模型评估与模型选择（一）

训练误差与测试误差

假设学习得到的算法是$Y=\hat{f}(X)$

• 训练误差：是算法在训练集上的平均损失$$R_{emp}\left(\hat{f}\right)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,\hat{f}\left(x_i\right)\right)$$
• 测试误差：算法在测试集上的平均误差$$e_{test}\left(\hat{f}\right)=\frac{1}{N^{\prime }}\sum _{i=1}^{N^{\prime }}L\left(y_i,\hat{f}\left(x_i\right)\right)$$
• 测试误差率：当损失函数为0-1损失时，测试误差变为误差率，记为$$e_{test}=\frac{1}{N^{\prime }}\sum _{i=1}^{N^{\prime }}I\left(y_i̸=\hat{f}\left(x_i\right)\right)$$
  其中$I$为指示函数，$y̸=\hat{f}(x)$时为$1$，否则为$0$。
• 测试准确率：$r_{test}=1-e_{test}$

过拟合、欠拟合与模型选择

模型的选择应该是以真实情况作为依据，也就是逼近所谓的“真模型”，而不应该只追求模型在训练集上的表现效果。

• 过拟合与欠拟合
  首先看个实际得实例：
  
  • 过拟合
    一味追求提高对训练集的预测能力（学习了训练样本中存在得特点），模型过于复杂，往往复杂度高于“真模型”。
    特点：对于已知数据表现很好，对于未知数据表现很差。
  • 欠拟合
    欠拟合相对比较好理解，就是指对训练样本得一般性质未能学好。
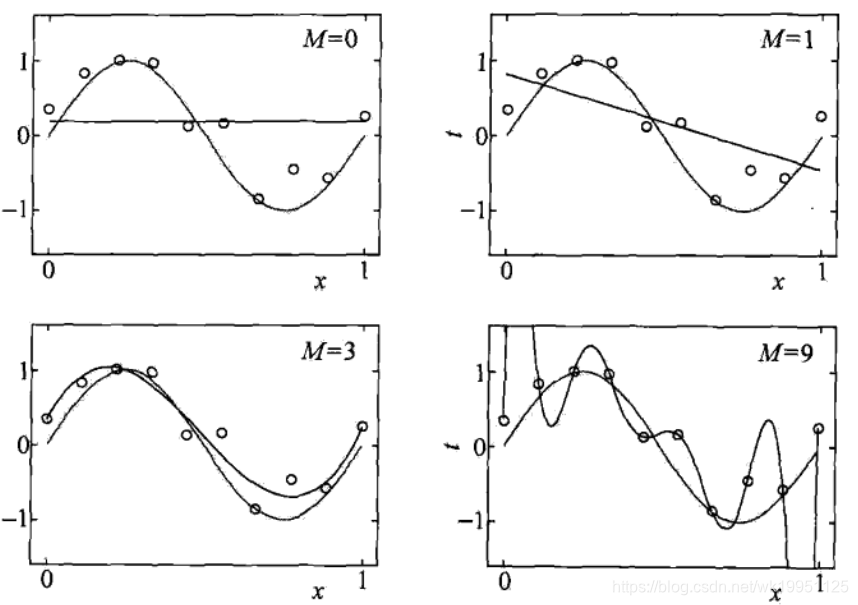
    下图从另一个角度展示了一个过拟合的与欠拟合（M表示多项次的次数），可以很显然得发现：
  1. 当$M=0$时，完全就是一条与$x$轴平行的直线，并没有学习到什么有用得信息；
  2. 当$M=1$时，直线发生了一定的倾斜，但其实也与“真模型”相差甚远，此时仍处于“欠拟合”的状态。
  3. 当$M=9$时，图像经过了所有已知点，但是图像非常复杂且偏离“真模型”，可以想象其用来预测也会导致很差得结果。
     
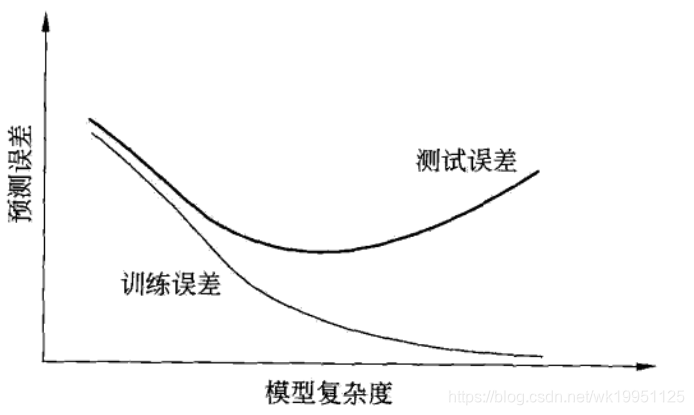
     下图也给出了随着模型复杂度的变化，训练误差与测试误差的变化情况。
     

参考文献

• 《统计学习方法》
• 《机器学习》