蓝桥杯--历届真题 移动距离【第六届】【省赛】【B组】

试题 历届真题 移动距离【第六届】【省赛】【B组】

提交此题   评测记录  

资源限制

时间限制：1.0s   内存限制：256.0MB

　　X星球居民小区的楼房全是一样的，并且按矩阵样式排列。其楼房的编号为1,2,3...
　　当排满一行时，从下一行相邻的楼往反方向排号。
　　比如：当小区排号宽度为6时，开始情形如下：

　　1 2 3 4 5 6
　　12 11 10 9 8 7
　　13 14 15 .....

　　我们的问题是：已知了两个楼号m和n，需要求出它们之间的最短移动距离（不能斜线方向移动）

　　输入为3个整数w m n，空格分开，都在1到10000范围内
　　w为排号宽度，m,n为待计算的楼号。
　　要求输出一个整数，表示m n 两楼间最短移动距离。

　　例如：
　　用户输入：
　　6 8 2
　　则，程序应该输出：
　　4

　　再例如：
　　用户输入：
　　4 7 20
　　则，程序应该输出：
　　5

　　资源约定：
　　峰值内存消耗 < 256M
　　CPU消耗 < 1000ms

 

 

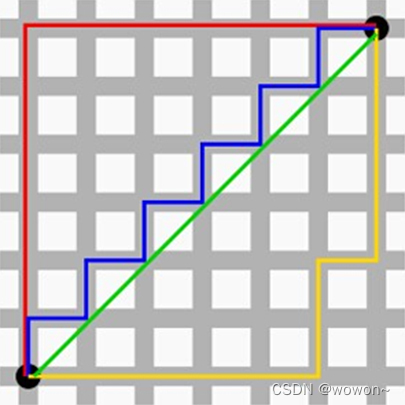
图1 曼哈顿距离
图1中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离， 即

d(i,j)=|xi-xj|+|yi-yj|

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int w,m,n;
    cin>>w>>m>>n;
    m--;
    n--;//序号都减一，因为要套公式
    
    int x1=m/w;
    int y1=m%w;
    
    int x2=n/w;
    int y2=n%w;
    
    if(x1&1)//如果x1是奇数
    y1=w-1-y1;
    if(x2&1)
    y2=w-1-y2;
    
    cout<<abs(x1-x2)+abs(y1-y2)<<endl;
    
    
    return 0;
}