1219. 移动距离 Java 题解 （模拟）【第六届蓝桥杯省赛C++B组,JAVA A/C组】

输入样例：

6 8 2

输出样例：

4

---

解题思路：

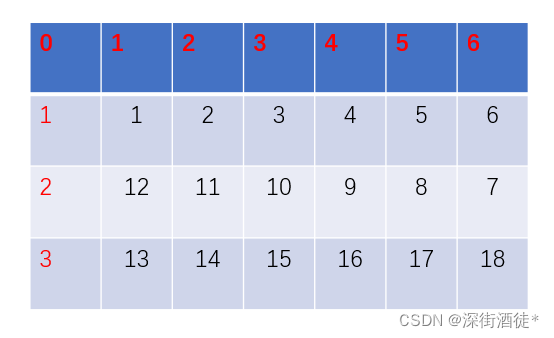
 可以将数组中的元素把零行零列空出来存入二维数组中，并找出楼层号，两数的横纵坐标差就是所求的距离，时间复杂度为O(N)，N = max(m,n)

 

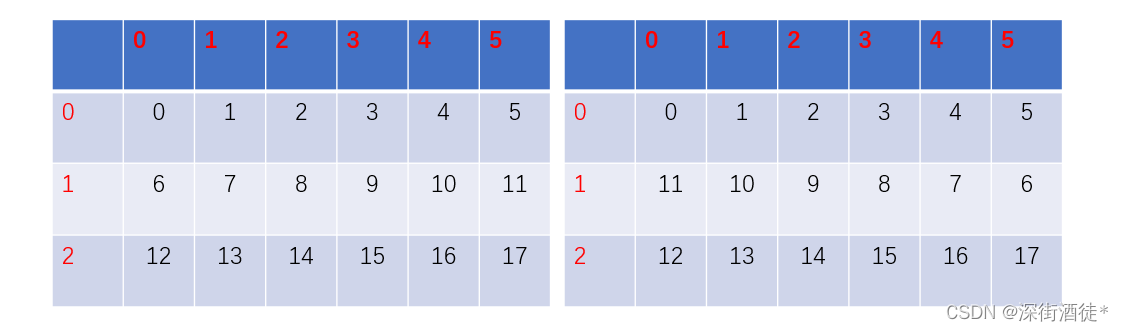
可以利用数组的下标规律直接求解：当空出[0][0]元素时，实际的楼号就相当于在原基础上加一，在计算时两数各减一的相对距离就是答案。而此时的每个数的行索引就等于n/6，列索引为n%6，但当基数行时，需要将列索引“翻转”，最后两坐标相差即为答案。时间复杂度为O(1)。

Java代码：O(n)

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int w = scan.nextInt();
		int m = scan.nextInt();
		int n = scan.nextInt();
		scan.close();
		int [][] map = new int[10001 / w + 5][w + 1];
		
		int max = Math.max(m, n);//找最大的楼号数
		int j = 1, row = 1;
		while(j < max) {
			for(int i = 1; i <= w; i++) {//正序排列
				map[row][i] = j;
				j++;
			}
			row++;
			for(int i = w; i >= 1; i--) {//逆序排列
				map[row][i] = j;
				j++;
			}
			row++;
		}
		
		@SuppressWarnings("unused")
		int indexAx = 1, indexAy = 1;//m楼的索引
		@SuppressWarnings("unused")
		int indexBx= 1, indexBy = 1;//n楼的索引
		int flag = 0;//标志是否已经找到两栋楼
		for(int i = 1; i <= map.length; i++) {
			for(j = 1; j <= w; j++) {
				if(map[i][j] == m) {
					indexAx = i; 
					indexAy = j;
					flag++;
				}
				if(map[i][j] == n) {
					indexBx = i; 
					indexBy = j;
					flag++;
				}
			}
			if(flag == 2) break;
		}
		System.out.println((int)Math.abs(indexBy - indexAy) + (int)Math.abs(indexAx - indexBx));
	}
}

Java代码：O(1) 

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int w = scan.nextInt();
		int m = scan.nextInt() - 1;//找相对位置
		int n = scan.nextInt() - 1;
		scan.close();
		
		int x1 = m / w;
		int x2 = n / w;
		int y1 = m % w;
		int y2 = n % w;
		if(x1 % 2 == 1) y1 = w - 1 - y1;
		if(x2 % 2 == 1) y2 = w - 1 - y2;
		System.out.println(Math.abs(x1 - x2) + Math.abs(y1 - y2));
	}
}