模板生成系统
来源:CCF
标签:
参考资料:
相似题目:
题目
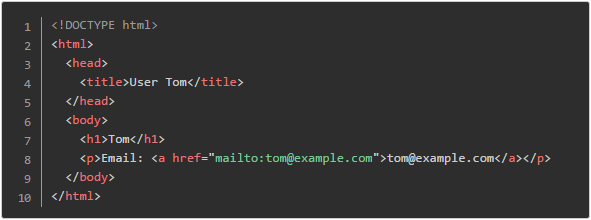
成成最近在搭建一个网站,其中一些页面的部分内容来自数据库中不同的数据记录,但是页面的基本结构是相同的。例如,对于展示用户信息的页面,当用户为 Tom 时,网页的源代码是
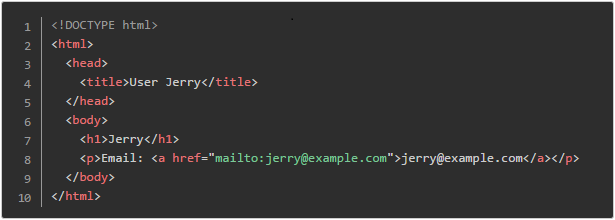
而当用户为 Jerry 时,网页的源代码是
这样的例子在包含动态内容的网站中还有很多。为了简化生成网页的工作,成成觉得他需要引入一套模板生成系统。
模板是包含特殊标记的文本。成成用到的模板只包含一种特殊标记,格式为 { { VAR }},其中 VAR 是一个变量。该标记在模板生成时会被变量 VAR 的值所替代。例如,如果变量 name = “Tom”,则 { { name }} 会生成 Tom。具体的规则如下:
·变量名由大小写字母、数字和下划线 (_) 构成,且第一个字符不是数字,长度不超过 16 个字符。
·变量名是大小写敏感的,Name 和 name 是两








 本文介绍了CCF计算机软件能力认证中的一道试题,涉及模板生成系统。模板包含{{ VAR }}标记,用于替换变量VAR的值。题目提供模板的行数、变量个数,以及每个变量及其值,输出是生成后的模板结果。题目对变量名和值的格式有特定限制,并给出了输入输出样例及参考代码。
本文介绍了CCF计算机软件能力认证中的一道试题,涉及模板生成系统。模板包含{{ VAR }}标记,用于替换变量VAR的值。题目提供模板的行数、变量个数,以及每个变量及其值,输出是生成后的模板结果。题目对变量名和值的格式有特定限制,并给出了输入输出样例及参考代码。

 订阅专栏 解锁全文
订阅专栏 解锁全文


















 2300
2300

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










