【计算机图形学】图元的扫描转换之圆的扫描转换

相关资料来源于网络，侵删歉。
如果文章中存在错误，请下方评论告知我，谢谢！

---

圆的扫描转换

前提
1.圆心在原点
2.半径R为整数

首先我们直接可以想到这种方法，由圆的方程 ，得到。那么给定一个范围的x，每一个x对应一个y，圆就被绘制出来了。但是，这种方法效率很低，平方计算，开平方计算，还需要对x、y取整，点分布不均匀，如下图。

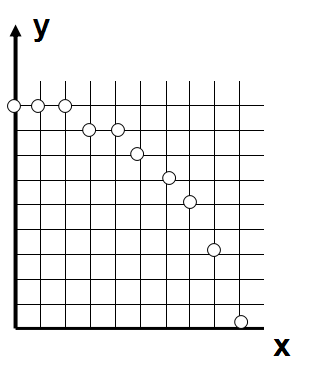
接下来我们又想到，由圆的参数方程，x=Rcosθ，y=Rsinθ，θ从0到90度，得到1/4圆，可由对称性得到完整的圆。这种方法减小了点的分布不均匀，但是效率仍然很低，因为涉及浮点运算，乘法运算，取整运算。这种方法能否改进呢？

八方向对称性
由圆的多种对称，只需要圆上一点，我们就可以找到圆上的另外7个点，如图。为此，我们计算一个45度的圆弧就可以得到完整的圆。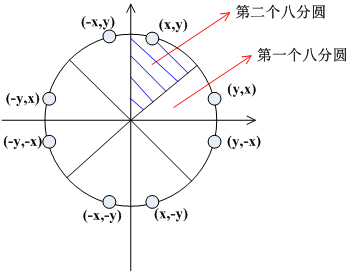

中点圆算法
（注：这种思想与直线的扫描转换类似，如果不理解请先阅读那篇文章。）
我们考虑第二个八分圆，P点为已点亮像素，那么下一个要点亮的像素是E或者SE，如图。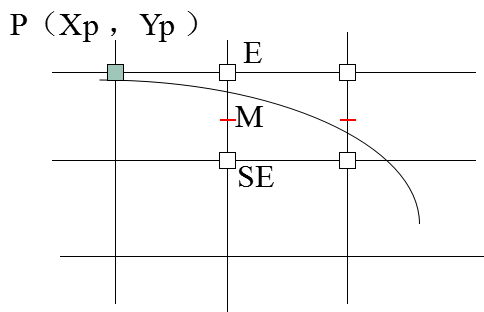

构造函数，存在三种情况：
如果F(x,y)=0，那么点在圆上；
如果F(x,y)>0，那么点在圆外；
如果F(x,y)<0，那么点在圆内。

取E和SE的中点M，将M点代入F(x,y)，根据符号可判断M点与圆的位置关系。
当F(x,y)>0时，M点在圆外，弧线离SE更近，应取SE点；
当F(x,y)<0时，M点在圆内，弧线离E点更近，应取E点；
当F(x,y)=0时，M点在圆上，取SE和E都行。（当连续的M点总是在圆上时，应总是取SE或E的其一）
但是，直接代入存在浮点运算，平方运算，效率较低。我们仍然采用增量算法来优化。

我们由P点可以推出M点的坐标，再由M点的坐标可以推出下一个中点M'的坐标。
令
当d<0，即M点在弧线下方，此时取E点，下一个中点M'的坐标为，如图。（请自行考虑为什么是M'点）


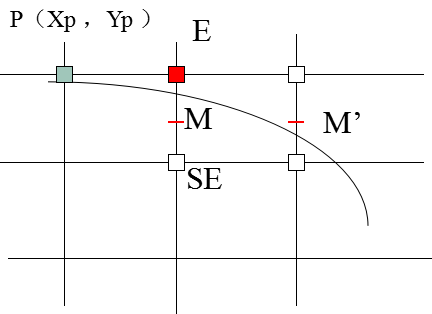
比较得知，M点与M'点代入F(x,y)相差2xp+3，即增量为2xp+3。

当d=0，即M点在弧线上，此时取E和SE皆可，这里取SE点。
当d>0，即M点在弧线上方，此时取SE点，下一个中点M'的坐标为，如图


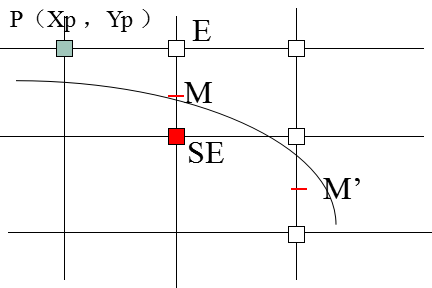
比较得知，M点与M'点代入F(x,y)相差2(xp-yp)+5，即增量为2(xp-yp)+5。

综上：
当中点M在弧线下方时，即d<0，取E点，下一个要判断的是d+2xp+3的符号。
当中点M在弧线上或上方时，即d>=0，取SE点，下一个要判断的是d+2(xp-yp)+5的符号。
然后再根据符号取E点或者SE点。

在实现算法前，我们需要知道P的初始坐标P0，和d的初值d0。
我们从(0,R)点开始画圆，所以P0点坐标为(0,R)，则
因为我们只需要判断d的符号，为了效率，我们将d0乘以4得5-4R，去除浮点数，同样，我们也需要将上面讨论的增量乘以4，得8xp+12，8(xp-yp)+20。

实现（这里只给出基础算法，具体的[待编写]）

void MidpointCircle(int R, int color){
	int x,y,d;
	x=0;y=R; 
	d=5-4*R;
	WritePixel(x,y,color);
	while(x<y){
		if(d<0){
			d+=8*x+12;
			x++; 
		}
		else{
			d+=8*(x-y)+20;
			x++;
			y--;
		}
		WritePixel(x,y,color);
	}
}

认真考虑后发现，其实我们没必要乘4。
d=1.25-R，设h=d-0.25=1-R，那么d=h+0.25。我们之前在比较d与0的关系，现在只要比较h与-0.25的关系。由于h是整数，所以只要比较h与0的关系即可。有一点需要注意，当h=0时，比较h与-0.25的关系，h>-0.25，但是现在比较h与0的关系，h=0，即使这样，也不影响结果。

MidpointCircle(int R, int color){
	int x,y,h;
	x=0;y=R; 
	h=1-R;
	WritePixel(x,y,color);
	while(x<y){
		if(h<0){
			h+=2*x+3;
			x++; 
		}
		else{
			h+=2*(x-y)+5;
			x++;
			y--;
		}
		WritePixel(x,y,color);
	}
}