【计算机图形学】图元的扫描转换之直线的扫描转换

最新推荐文章于 2023-11-29 14:00:09 发布

原创最新推荐文章于 2023-11-29 14:00:09 发布 · 4.3k 阅读

19 ·

CC 4.0 BY-SA版权

本文为博主原创文章，未经博主允许不得转载。

温故知新专栏收录该内容

116 篇文章

订阅专栏

相关资料来源于网络，侵删歉。
如果文章中存在错误，请下方评论告知我，谢谢！

直线的扫描转换

定义：直线的扫描转换是指在二维栅格上计算位于该直线上或充分靠近它的一串像素坐标(光栅化)，并以此像素集近似替代原连续直线段在屏幕上显示的过程。直线由两个端点坐标确定。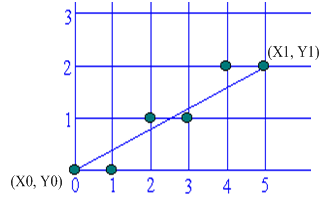

要求
1.观感好,像素分布均匀
2.误差小,像素尽可能接近数学理想坐标
3.速度快，避免乘除法和浮点数运算

前提
线的宽度是一个像素
线的端点是整数坐标
直线斜率|k|<=1

原理
按直线从起点到终点的顺序计算直线与各垂直光栅网格线的交点，然后确定每列像素中与此交点最近的像素。

基本增量算法（DDA）

已知过端点 $P_{0}(x_{0},y_{0})$ ， $P_{1}(x_{1},y_{1})$ 的直线段L： $y=kx+b$ 。从直线左端点开始，x每次递增1个单位，对 $x_{i}$ 计算 $y_{i}=kx_{i}+b$ 。显示坐标为 $(x_{i}, floor(y_{i}+0.5))$ 的像素（注意：四舍五入）。这种方法直观，但效率太低，因为每一步需要用浮点计算一次乘法、一次加法和一次取整运算。我们对此稍微改进，去掉其中的乘法。由于 $y_{i+1}=kx_{i+1}+b=k(x_{i}+1)+b=y_{i}+k$ ，所以每次x递增一个单位，y就加上一个k。（如果线的斜率在1和-1之间（包括1和-1），则每一列上必定只有一个像素被显示；若线的斜率在此范围之外，则每一行上必定只有一个像素被显示。如果|k|>1，我们将x和y的角色互换，即y每次增加一个单位，x变化的增量为1/m。）

实现（这里只给出基础算法，具体的[待编写]）

/*
	基本增量算法
	适用于直线斜率k在[-1,1]的情况。
*/
void Line(int x0,int y0,int x1,int y1,int color){
	int x;
	double dy=y1-y0;
	double dx=x1-x0;
	double k=dy/dx;
	double y=y0;
	for(x=x0;x<=x1;x++){
		WritePixel(x,floor(y+0.5),color);
		y+=m;
	}
}

上述程序的缺点是：对y值取整需要发费时间，且y和k是浮点数，存在浮点运算。

中点线算法

假定直线斜率0<k<1，且已确定点亮像素点 $P(x_{p}, y_{p})$ ,则下一个与直线最接近的像素可能是其右边的第一个像素E(称为东像素)，也可能是其右上方的第一个像素NE(称为东北像素) 。假设Q是直线与栅格线 $x=x_{p}+1$ 的交点，M为E和NE的中点。

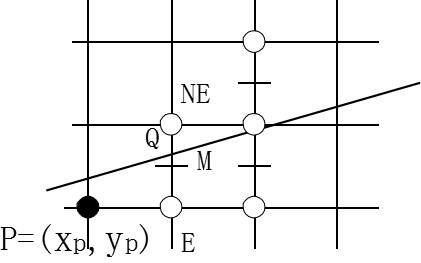
当M在Q的上方时，Q离E更近，取E；
当M在Q的下方时，Q离NE更近，取NE；
当M与Q重合时，NE或E任取。（如果总是重合，应该总是取NE或E中的其一）

下面需要判断Q与M的关系：
设直线方程为F(x,y)=ax+by+c=0，(注意：a>0)
当F(x0,y0)<0，(x0, y0)在直线的上方
当F(x0,y0)>0，(x0, y0)在直线的下方
当F(x0,y0)=0，(x0, y0)在直线上

那么由已知点P推出M点代入直线方程根据符号即可判断。
$F(x_{M},y_{M})=F(x_{P}+1,y_{P}+0.5)=a(x_{P}+1)+b(y_{p}+0.5)+c$
但效率不高，因为存在浮点数乘法运算。下面我们由增量算法对此改进。

令 $d=F(x_{M},y_{M})=F(x_{P},y_{P})+a+0.5b$ ，对d的符号分类讨论，从而推出下一个M点：

如果d>0，M点在直线下方，取NE点；
如果d=0，M点在直线上，NE和E任取，这里同样取E点。
下一个要研究的中点应是M'点，如下图（至于为什么是M'点，而不是其上的中点，请自行考虑）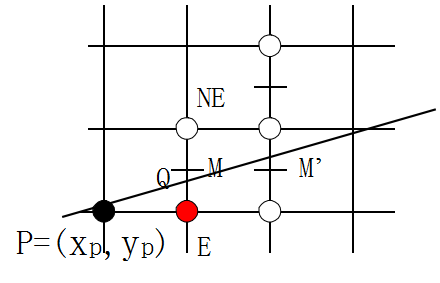

$F(x_{M'},y_{M'})=F(x_{P}+2,y_{P}+0.5)=F(x_{P},y_{P})+2a+0.5b=d+a$
比较得知，M与M'点代入直线方程，两者相差a，即增量为a。

如果d<0，M在直线上方，取E点，此时下一个中点为M'点，如下图。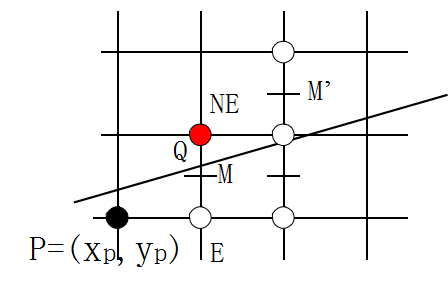

$F(x_{M'},y_{M'})=F(x_{P}+2,y_{P}+1.5)=F(x_{P},y_{P})+2a+1.5b=d+a+b$
比较得知，M与M'点代入直线方程，两者相差a+b，即增量为a+b。

综上：
如果中点M(x,y)在直线上或在直线上方，即d<=0，取E点，下一个要判断的是d+a的符号。
如果中点M(x,y)在直线下方，即d>0，取NE点，下一个要判断的是d+a+b的符号。
然后再根据符号取NE点或者E点。

算法实现前，我们还需要计算a，b，这个由直线起点(x0,y0)和终点(x1,y1)得到，a=y1-y0，b=x0-x1
因为第一个像素就是直线的起点(x0,y0)，F(x0,y0)=0，所以d的初值为 $F(x_{0}+1,y_{0}+0.5)=F(x_{0},y_{0})+a+0.5b=a+0.5b$
由于我们只需要判断符号，并且减少浮点运算，所以我们将d*2，得到 $d_{0}=2a+b$
同样，上面的增量也需要乘以2，即2a，2(a+b)。

实现（这里只给出基础算法，具体的[待编写]）

/*
    适用于斜率k在[0,1]的直线
*/
void MidpointLine(int x0, int y0, int x1, int y1, int color){
	int dx=x1-x0;
	int dy=y1-y0;
	int d=2*dy-dx;//d的初始值
	int incrE=2*dy;//选择E点时所用的增量
	int incrNE=2*(dy-dx);//选择NE点时所用的增量
	int x=x0;
	int y=y0;
	
	WritePixel(x,y,color);
	while(x<=x1){
		if(d<=0){//选择E点
			d+=incrE;
			x++;
		}
		else{//选择NE点
			d+=incrNE;
			x++;
			y++;
		}
		WritePixel(x,y,color);
	}
}