基于神经电路的并行排序系统

基于离散时间神经电路模型的并行排序系统设计

摘要

设计了一种基于离散时间K胜者为王（KWTA）神经电路（NC）模型的并行排序系统。该系统由一组差分方程和阶跃函数描述。离散时间KWTA神经电路（NC）模型由差分方程和阶跃函数给出。文中给出了相应的系统功能框图。定义了排序过程收敛至稳态所需迭代次数的上限。该系统无需知晓输入数据变化范围。为了使用该系统，应已知输入之间的最小差异。该系统适用于处理位于任意未知有限范围内、具有有限值的未知输入。该系统具有任意有限的输入分辨率、高速度、适中的计算复杂度以及软件实现复杂度。提供了计算机仿真结果以说明该系统的高效性。

1. 引言

排序是将输入数据按升序序列、降序序列、字母顺序序列等进行排列的操作。超过25%的计算时间用于排序。排序操作广泛应用于数据和信号处理、通信、导航、移动设备、人工智能、超大规模集成电路设计等领域[1]。因此，设计高效的排序算法以最小化排序的时间和存储空间是一个极为重要的问题。

已应用多种串行排序方法[1]。如果需要对大量数据进行排序，串行排序算法可能效率不足，因为它们具有二次计算复杂度$\Theta(N^2)$。因此，此种情况下可采用具有线性计算复杂度$\Theta(N)$的并行排序算法。各种并行排序算法和架构在文献[2]中有所描述。基于连续时间神经网络（NNs）的并行排序系统应用于[3]–[10]及其中引用的参考文献中。使用超大规模集成电路技术实现排序系统的硬件示例见[8],[9]。

离散时间神经网络更准确、可靠，更适合处理实际噪声数据。这类网络在并行软件中实现更为方便。此外，它们还可以在最新的并行数字硬件[11]中实现。

让我们基于[12]中提出的离散时间神经电路（NC）模型设计一个并行排序系统。该系统应具备输入数据的任意有限高分辨率、高速数据处理能力以及线性计算复杂度。此外，该系统应具有适中的硬件实现复杂度，并能够处理位于任何有限未知范围内的有限未知输入数据。应提供计算机仿真以验证理论推导。

2. 基本离散时间神经电路

考虑一个向量$a = (a_1, a_2, …, a_N)^T$，由实输入数据组成，其元素的值未知。这些输入是互异且有限的，即
$$
a_i \neq a_j, \quad -\infty < a_i, a_j < \infty, \quad i \neq j, \quad i,j = 1,2,…,N
$$
其中文中提出的简单且快速的离散时间K‐胜者为王（KWTA）神经电路[12]能够确定这些输入中最大的K个值，这些值被称为胜者。具体而言，该电路处理这些输入的向量$a$，以得到一个相应的输出向量$b = (b_1, b_2, …, b_N)^T$，使得满足以下KWTA特性：
$$
b_i > 0, \quad i = 1,2,…,K; \quad b_j < 0, \quad j = K+1,…,N
$$

简化在[12]中描述的神经电路，其由以下差分方程表示：
$$
y(l+1) = y(l) + r \cdot \text{sgn}(D(y))
$$
其中$y(l)$是具有初始条件的离散时间状态变量，$D(y)$是获得的正输出数与所需正输出数之间的差值函数，
$$
D(y) = K - \sum_{k=1}^{N} S(y_k), \quad S(y_k) =
\begin{cases}
1, & \text{if } y_k > a_k \
0, & \text{otherwise}
\end{cases}
$$
是一个阶跃函数，
$$
\text{sgn}(D(y)) =
\begin{cases}
1, & \text{if } D(y) > 0 \
0, & \text{if } D(y) = 0 \
-1, & \text{if } D(y) < 0
\end{cases}
$$
是符号函数，$r$是一个参数，其值应小于输入间的最小差值，即需满足不等式$r \leq \min_{i \neq j} |a_i - a_j|$，$i,j = 1,2,…,N$。达到搜索过程收敛至稳态KWTA操作所需的迭代次数上限如下所示：
$$
m^ \leq \frac{|y^ - y(1)|}{r}
$$
其中$y^*$是$y(l)$的稳态值。可以看出，由差分方程(3)和输出方程(4)描述的神经电路需要设置一个参数值，该值应小于输入间的最小差值。这意味着输入间的最小差值必须已知。

3. 基于神经电路的离散时间并行排序系统模型

在并行排序中，排序顺序可以表示为一个置换矩阵。在这种矩阵中，“1”位于标记为$i$的行和标签为$j$的位置，可确定为无序列表中的第$i$项和有序列表中的第$j$项[8]–[10]。例如，在$i=1,2,…,10$的情况下，输入的无序列表${a_1,a_2,…,a_{10}}$及其有序列表${d_1,d_2,…,d_{10}}$由以下对应的置换矩阵描述：

矩阵(7)可以转换为给定的排序矩阵：

一般情况下，排序结果可以表示如下：
$$
d_1 = a^T S_1, \quad d_{K+1} = a^T (S_{K+1} - S_K), \quad K = 1,2,…,N-1
$$
其中，$S_K = [S_{K1}, S_{K2}, …, S_{KN}]^T$，$K=1,2,…,N-1$的排序矩阵元素由差分方程(3)使用阶跃函数(4)确定。

由于$S_1 = [1,1,…,1]^T$，$S_N = [1,1,…,1]^T$，仅需$N-1$个方程（3），每个方程从左到右计算排序矩阵的一列，其中$k$从1增加到$N-1$。因此，与其他使用$N-1$个神经元的排序系统相比，仅需$\frac{N^2}{2}$个neurons[9]。具体而言，1WTA网络用于确定列表中的最大元素。在并行模式下无需重新计算第一项时，需要1WTA网络和2WTA网络来计算列表中的第二项。在并行模式下无需重新计算第二项时，需要2WTA网络和3WTA网络来确定列表中的第三项，依此类推。因此，通过使用KWTA网络，N个项目的整个列表可被排序，其中$K=1,2,…,N-1$，且无需计算最后一项，只需设置$S_N = [1,1,…,1]^T$[3],[8]。

4. 系统的功能框图

由差分方程(3)和输出方程(4)描述的离散时间NC的功能框图如图1(a)所示。图1(b)给出了由(9)式中第一个方程描述的部分并行排序系统的功能框图。由(9)式中第二个方程描述的部分并行排序系统的功能框图如图1(c)所示。这些框图包括输入、加法器$\sum$、阶跃函数模块$S(y_k)$，$k=1,2,3,…,N$、符号函数$\text{sgn}(5)$、乘法器、时间延迟、恒定信号外部源以及输出。

)

(a)

)

(b)

)

(c)

图1。（a）由差分方程(3)和输出方程(4)描述的离散时间NC的功能框图；（b）基于由公式(9)的第一个方程描述的NN的并行排序系统部分的功能框图；（c）基于由公式(9)的第二个方程描述的NN的并行排序系统部分的功能框图。

图1(a)所示的框图包含一个乘法器、一个时间延迟单元、三个恒定信号源（如果+1则为两个恒定信号源）、N个受控开关以及N个加法器。图1(b)所示的框图包含N个乘法器和一个加法器。图1(c)所示的框图包含N个乘法器和N个加法器。

基于连续时间KWTA神经网络并采用海维赛德阶跃激活函数和单状态变量的最简单比较型离散时间并行排序系统之一的功能框图，如[10]中所述，该系统以类似方式应用于并行排序，需要一个恒定信号、一个积分器、N个开关和N+1个加法器。因此，从复杂性的角度来看，基于由差分方程(3)和输出方程(4)描述的神经电路的离散时间并行排序系统与其他类似的系统相近。

图1中所示的功能框图可以实现在并行软件或并行数字超大规模集成电路硬件中。如果需要精确、简单且灵活的并行实现，则可优先选择软件实现。如果需要快速、紧凑、可靠且抗噪声的实现，则可将这些功能框图实现在数字硬件中[13]。

5. 系统的计算机仿真

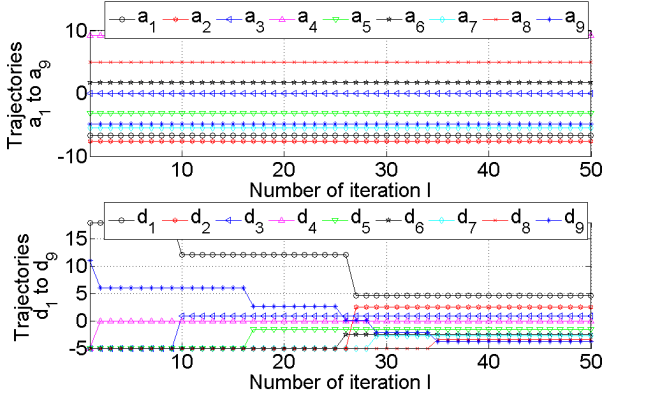
考虑一个计算机仿真的示例，用于展示由方程(3)、(4)和(9)描述的离散时间并行排序系统的性能。让我们使用由方程(3)、(4)和(9)描述的并行排序系统对区间(-10.0, 10.0)上均匀分布的九个元素的随机数进行排序。我们设定离散时间状态变量的初始值为$y_k(1) = 0.5$，$k = 1,2,…,N$。通过由差分方程(3)、(4)和(9)描述的八个神经电路，我们仅需八个神经元，而不像81个神经元那样用于[9]中的模拟排序网络。

图2. 并行排序系统的输出轨迹，该系统由方程(3)、(4)和(9)描述，其中N=9在区间(-10.0,10.0)上均匀分布的随机输入$a$,$r=0.01$，和$y_k(1)=0.5$，$k=1,2,…,N$。

图3：由方程(3)、(4)和(9)描述的并行排序系统在不同离散时间状态变量初始值（取值区间为(-10.0,10.0)）下实现并行排序所需的最大迭代次数。

从仿真结果可以看出，由方程(3)、(4)和(9)描述的并行排序系统具有高精度和快速性。此外，该系统不需要知道输入的变化范围。为了使用该系统，像[10]中提出的接近的离散时间比较模拟一样，只需知道输入间的最小差值即可。然而，与由方程(3)、(4)和(9)描述的并行排序系统相比，这种模拟在输入数量较多且输入间最小差异较小时，需要在描述离散时间KWTA NN模型的差分方程右侧将大数值的差值函数乘以小数值的参数。这可能导致出现误差，进而引起此类并行排序系统的错误操作。此外，上述乘法运算在相应硬件中可能难以实现。

提出结论了用于对位于未知有限变化范围内的任意未知有限输入进行离散时间并行排序的系统及其相应的功能框图。该系统具有高运行速度和对输入的任意有限分辨率。系统的实际运行速度和分辨率受限于其软件或硬件实现的限制。该系统可实现在并行软件或并行数字超大规模集成电路硬件中。当需要精确、简单且灵活的并行实现时，可选择软件实现方式。当需要快速、可靠且抗噪声干扰的并行实现时，可采用数字硬件实现。通过计算机仿真验证了该系统在快速而精确的并行排序中的高性能。当需要对大量具有已知最小差异、位于未知有限变化范围内的未知有限输入以高分辨率和高速度进行排序时，推荐使用该系统。