PyTorch|简单实现线性回归模型

最新推荐文章于 2025-10-21 15:38:58 发布

原创

最新推荐文章于 2025-10-21 15:38:58 发布 · 1.8k 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#pytorch #线性回归 #python

01 | 什么是线性回归？

线性回归是分析一个变量与另外一个（或多个）变量之间关系的一种方法，该方法需要从实际数据中抽象出因变量Y、自变量X，且假定Y相对于X按照近似线性的方式变化，即函数图像上近似呈现一条直线。通常可以用下述公式表示，而模型求解目标为确定其中的斜率W与偏置b。

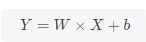
在这里插入图片描述

线性回归的求解过程一般分为三步：

确定模型，对于我们而言即确定模型求解目标是确定W与b
选择损失函数作为优化迭代目标，本例中选用常用的均方误差指标（MSE），即模型预测值与真实值差的平方和均值，用公式表示即:
最后就是求解MSE中相对于W与b的梯度并更新W与b，以获得较小MSE时的最优参数数值。

02 | PyCharm下的PyTorch代码

# 借助PyTorch实现一个简单的线性回归模型 
import matplotlib.pyplot as plt 
import torch 

torch.manual_seed(10) #设定随机数种子 
lr = 0.1 # 学习率 

# 创建训练集 
x = torch.rand(20, 1) * 10 # 创建一个（20,1）的Tensor，每个数值扩大10倍（默认小于1） 
y = 2*x + (6 + torch.randn(20, 1)) # 近似线性公式，模拟随机噪声