新型三维混沌系统及其控制

一种新的三维混沌系统：其自适应控制与电路设计

1 引言

表现出混沌运动的非线性动力系统在科学与工程中具有多种应用（Azar 和 Vaidyanathan，2016；Vaidyanathan 和 Volos，2016）。基于混沌的控制系统已为许多工程应用所设计（Azar 等，2017；Vaidyanathan 和 Volos，2017）。具体而言，混沌理论的应用包括急动机械系统（Rasappan 和 Vaidyanathan，2012；Vaidyanathan 等，2015b；Vaidyanathan，2015c）、振荡器（Vaidyanathan 等，2015a； Vaidyanathan，2015f，2015e；2012；Vaidyanathan 和 Rasappan，2011； Pakiriswamy 和 Vaidyanathan，2012）、化学混沌反应器系统（Vaidyanathan，2015b）、神经元（Vaidyanathan，2015a，2015d）、神经网络（Vaidyanathan，2015g）、电路（Pham 等，2016；Volosetal., 2017）等。目前存在显著的研究兴趣在工程自动化与控制领域（Thabet 等，2017；拉赫塔拉和艾哈迈迪，2017；罗伊等人，2017；郭和董，2017；基德等人，2017；何等人，2017；萨兰吉等人，2017；佩鲁马尔和格纳南巴尔，2017；贝纳萨尔等人，2017；瓦伊迪亚纳坦等人，2018）。

谢等人（2015）讨论了具有外部扰动的金融混沌系统的函数投影同步。塔查等人（2016）提出了一种新的金融混沌系统，该系统是复杂经济系统的模型，并讨论了其基于自适应控制理论的控制方法。格里特利和贝尔希特（2016）通过基于OGY的控制研究了被动指南针步态模型的行走动力学。阿尔‐苏海尔等人（2018）推导出了用于反隐身应用的长波混沌雷达系统的新成果。纪等人（2018）提出了一种新型分数阶逻辑混沌映射，并在其研究中讨论了新的分岔类型和混沌现象。王等人（2018）提出了一种用于离散余弦变换（DCT）预编码正交频分复用（OFDM）可见光通信（VLC）系统的双层图像加密方案。

张等人（2015）宣布了一种使用沃尔什码的新型混沌保密通信系统。霍拉萨迪扎德和马吉迪（2017）利用傅里叶级数展开实现混沌同步，并将其应用于保密通信系统。扎莫勒等人（2017）研究了基于新型Beta混沌映射的混沌序列在图像加密中的应用问题。古福（2017）讨论了具有三维四涡卷吸引子的混沌分数阶系统的可解性。瓦伊迪亚纳坦等人（2018）提出了一种具有两个二次非线性的新型四维超混沌系统，并通过李雅普诺夫稳定性理论讨论了其自适应同步。王等人（2017）提出了一种具有超混沌吸引子的新超跃变系统，并设计了其电子电路。瓦伊迪亚纳坦等人（2017）采用反步控制法实现了具有未知参数的相同新颖跃变混沌系统的全局混沌同步，并讨论了其在语音加密中的应用。瓦伊迪亚纳坦和里夫（2017）描述了一种新型三维四叶混沌系统，并通过积分滑模控制讨论了其自适应控制。

在本研究中，我们提出了一种具有两个非线性项的新三维混沌系统，即一个二次非线性和一个四次非线性。展示了该新混沌系统的相图，并讨论了其对称性、耗散性、平衡点、李雅普诺夫混沌指数和Kaplan‐Yorke分形维数等定性性质。

作为控制应用，我们推导了针对具有未知系统参数的新混沌系统的自适应稳定化和同步的新结果。我们的自适应控制结果是在系统参数无法用于测量的一般情况下推导得出的。此外，我们还展示了电子电路实现，以验证该新混沌系统的可行性。

2 一个新的混沌系统

我们提出了一种具有两个非线性项的新三维系统，其表达式为

$$
\begin{cases}
\dot{x}_1 = a(x_2 - x_1) \
\dot{x}_2 = x_1x_3 \
\dot{x}_3 = 50 - bx_1^4 - cx_3
\end{cases}
\quad (1)
$$

值得注意的是，系统 (1) 在第一个方程中包含线性项，第二个方程中包含二次非线性 $(x_1x_3)$，第三个方程中包含四次非线性 $(x_1^4)$。

我们确定当参数取值为$(a, b, c) = (3, 1, 1)$时，系统(1)描述了一个自激混沌吸引子。

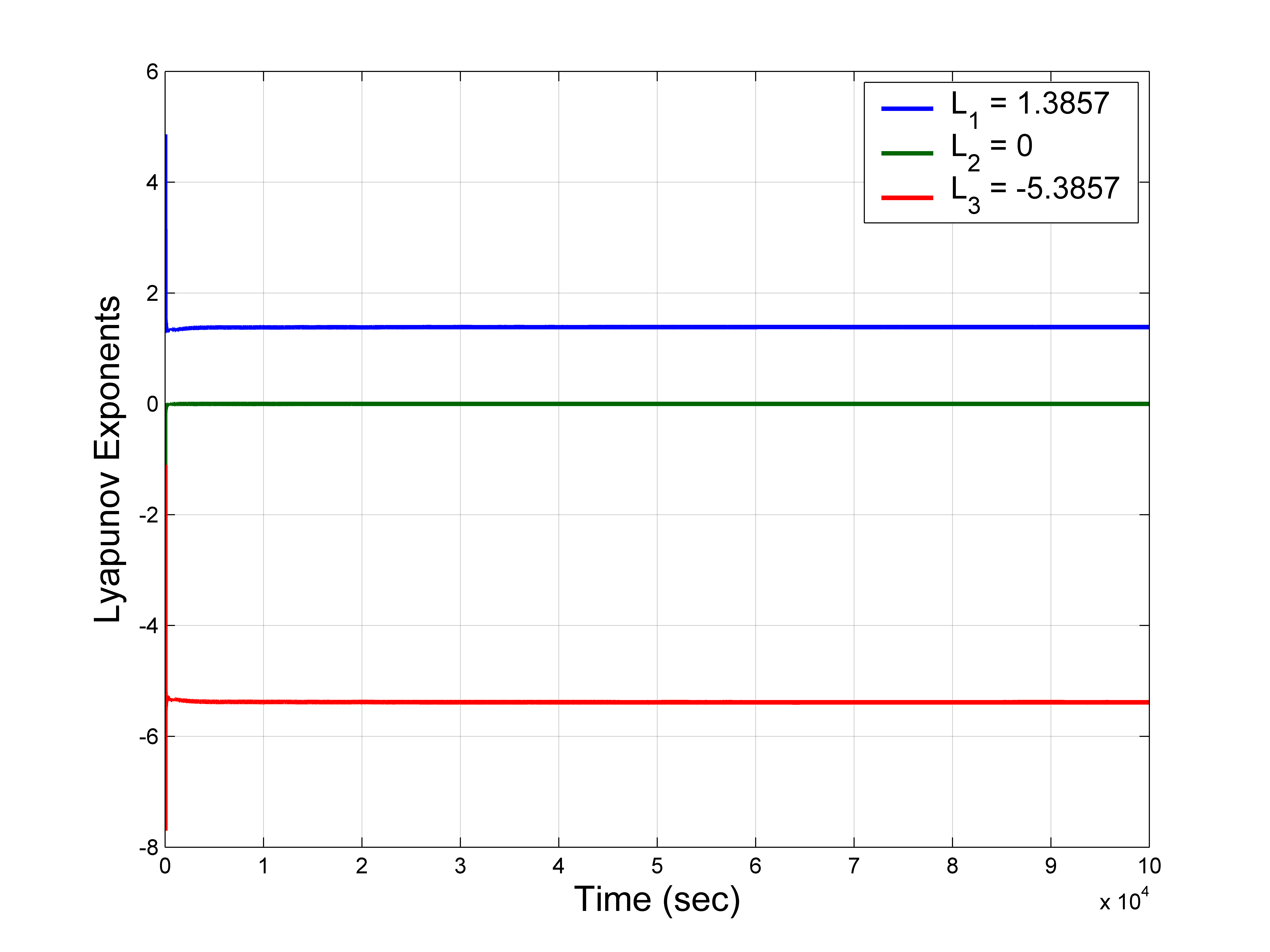
新系统 (1) 在 $(a, b, c) = (3, 1, 1)$ 和 $X(0) = (0.2, 0.2, 0.2)$ 下的李雅普诺夫混沌指数通过沃尔夫算法 (Wolf 等，1985) 确定为 $(L_1, L_2, L_3) = (1.3857, 0, -5.3857)$。

新系统(1)是混沌的，因为 $L_1 > 0$，并且是耗散的，因为 $L_1 + L_2 + L_3 = -4 < 0$。

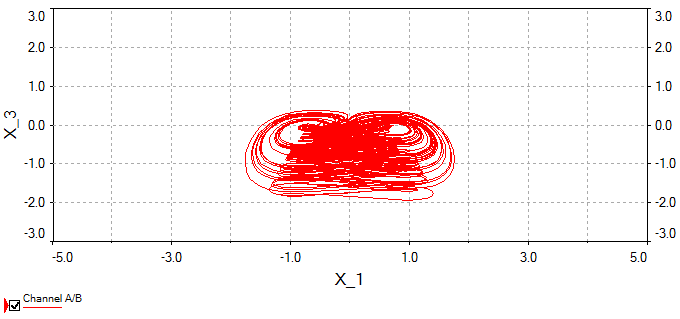
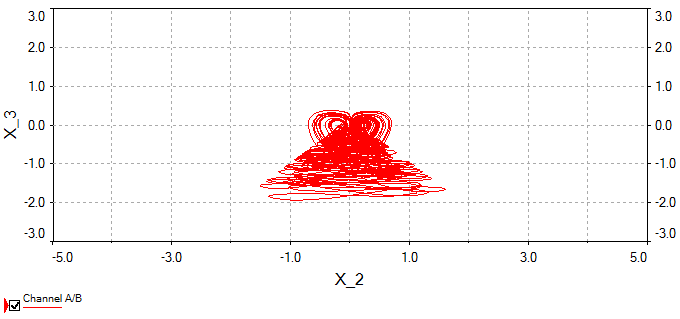
新混沌吸引子 (1) 在 $(a, b, c) = (3, 1, 1)$ 和 $X_0 = (0.2, 0.2, 0.2)$ 下的相图显示在图1–4中。

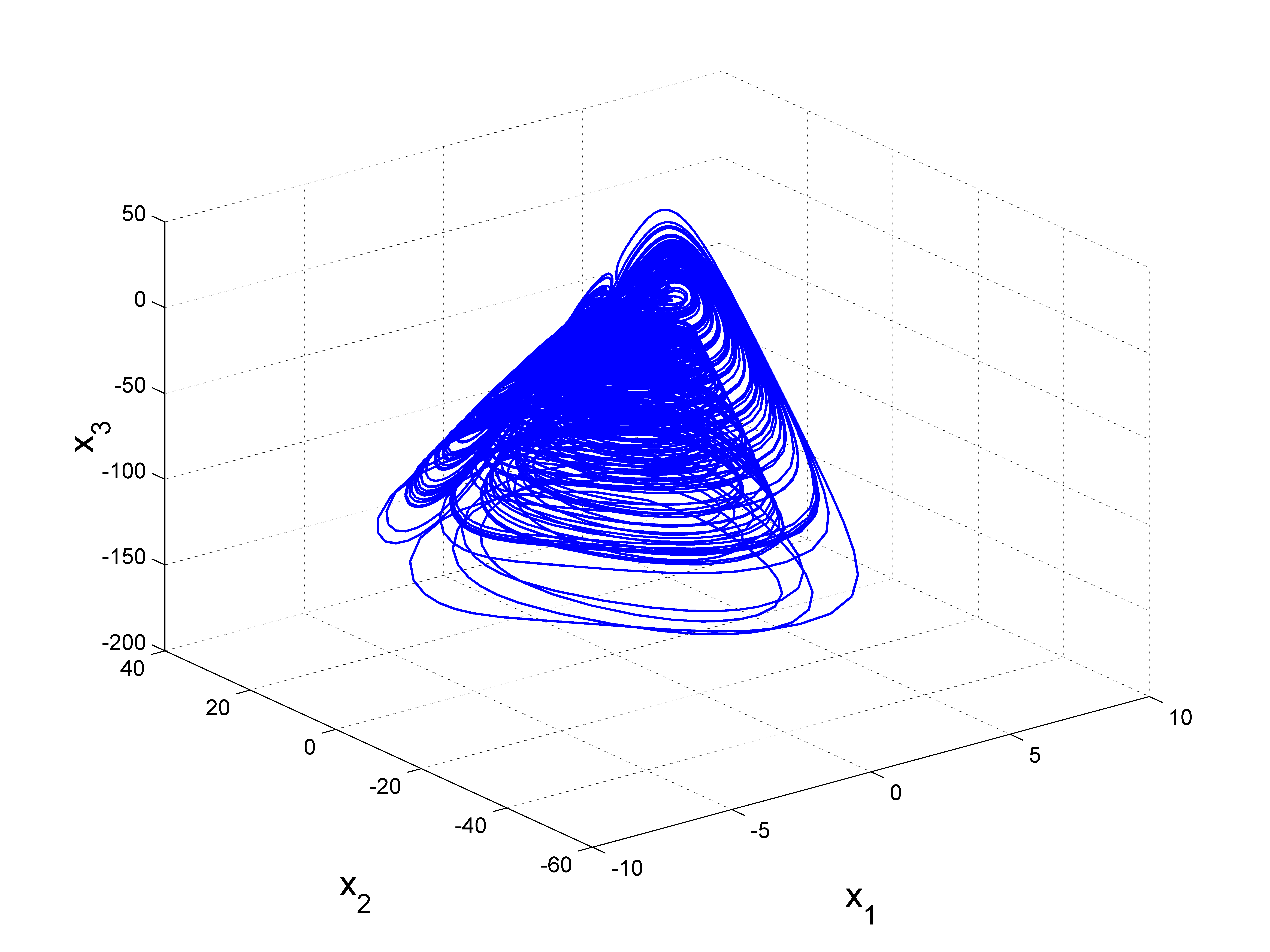
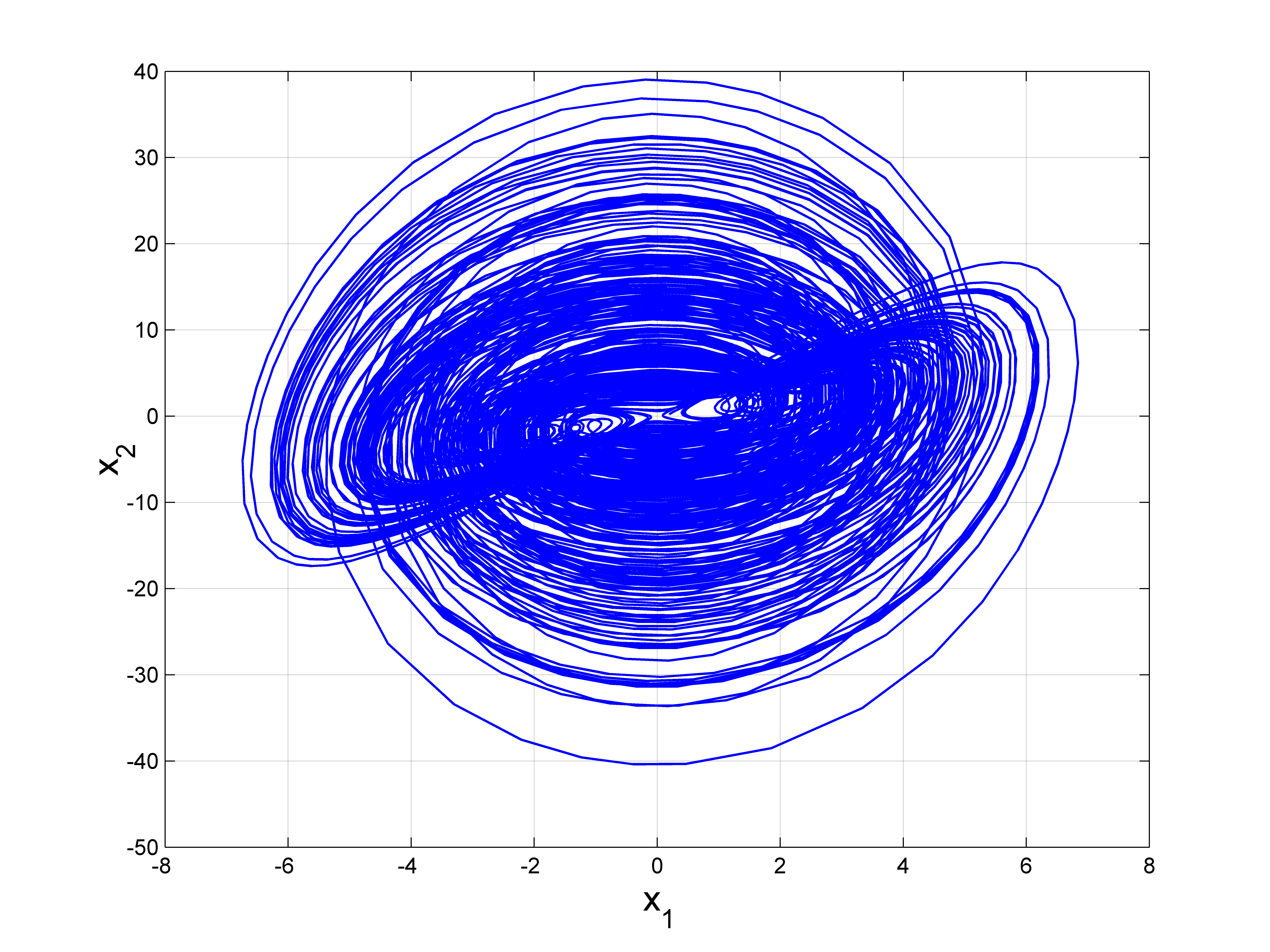
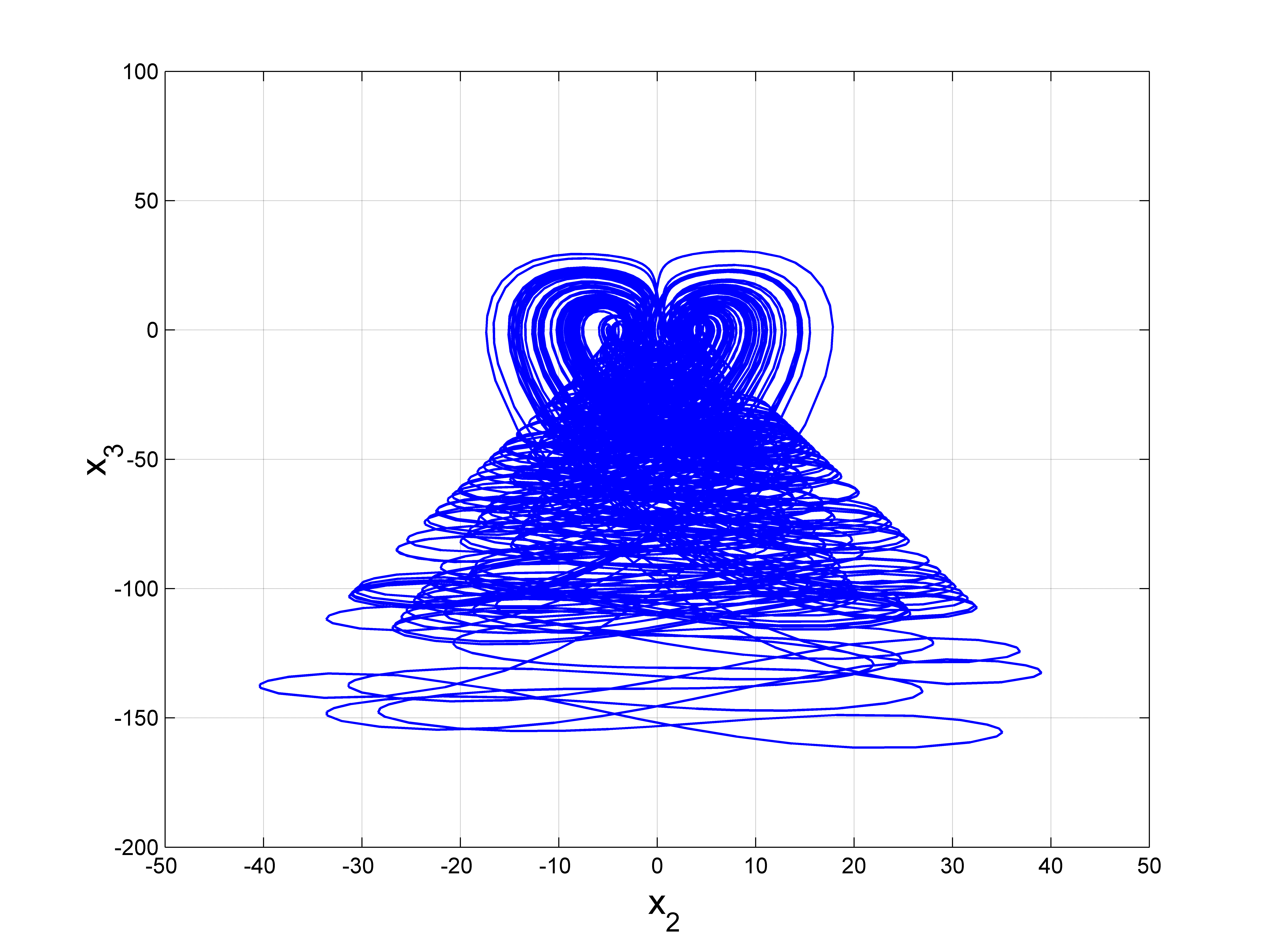
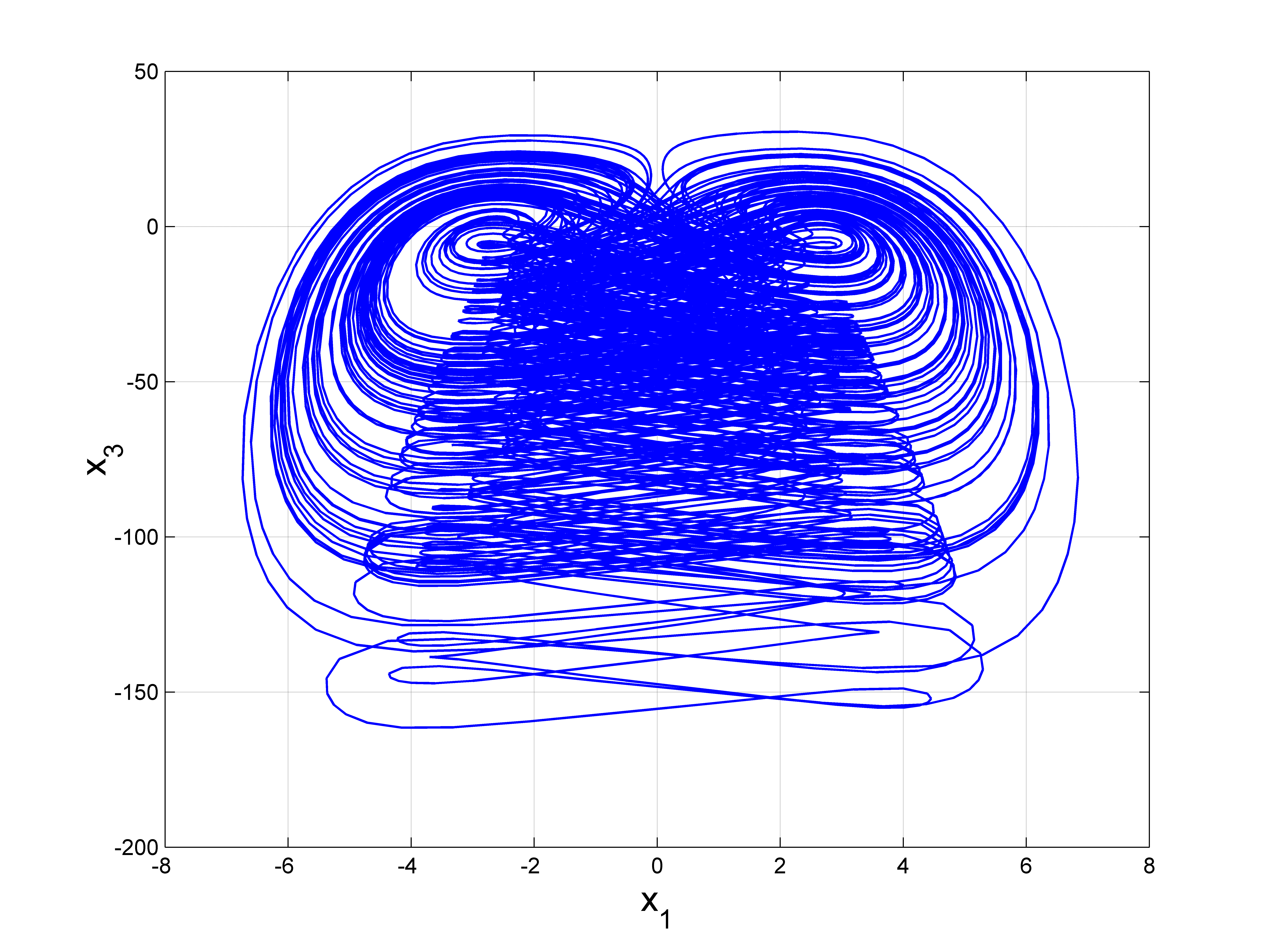
3 新混沌系统的动力学分析

此处，我们假设系统 (1) 的参数处于混沌情况，即 $(a, b, c) = (3, 1, 1)$。

3.1 耗散性

我们将新混沌系统(1)简洁地表示为 $\dot{x} = f(x)$，其中

$$
f(x) = [a(x_2 - x_3) \quad x_1x_3 \quad 50 - bx_1^4 - cx_3]^T \quad (2)
$$

混沌系统(1)的散度如下所示

$$
\nabla \cdot f = \sum_{i=1}^{3} \frac{\partial f_i}{\partial x_i} = -a - c = -4 \quad (3)
$$

对于 $f(X)$ 流的任意体积元 $V(t)$，我们看到

$$
\dot{V}(t) = (\nabla \cdot f)V(t) = -4V(t) \quad (4)
$$

因此，体积元 $V(t)$ 随着 $t \to \infty$ 指数地收缩至零，这表明新的三维系统(1)是耗散的。

3.2 对称性

新混沌系统(1) 关于 $x_3$‐轴具有旋转对称性。这是因为系统方程在坐标变换下保持不变

$$
(x_1, x_2, x_3) \mapsto (-x_1, -x_2, x_3) \quad (5)
$$

由于这种旋转对称性，系统(1)的任何非平凡状态轨迹都有一条对称轨迹。

3.3 平衡点

通过求解以下方程组，可以找到新混沌系统(1)的平衡点（或平衡点）。

$$
a(x_2 - x_1) = 0, \quad x_1x_3 = 0, \quad 50 - bx_1^4 - cx_3 = 0 \quad (6)
$$

我们针对参数值$(a, b, c) = (3, 1, 1)$求解系统(6)。

为了求解平衡点，我们考虑由 (A) $x_1 = 0$ 和 (B) $x_1 \neq 0$ 给出的两种情况。当 $x_1 = 0$ 时，显然有 $x_2 = 0$ 和 $x_3 = 50$。

在这种情况下，我们得到平衡点

$$
E_1 = \begin{bmatrix} 0 \ 0 \ 50 \end{bmatrix} \quad (7)
$$

当 $x_1 \neq 0$ 很明显 $x_3 = 0$, $x_2 = x_1$ 且 $x_1^4 = 50$

在这种情况下，我们得到平衡点

$$
E_2 = \begin{bmatrix} 2.6591 \ 2.6591 \ 0 \end{bmatrix}, \quad E_3 = \begin{bmatrix} -2.6591 \ -2.6591 \ 0 \end{bmatrix} \quad (8)
$$

对于新混沌系统(1)，在任意 $x \in \mathbb{R}^3$ 处的雅可比矩阵计算如下：

$$
J(x) = \begin{bmatrix}
-3 & 3 & 0 \
x_3 & 0 & x_1 \
-4x_1^3 & 0 & -1
\end{bmatrix} \quad (9)
$$

$J_1 = J(E_1)$ 的谱值在 MATLAB 中获得为

$$
\lambda_1 = -1, \quad \lambda_2 = -13.8390, \quad \lambda_3 = 10.8390 \quad (10)
$$

$J_2 = J(E_2)$ 的谱值在 MATLAB 中获得为

$$
\lambda_1 = -9.8631, \quad \lambda_{2,3} = 2.9316 \pm 7.2273i \quad (11)
$$

$J_3 = J(E_3)$ 的谱值在 MATLAB 中获得为

$$
\lambda_1 = -9.8631, \quad \lambda_{2,3} = 2.9316 \pm 7.2273i \quad (12)
$$

因此，我们推断 $E_1$ 是鞍点，而 $E_2$ 和 $E_3$ 是鞍焦点。新混沌系统(1)的所有平衡点都是双曲的且不稳定的。这也表明新混沌系统(1)的奇异混沌吸引子是一个自激吸引子。

3.4 混沌李雅普诺夫指数

对于新混沌系统(1)，使用沃尔夫算法（沃尔夫等人 (1985)）对$(a, b, c) = (3, 1, 1)$ 和 $X(0) = (0.2, 0.2, 0.2)$ 数值求得李雅普诺夫混沌指数为 $L_1 = 1.3857$、$L_2 = 0$ 和 $L_3 = -5.3857$。由于最大李雅普诺夫指数为 $L_1 = 1.3857 > 0$，我们得出结论：系统(1)是混沌的。

此外，新混沌系统(1)的卡普兰‐约克分形维数确定如下。

$$
D_{KY} = 2 + \frac{L_1 + L_2}{|L_3|} = 2.1623 \quad (13)
$$

$D_{KY}$ 给出了系统(1)复杂性的度量。

4 新混沌系统的自适应控制

本节使用自适应控制技术，针对所有初始条件推导出新三维混沌系统的全局稳定化新结果，且系统参数未知。

我们采用带有反馈控制的新三维混沌系统，其表达式为

$$
\begin{cases}
\dot{x}_1 = a(x_2 - x_1) + u_1 \
\dot{x}_2 = x_1x_3 + u_2 \
\dot{x}_3 = 50 - bx_1^4 - cx_3 + u_3
\end{cases}
\quad (14)
$$

在(14)中，$u_1, u_2, u_3$ 是为在系统参数未知时全局稳定化系统(14)的状态 $x_1, x_2, x_3$ 而设计的自适应控制。

作为自适应反馈控制律，我们考虑

$$
\begin{cases}
u_1 = -A(t)(x_2 - x_1) - G_1x_1 \
u_2 = -x_1x_3 - G_2x_2 \
u_3 = -50 + B(t)x_1^4 + C(t)x_3 - G_3x_3
\end{cases}
\quad (15)
$$

在(15)中，$(A(t), B(t), C(t))$ 是未知系统参数 $(a, b, c)$ 的时变估计，且 $G_1, G_2, G_3$ 为正增益常数。

反馈律（15）的实现导致系统

$$
\begin{cases}
\dot{x}_1 = a - A(t) - G_1x_1 \
\dot{x}_2 = -G_2x_2 \
\dot{x}_3 = -[b - B(t)]x_1^4 - [c - C(t)]x_3 - G_3x_3
\end{cases}
\quad (16)
$$

为了简化计算，我们将参数估计误差定义为

$$
e_a = a - A(t), \quad e_b = b - B(t), \quad e_c = c - C(t) \quad (17)
$$

我们可以将参数估计误差(17)简洁地表示为

$$
\xi(t) = [e_a(t) \quad e_b(t) \quad e_c(t)]^T \quad (18)
$$

利用 (17)，闭环动力学 (16) 可以简洁地表示为

$$
\begin{cases}
\dot{x}_1 = e_a(x_2 - x_1) - G_1x_1 \
\dot{x}_2 = -G_2x_2 \
\dot{x}_3 = -e_bx_1^4 - e_cx_3 - G_3x_3
\end{cases}
\quad (19)
$$

对 (17) 关于时间进行微分，我们得到

$$
\dot{e}_a = \dot{A}, \quad \dot{e}_b = \dot{B}, \quad \dot{e}_c = \dot{C} \quad (20)
$$

下一个结果是本节的主要结果，该结果通过使用李雅普诺夫稳定性理论（Vukic 等，2003）建立。

定理1 ：新混沌系统(14)在参数集未知（a, b, c）的情况下，通过自适应控制律(15)以及如下参数更新律，可对所有初始条件实现全局且指数地稳定，其中 $G_1, G_2, G_3$ 为正增益常数。

$$
\begin{cases}
\dot{A} = x_1(x_2 - x_1) \
\dot{B} = -x_1^4x_3 \
\dot{C} = -x_3^2
\end{cases}
\quad (21)
$$

证明 ： 首先，我们考虑由方程定义的李雅普诺夫函数

$$
V(x, \xi) = \frac{1}{2}(x_1^2 + x_2^2 + x_3^2 + e_a^2 + e_b^2 + e_c^2), \quad (22)
$$

容易注意到，$V$ 是关于 $\mathbb{R}^6$ 的一个二次且正定函数。

通过对 $V$ 沿(19)和(20)轨迹进行微分，我们注意到以下结果。

$$
\dot{V} = -G_1x_1^2 - G_2x_2^2 - G_3x_3^2 + e_b[-x_1^4x_3 - \dot{B}] + e_c[-x_3^2 - \dot{C}] \quad (23)
$$

结合(21)和(23)，我们推导出结果

$$
\dot{V} = -G_1x_1^2 - G_2x_2^2 - G_3x_3^2 \quad (24)
$$

显然，$\dot{V}$ 是关于 $\mathbb{R}^6$ 的一个二次且负半定函数。

根据李雅普诺夫稳定性理论（Vukic 等，2003），立即可知 $x(t)$ 和 $\xi(t)$ 是全局有界的。

我们定义 $G = \min{G_1, G_2, G_3}$。

然后由(24)可得

$$
\dot{V} \leq -G|x|^2 \quad (25)
$$

因此，我们得到

$$
G|x|^2 \leq -\dot{V} \quad (26)
$$

对不等式 (26) 从 0 到 $t$ 进行积分得到

$$
G \int_0^t |x(\tau)|^2 d\tau \leq -\int_0^t \dot{V}(\tau)d\tau = V(0) - V(t) \quad (27)
$$

方程 (27) 表明 $x(t) \in L_2$。

利用(16)，我们推导出 $\dot{x}(t) \in L_\infty$。

根据Barbalat引理（Vukic等人(2003)），我们得出结论：对于所有初始条件 $x(0) \in \mathbb{R}^3$，$x(t) \to 0$ 指数地趋近于 $t \to \infty$。

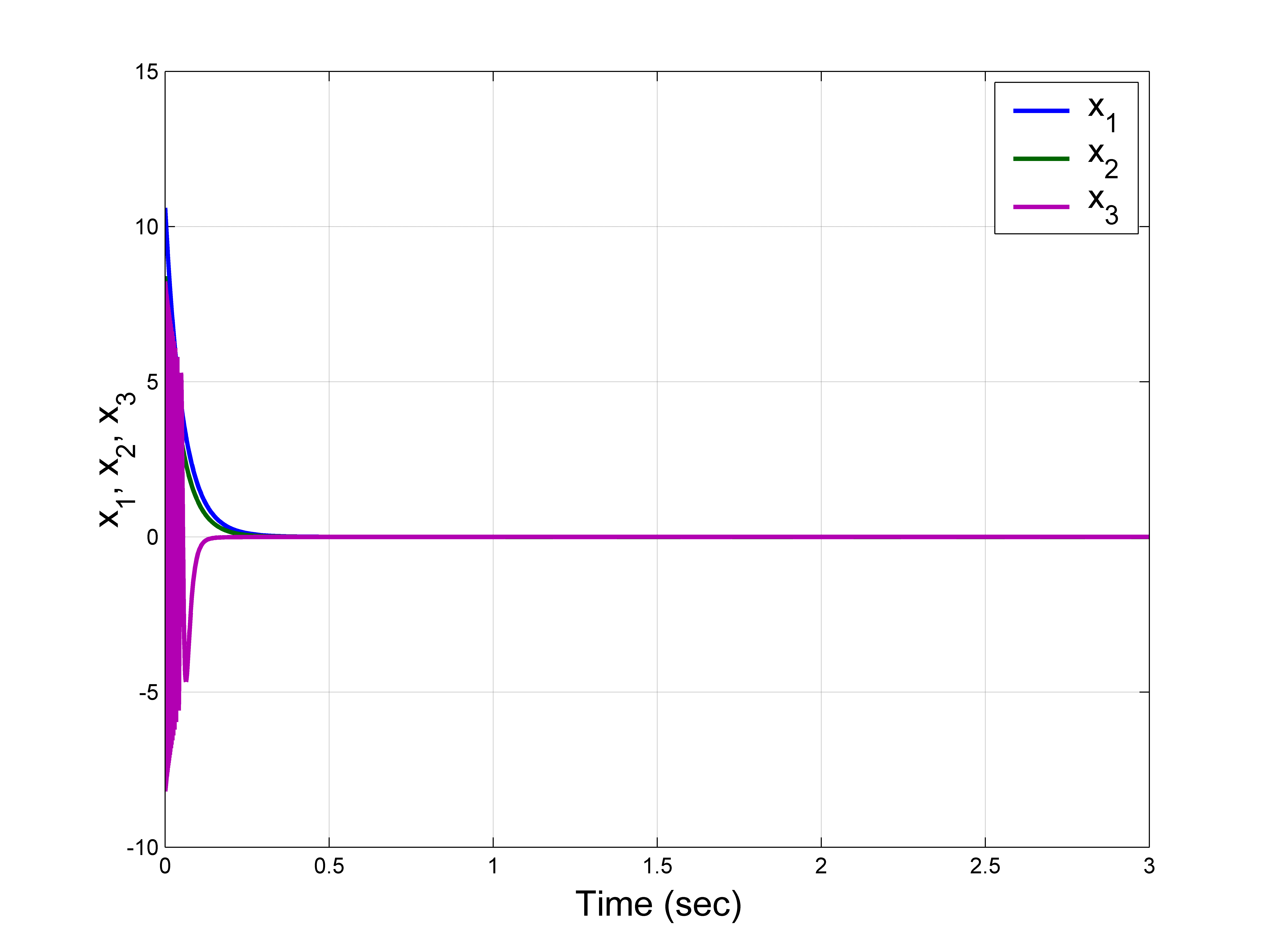
在MATLAB仿真中，我们将参数设为$(a, b, c) = (3, 1, 1)$。作为反馈增益，我们考虑 $G_i = 8$ 用于 $i = 1, 2, 3$。

对于(14)的初始值，我们取 $x(0) = (10.6, 8.4, 5.2)$。参数估计的初始值选为 $A(0) = 9.1$，$B(0) = 7.4$ 和 $C(0) = 6.9$。

5 新混沌系统的自适应同步

本节使用自适应控制技术，针对空间中所有初始条件，推导出一对具有未知参数的新混沌系统作为主系统和从系统实现完全同步的新结果。主要结果通过李雅普诺夫稳定性理论（Vukic 等，2003）建立。

首先，我们将新的三维混沌系统动力学作为主系统，其表达式为

$$
\begin{cases}
\dot{x}_1 = a(x_2 - x_1) \
\dot{x}_2 = x_1x_3 \
\dot{x}_3 = 50 - bx_1^4 - cx_3
\end{cases}
\quad (28)
$$

在(28)式中，$(a, b, c)$ 是未知参数向量。

接下来，我们将带有自适应控制的新的三维混沌系统动力学作为从系统，其表达式为

$$
\begin{cases}
\dot{y}_1 = a(y_2 - y_1) + u_1 \
\dot{y}_2 = y_1y_3 + u_2 \
\dot{y}_3 = 50 - by_1^4 - cy_3 + u_3
\end{cases}
\quad (29)
$$

在(29)中，$u_1, u_2, u_3$ 是待确定的自适应控制，使用时变估计$(A(t), B(t), C(t))$ 来代替未知参数向量$(a, b, c)$。

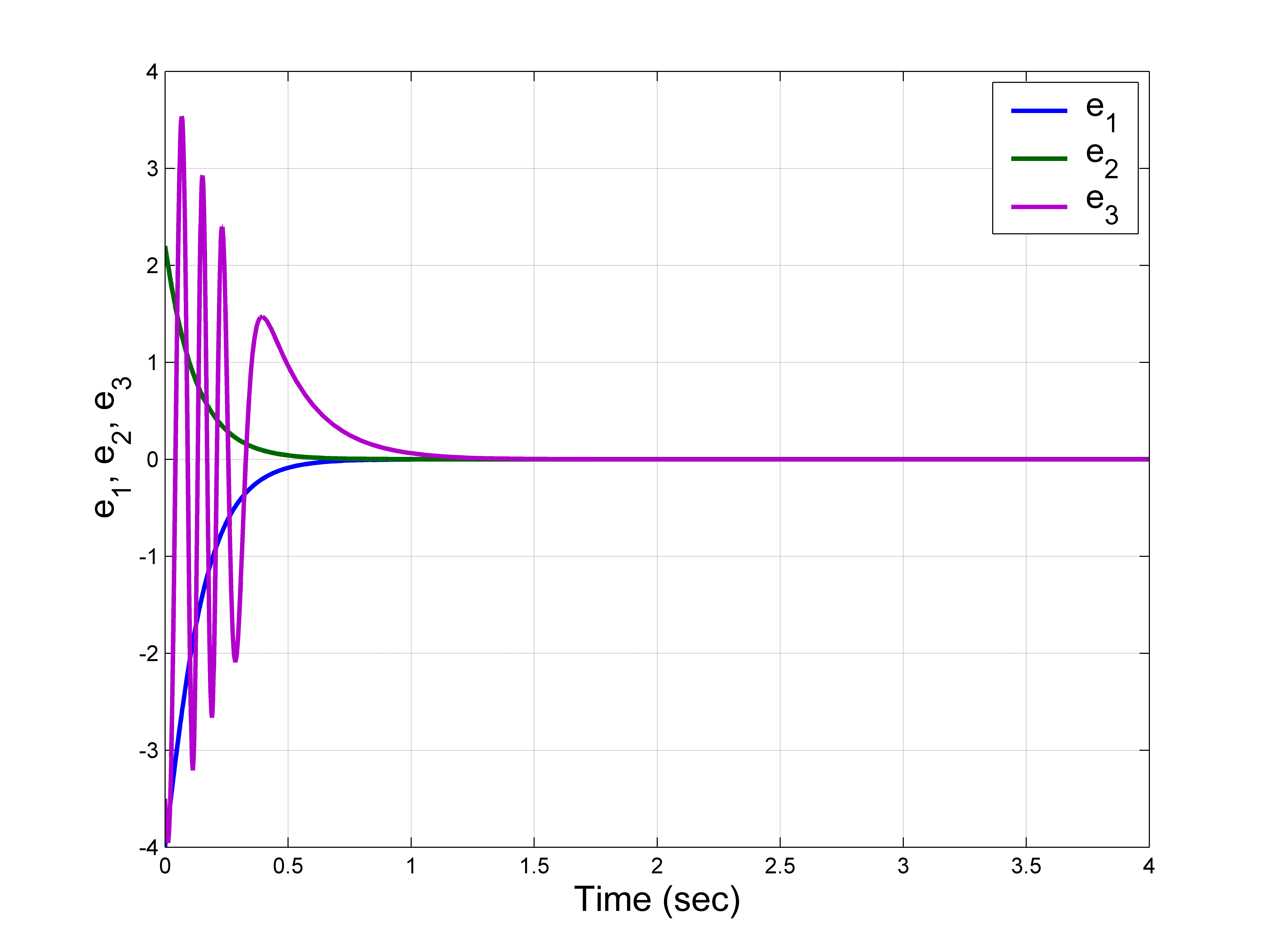
新混沌系统(28)和(29)之间的同步误差由以下方程定义

$$
e_i = y_i - x_i, \quad (i = 1, 2, 3) \quad (30)
$$

我们定义 $e(t) = [e_1(t) \quad e_2(t) \quad e_3(t)]^T$ 为完全同步误差。

很容易推导出如下系统的完全同步误差动态。

$$
\begin{cases}
\dot{e}_1 = a(e_2 - e_1) + u_1 \
\dot{e}_2 = y_1y_3 - x_1x_3 + u_2 \
\dot{e}_3 = -b(y_1^4 - x_1^4) - ce_3 + u_3
\end{cases}
\quad (31)
$$

我们采用由以下方程给出的自适应反馈控制律。

$$
\begin{cases}
u_1 = -A(t)(e_2 - e_1) - G_1e_1 \
u_2 = -y_1y_3 + x_1x_3 - G_2e_2 \
u_3 = B(t)(y_1^4 - x_1^4) + C(t)e_3 - G_3e_3
\end{cases}
\quad (32)
$$

其中 $G_1, G_2, G_3$ 为正增益常数。

结合(31)和(32)，我们得到闭环系统

$$
\begin{cases}
\dot{e}_1 = a - A(t) - G_1e_1 \
\dot{e}_2 = -G_2e_2 \
\dot{e}_3 = - b - B(t) - [c - C(t)]e_3 - G_3e_3
\end{cases}
\quad (33)
$$

为了简化(33)，我们将参数估计误差定义为

$$
e_a = a - A(t), \quad e_b = b - B(t), \quad e_c = c - C(t) \quad (34)
$$

我们还定义 $\xi(t) = [e_a(t) \quad e_b(t) \quad e_c(t)]^T$ 为参数估计误差。

利用(17)，可以轻松将(16)重写为

$$
\begin{cases}
\dot{e}_1 = e_a(e_2 - e_1) - G_1e_1 \
\dot{e}_2 = -G_2e_2 \
\dot{e}_3 = -e_b(y_1^4 - x_1^4) - e_ce_3 - G_3e_3
\end{cases}
\quad (35)
$$

对(34)式关于时间求微分，我们得到

$$
\dot{e}_a = -\dot{A}, \quad \dot{e}_b = -\dot{B}, \quad \dot{e}_c = -\dot{C} \quad (36)
$$

下述结果是本节的主要结果，通过使用李雅普诺夫稳定性理论（Vukic 等，2003）建立。

定理2 ： 新混沌系统(28)和(29)在参数集未知的情况下$(a, b, c)$ 通过自适应控制，对于所有初始条件均实现全局且指数同步

控制律(32)以及以下参数更新律，其中 $G_1, G_2, G_3$ 为正常数。

$$
\begin{cases}
\dot{A} = e_1(e_2 - e_1) \
\dot{B} = -e_3(y_1^4 - x_1^4) \
\dot{C} = -e_3^2
\end{cases}
\quad (37)
$$

证明 ： 首先，我们考虑给定的二次李雅普诺夫函数

$$
V(e, \xi) = \frac{1}{2}(e_1^2 + e_2^2 + e_3^2 + e_a^2 + e_b^2 + e_c^2), \quad (38)
$$

这是一个在 $\mathbb{R}^6$ 上的正定函数。

对 $V$ 沿(35)和(36)的轨迹求导，得到

$$
\dot{V} = -G_1e_1^2 - G_2e_2^2 - G_3e_3^2 + e_b[-(y_1^4 - x_1^4)e_3 - \dot{B}] + e_c[-e_3^2 - \dot{C}] \quad (39)
$$

将(37)代入(39)，我们得到

$$
\dot{V} = -G_1e_1^2 - G_2e_2^2 - G_3e_3^2 \quad (40)
$$

显然，$\dot{V}$ 是 $\mathbb{R}^6$ 上的负半定函数。

因此，可以得出结论： $e(t)$ 和 $\xi(t)$ 是全局有界的。

我们定义 $G = \min{G_1, G_2, G_3}$。

然后由 (40) 可得

$$
\dot{V} \leq -G|e|^2 \quad (41)
$$

or

$$
G|e|^2 \leq -\dot{V} \quad (42)
$$

对不等式(42) 从 0 到 $t$ 积分，我们得到

$$
G \int_0^t |e(\tau)|^2 d\tau \leq -\int_0^t \dot{V}(\tau)d\tau = V(0) - V(t) \quad (43)
$$

由 (43) 可知，$e(t) \in L_2$。

利用 (33)，我们可以得出结论： $\dot{e}(t) \in L_\infty$。

因此，利用Barbalat引理（Vukic等人(2003)），我们可以得出结论：对于所有初始条件 $e(0) \in \mathbb{R}^3$，当 $t \to \infty$ 时，$e(t) \to 0$ 指数地收敛。

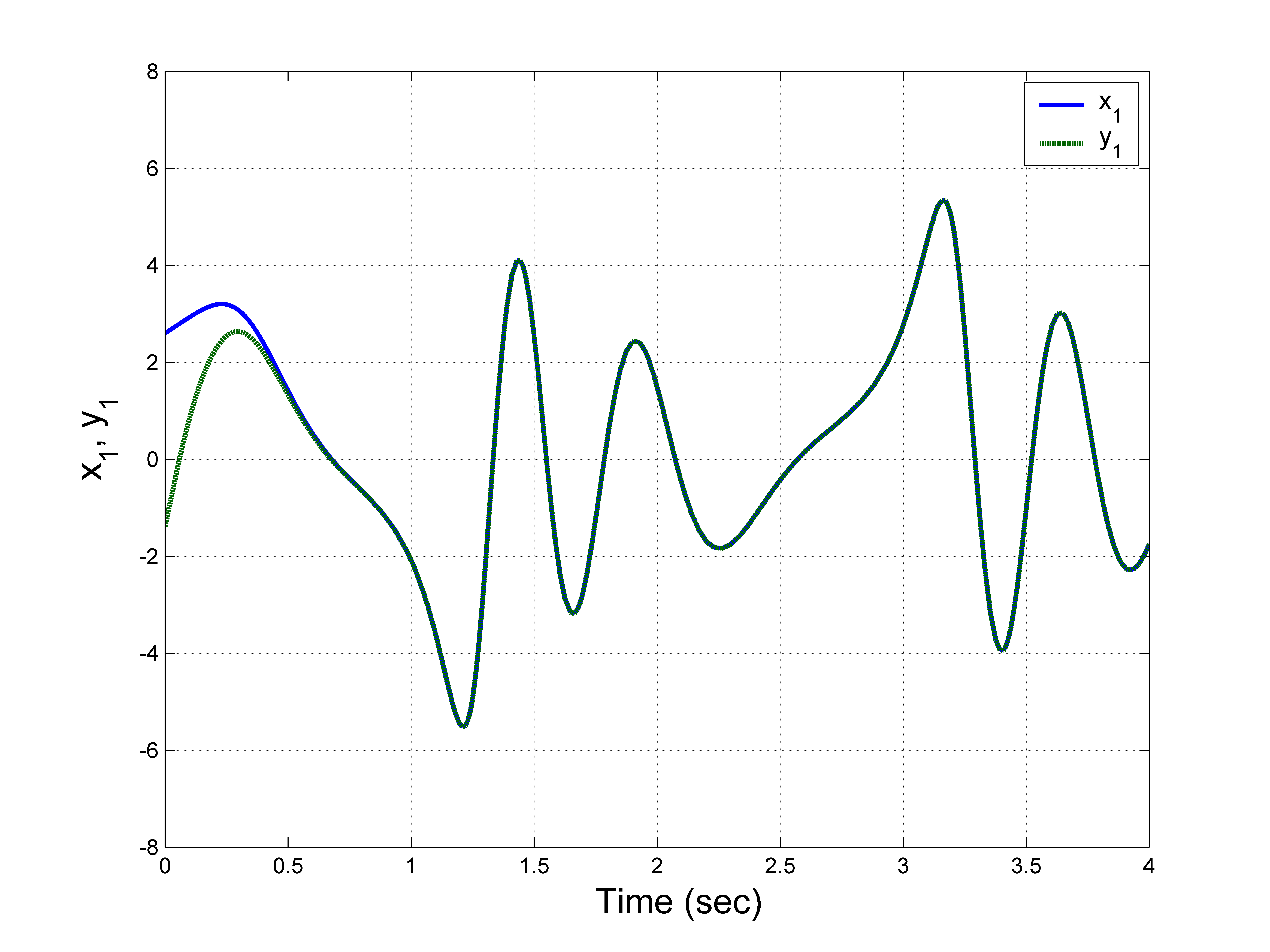
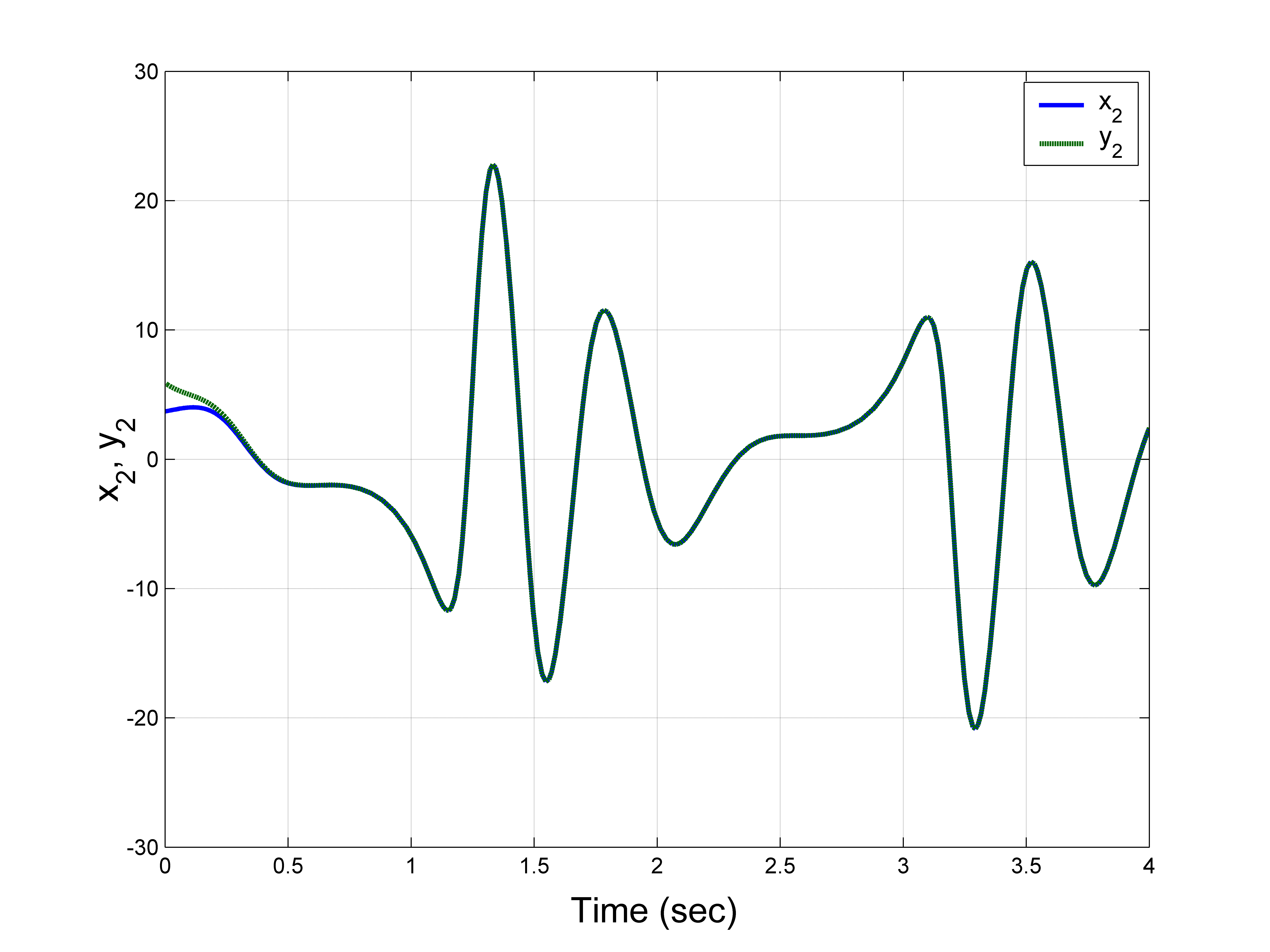
对于MATLAB仿真，我们取新混沌系统的参数值为$(a, b, c) = (3, 1, 1)$。我们取反馈增益为 $G_i = 8$，用于 $i = 1, 2, 3$。

主系统(28)的初始值选择为 $X(0) = (2.6, 3.7, 1.4)$。

从系统（29）的初始值选择为 $Y(0) = (-1.4, 5.9, -2.1)$。

参数估计的初始值选择为 $A(0) = 4.8$，$B(0) = 3.2$ 和 $C(0) = 5.4$。

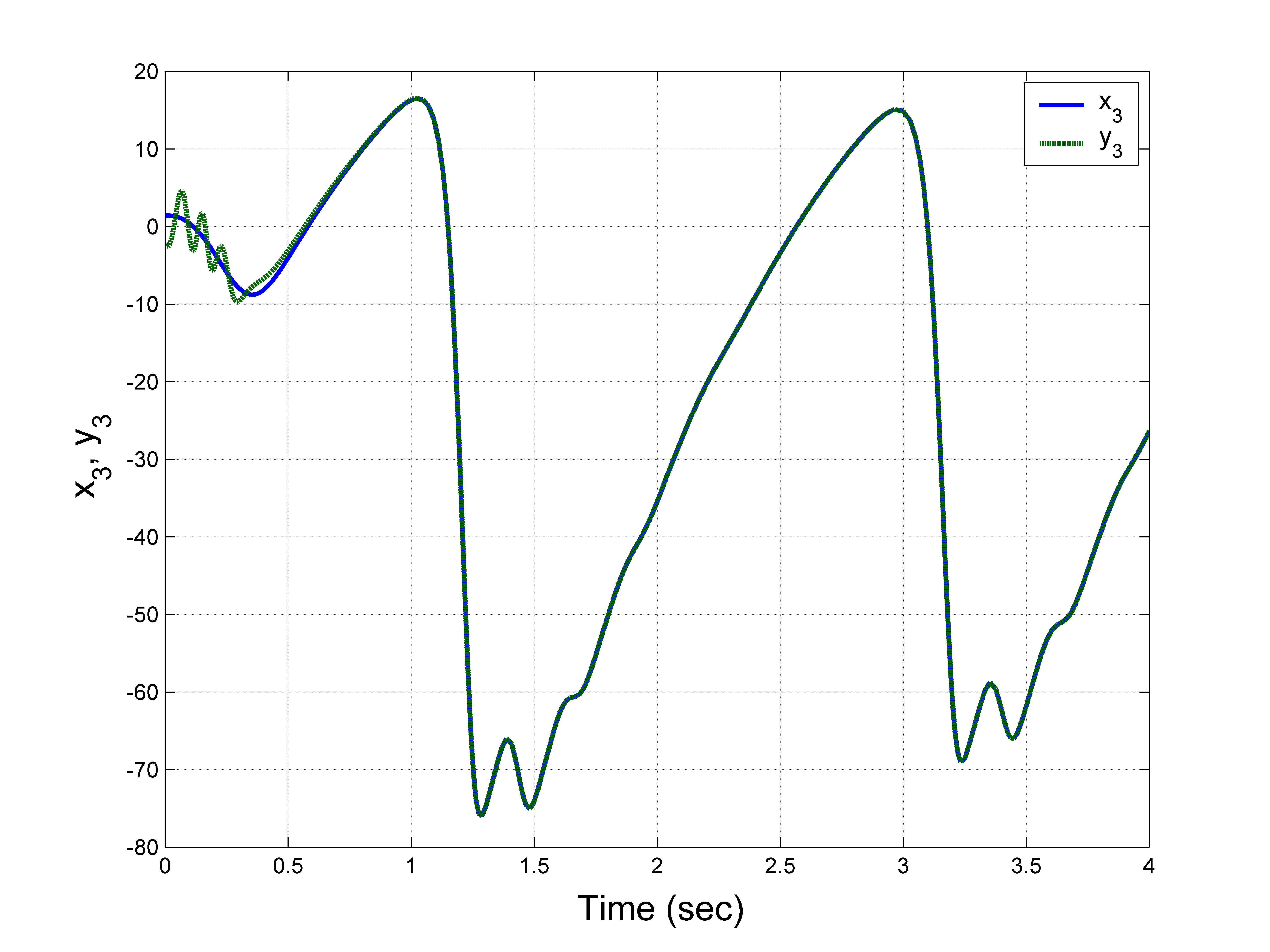
6 新混沌系统的电路实现

为了说明新混沌系统(1)的正确性和可行性，设计了一个用于模拟新系统(1)的电子电路。由于该电子电路是基于运算放大器的方法设计的，因此系统(1)的状态变量被缩小，以在运算放大器的动态范围内获得吸引子。

结果，新混沌系统(1)可以重写为

$$
\begin{cases}
\dot{X}_1 = a \cdot 6.25X_2 - aX_1 \
\dot{X}_2 = 12X_1X_3 \
\dot{X}_3 = 0.67 - b \cdot 3.41X_1^4 - cX_3
\end{cases}
\quad (44)
$$

其中 $X_1 = \frac{x_1}{4}$、$X_2 = \frac{x_2}{25}$ 和 $X_3 = \frac{x_3}{75}$。

所设计电路的原理图如图11所示。

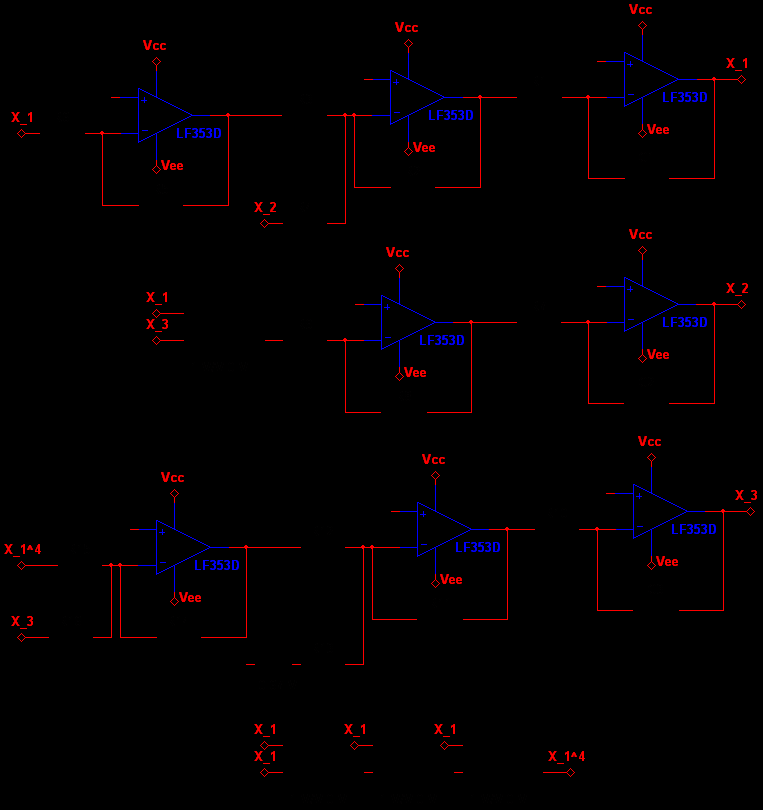
通过对图11中的电子电路应用基尔霍夫定律，得到其电路方程如下形式

$$
\begin{cases}
\frac{dV_{c1}}{dt} = \frac{R_2}{R_1 R_4} V_{c2} - \frac{R_2 R_5}{R_1 R_3 R_6} V_{c1} \
\frac{dV_{c2}}{dt} = \frac{R_8}{R_7 R_9} V_{c1} V_{c3} \
\frac{dV_{c3}}{dt} = \frac{R_{11}}{R_{10} R_{13}} \cdot 0.67 - \frac{R_{11} R_{14}}{R_{10} R_{12} R_{15}} V_{c1}^4 - \frac{R_{11} R_{14}}{R_{10} R_{12} R_{16}} V_{c3}
\end{cases}
\quad (45)
$$

其中 $V_{c1}$、$V_{c2}$ 和 $V_{c3}$ 分别是电容器 $c1$、$c2$ 和 $c3$ 上的电压。系统(44)的状态变量 $X_1$、$X_2$ 和 $X_3$ 分别为电压 $V_{c1}$、$\frac{V_{c2}}{2}$ 和 $\frac{V_{c3}}{75}$。

电路方程(45)变为

$$
\begin{cases}
\dot{X} 1 = \frac{R_2}{R_1 R_4} X_2 - \frac{R_2 R_5}{R_1 R_3 R_6} X_1 \
\dot{X}_2 = \frac{R_8}{R_7 R_9} X_1X_3 \
\dot{X}_3 = \frac{R {11}}{R_{10} R_{13}} \cdot 0.67 - \frac{R_{11} R_{14}}{R_{10} R_{12} R_{15}} X_1^4 - \frac{R_{11} R_{14}}{R_{10} R_{12} R_{16}} X_3
\end{cases}
\quad (46)
$$

我们选用LF353D作为运算放大器，AD633JN作为乘法器来设计电路。输入电源为 $V_{cc} = +15V$ 和 $V_{ee} = -15V$。图11中电子元件的取值选择为与系统(1)的已知参数相匹配。

$$
\begin{aligned}
&R_1 = R_7 = R_{10} = R_{12} = R_{13} = 100k\Omega, \
&R_2 = R_5 = R_6 = R_8 = R_{11} = R_{14} = R_{16} = 10k\Omega, \
&R_3 = 33.33k\Omega, \quad R_4 = 5.33k\Omega, \quad R_9 = 8.33k\Omega, \quad R_{15} = 2.93k\Omega \
&C_1 = C_2 = C_3 = 1nF.
\end{aligned}
$$

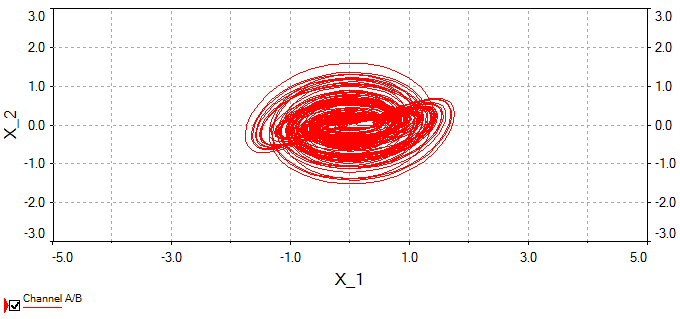
所提出的电路通过使用电子工作台（EWB）实现。

7 结论

在本研究工作中，提出了一种具有两个非线性项的六项新型3D混沌系统，并讨论了其定性性质。结果表明，该新三维混沌系统表现出一个正的李雅普诺夫指数，并具有复杂的动力学行为。此外，通过使用自适应控制器，可以实现具有未知系统参数的相同新三维混沌系统的全局控制和全局混沌同步。为了验证其可行性和理论模型，设计了该新混沌系统的电子电路，相图的电路仿真结果与理论模型高度一致。