潜增长曲线模型(Latent Growth Curve Models, LGCM）

Vol.1前言

在社会科学领域，如心理学、教育学和社会学，甚至是医学领域，研究事物随时间发展的过程是研究者关注的重点。例如，心理学家可能研究自我概念和道德感如何随着年龄的增长而变化；教育学的研究者可能会探讨学生逻辑思维能力如何随着年级的提高而增强；护理学研究可能追踪疾病症状的发展过程。

潜增长曲线模型(Latent Growth Curve Models, LGCM）有助于探究上述问题，该模型可以分析一段时间或某些特定时间点总体的初始状态水平和平均增长趋势，以及个体之间的差异。具体来说，包括：

总体的初始状态水平；

总体的平均增长趋势；

初始状态水平的个体差异；

平均增长趋势的个体差异；

初始状态水平和平均增长趋势的关系；

LGCM有很多种不同的别名。例如，潜在轨迹模型（Latent Trajectory Model，LTM），潜增长曲线模型（LGCM；Kaplan，2000），潜增长模型（Latent Growth Models，LGM）或潜增长曲线模型（Latent Variable Growth Curve Modeling）。如果大家看到不同的叫法，完全不用惊慌，有可能说得是一回事儿。

我们将对该模型的基本原理和mplus应用进行介绍，如果觉得这部分较难理解和枯燥，也可以直接跳到太长不看版(Vol.3)，此处会根据一个例子进行mplus代码撰写和结果讲解。

举例——以线性回归分析为例

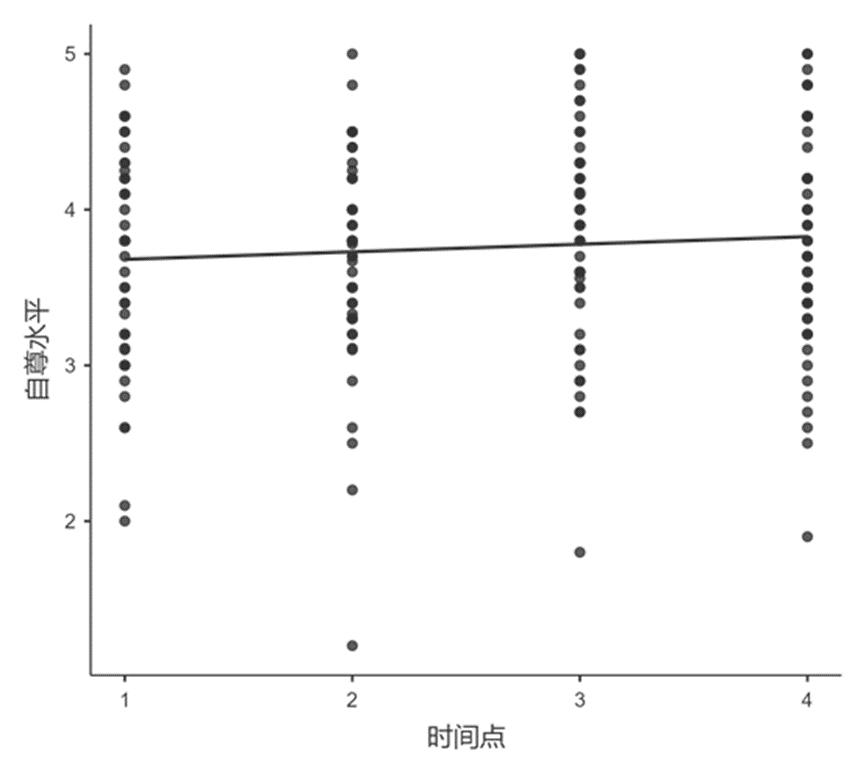
假如我们希望知道初中生自尊水平随时间的变化趋势，为此我们分别于四个时间点测量了50个初中生的自尊水平。

基于线性回归分析的思路，我们可以构建这组被试的回归方程，通过最小二乘法，计算截距b和斜率a。

y = α + βx

·截距α的含义：当自变量为0时，因变量y的值，可以代表初始自尊水平（注：此处并不是第一个时间点的平均自尊水平）。

·斜率β的含义：y随着时间变化时的速率或变化量，它决定了直线的倾斜程度。即每过一个时间点，所有被试自尊水平的平均变化值。

举例——以潜增长曲线模型为例

但基于LGCM的分析思路，我们将同时估计每一个被试回归方程的截距和斜率。

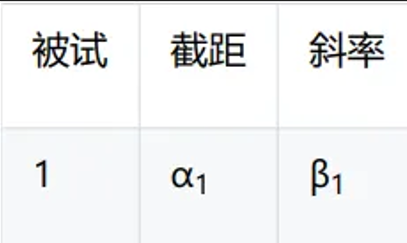
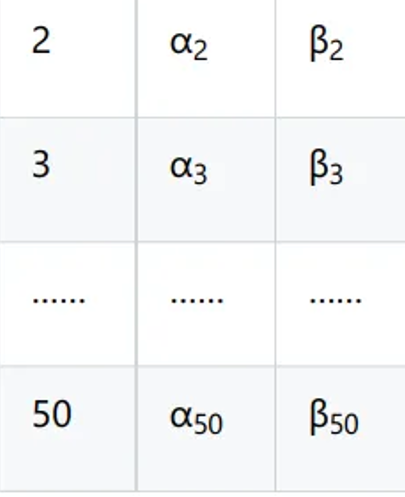
在此基础上，将会进一步估计所有回归方程中所得截距和斜率的均值，代表了变量y的平均初始水平和平均斜率，这部分与线性回归的目标是类似的。

同时，还会进一步估计截距和斜率的方差，代表初始水平和斜率的变异大小。既不同被试在初始自尊水平和自尊水平斜率的差异有多大。

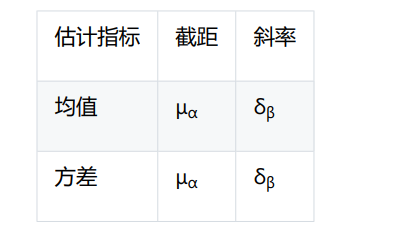
这就意味这，LGCM不仅可以分析个体随时间的发展变化，还可以分析个体间的发展差异，从而为描述变量的发展趋势提供更多的信息。

Vol.2 Mplus应用

主要代码

如果统计基础比较薄弱的小伙伴，基本原理可能听起来不知所云，但在mplus中，只需要在model处加一行简洁的代码，就可以完成LGCM的模型建构和估计。

简洁版代码：

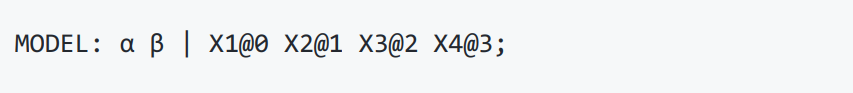
α和β分别代表LGCM的截距和斜率因子，X1-X4代表四个时间点所测量的自尊水平。

当然，你也可以选择下面这个看起来更长更复杂，但是可能更易于进行解读的代码。

加长（fu za）版代码：

当我们结合LGCM的模型图再看这段略显复杂的代码，或许可以更好理解该模型的设定。

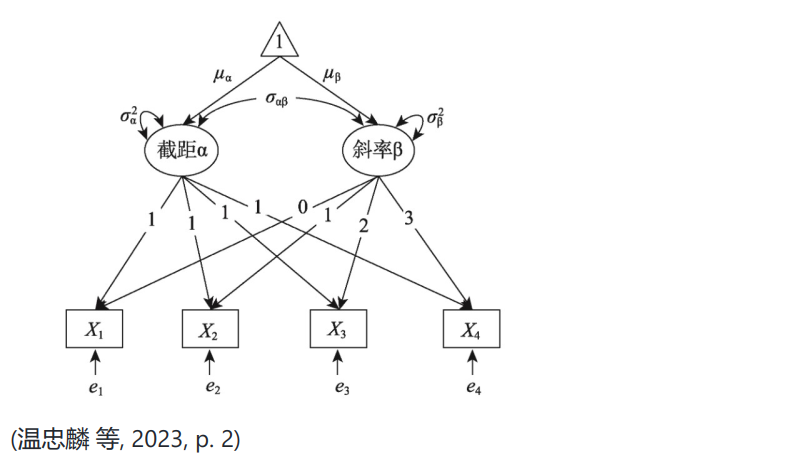
来源：温忠麟, 王一帆, 杜铭诗, 俞雅慧, 张愉蕙, 金童林. (2023). 二阶潜增长模型标度方法及其可比的一阶潜增长模型. 心理学报, 55(8), 1372–1382.

代码解读

模型设定的关键在于：

1.将截距因子α的因素载荷限定为1，即潜变量“截距α”指向X1-X4的四条路经均设定为1，使得潜变量的意义表示初始状态，也就是这行代码：

2.将斜率因子β的因素载荷限定为0、1、2、3，即潜变量“斜率β”指向X1-X4的四条路经分别为0、1、2、3，使得潜变量的意义表示线性变化速度，即这行代码：

3.截距因子α和斜率因子β建立关联，代表初始水平与斜率的关联，即这行代码：

注：该斜率因子β的因素载荷限定代表线性变化，因此是较为常用的线性潜增长曲线模型，此外还有非线性模型，之后有空再介绍。其他几行代码所表示的含义可以通过基础mplus语句得以理解，此处不再做过多解释。

当然，除非你有特殊的模型设定需求，否则还是更建议用简洁版代码，因为更不容易出错。

同时，截距因子通常用i（intercept的首字母），斜率因子通常用s（slop的首字母），这种设定与截距和斜率的英文单词相对应，更容易理解，因此在代码中也更为常见。

Vol.3 太长不看版

假如我们希望知道初中生自尊水平随时间的变化趋势，为此我们分别于四个时间点测量了50个初中生的自尊水平，分别为X1-X4。

3.1 完整代码实例：

i代表截距因子α，s代表斜率因子β。

3.2结果解读：

首先，LGCM作为潜变量模型，大家依旧要先关注模型拟合指标（例如加粗部分），本结果发现RMSEA低于0.08，CFI和TLI大于0.9，似乎还不赖。

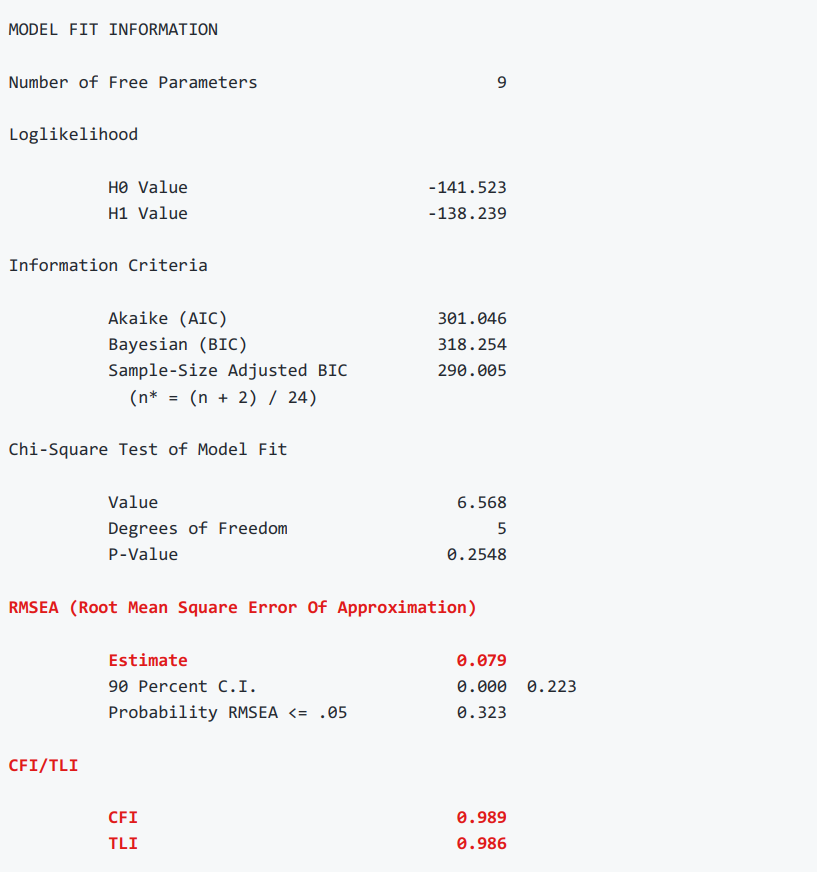
接下来，就是LGCM的主要指标了。当你能对LGCM的基本原理有所理解后，可以直奔最核心的5个指标（加粗部分）。

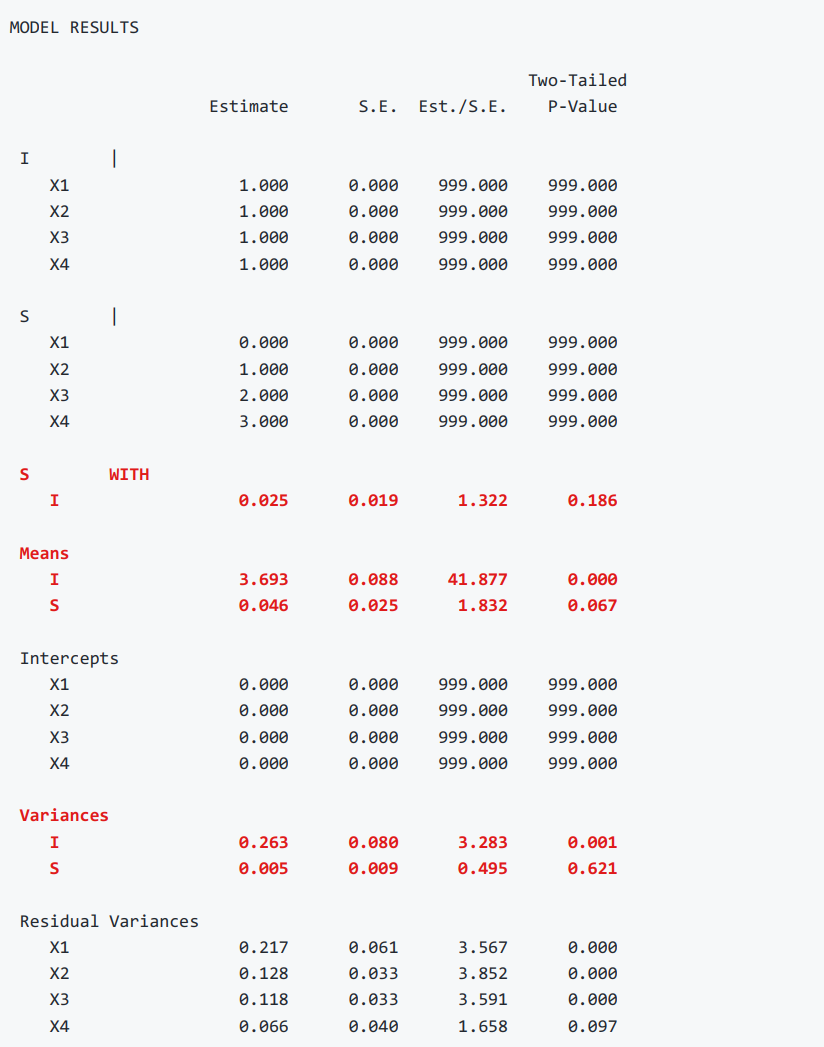
“S  WITH  I “所表示的是截距因子和斜率因子的相关系数，此处为0.025（p = 0.186），提示个体的初始水平与斜率存正相关，即初始自尊水平教高的个体，自尊上升的速度更快，但是没通过显著性检验（p ＞ 0.05）。

Means下I和S分别为截距和斜率的均值估计。值得注意的是，斜率为0.046，比较小，p值也显示为0.067，是不显著的（p ＞ 0.05），说明在这组数据中，随着时间的变化，自尊变化是不显著的，通过回归分析图也可见一斑。

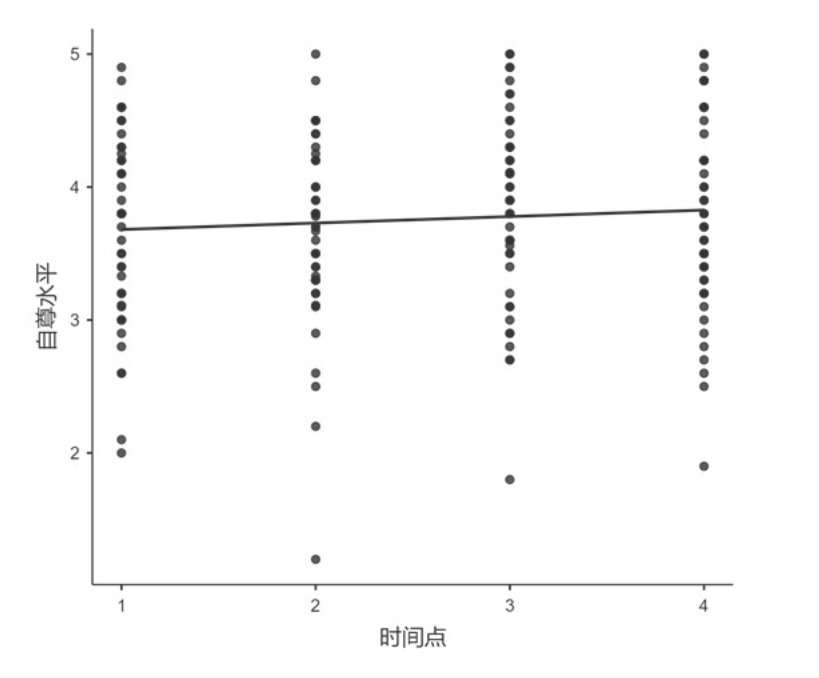
Variances下I和S分别为截距因子和斜率因子的方差估计。截距因子在0.01水平上显著，说明个体在初始自尊水平上存在显著个体间差异。斜率因子在0.05水平上不显著，说明个体在自尊水平变化上不存在显著个体间差异。

下面画了一幅丑图，大家可以尝试理解一下。除了少数被试在自尊水平上会上升或下降，大部分被试在自尊水平变化上比较小，自然个体间差异比较小。但是第一个时间点（近似于初始自尊水平）的差异还是挺大的，从2到5不等。

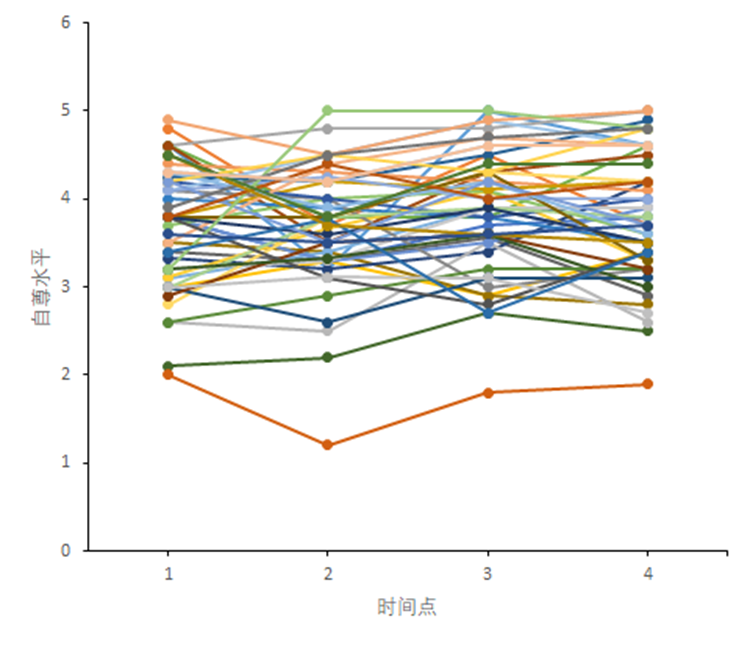
大功告成！

Vol.4 总结

通过与回归分析比较，我们可以发现LGCM不仅可以估计变量的初始水平和变化速率，还可以进一步估计不同个体在初始水平和变化速率上的差异，以及初始水平和变化速率的关系，为群体的发展趋势提供了更细致的描述。

最重要的是，研究者们基于该模型进行了更灵活地拓展，例如探究前因变量对发展轨迹的影响、发展轨迹与和结果变量的关联、不同轨迹之间的关联甚至中介分析、以及探索群体异质性（潜类别增长模型/增长混合模型）。

我们将在之后的推送中与小伙伴分享这些模型。如果这里面有你们心仪的模型，也可以第一时间留言告诉我们，这会激励我们更早地推出哦。

参考文献：

刘红云, 孟庆茂. (2003). 纵向数据分析方法. 心理科学进展, 05, 586–592.

温忠麟, 王一帆, 杜铭诗, 俞雅慧, 张愉蕙, 金童林. (2023). 二阶潜增长模型标度方法及其可比的一阶潜增长模型. 心理学报, 55(8), 1372–1382.

王孟成, 毕向阳. (2018). 潜变量建模与Mplus应用·进阶篇.

PSYCH统计自习室

写在后面

以上就是本期推文的全部内容啦，如果有潜增长曲线模型的其它细节问题，欢迎在评论区留言或者私信，我们很快就会推出相应的内容~