主成分分析(PCA)允许我们总结和可视化包含多个相互关联的定量变量描述的个体/观察的数据集中的信息。每个变量都可以被视为不同的维度。如果你的数据集中有3个以上的变量,那么可视化多维超空间可能会非常困难。
主成分分析用于从多元数据表中提取重要信息,并将这些信息表示为一组称为主成分的新变量。这些新变量对应于原始变量的线性组合。主成分的数量小于或等于原始变量的数量。
给定数据集中的信息对应于它所包含的 total variation 。PCA的目标是识别数据中变化最大的变量(或主成分)。
换句话说,PCA将多变量数据的维度减少到两个或三个主成分,可以以图形方式可视化,信息损失最小。
在本文中,我们描述了PCA的基本思想,并演示了如何使用R软件计算和可视化PCA。此外,我们将展示如何揭示解释数据集中变化的最重要变量。
基础知识
了解PCA的细节需要线性代数的知识。在这里,我们将仅用简单的数据图形表示来解释基础知识。
在下面的图1A中,数据以X-Y坐标系表示。降维是通过识别数据变化的主方向(称为主成分)来实现的。
PCA假设具有最大方差的方向是最“重要”的(即,最主要的)。
在下图中,PC1 坐标轴是样品显示最大变化的第1主成分方向。PC2 坐标轴是第2重要的主成分 ,正交线是PC1的轴。
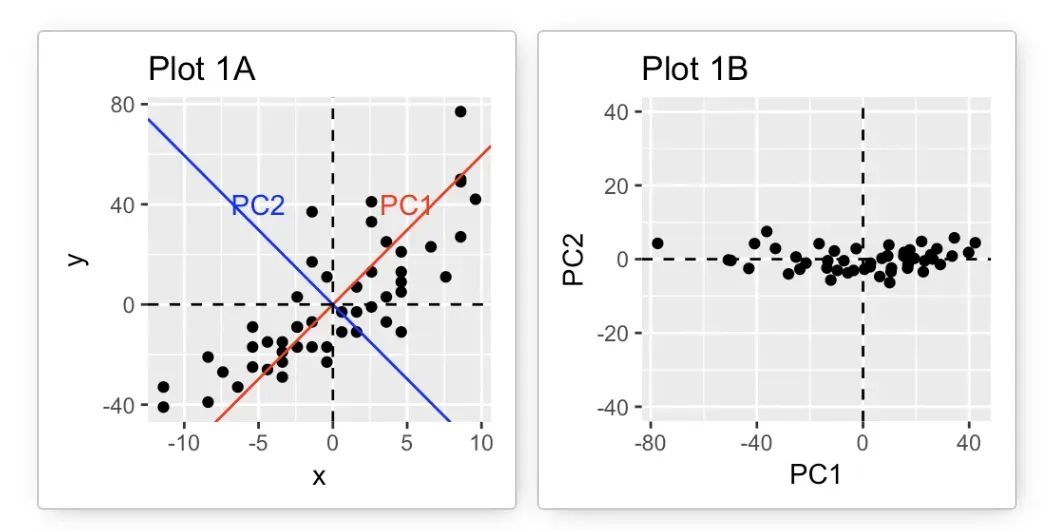
从技术上讲,每个主成分保留的方差量是由所谓的特征值来衡量的。
注意,当数据集中的变量高度相关时,PCA方法特别有用。相关性表明数据中存在冗余。由于这种冗余,PCA可以用于将原始变量减少到更少数量的新变量(=主成分),解释原始变量中的大部分方差。
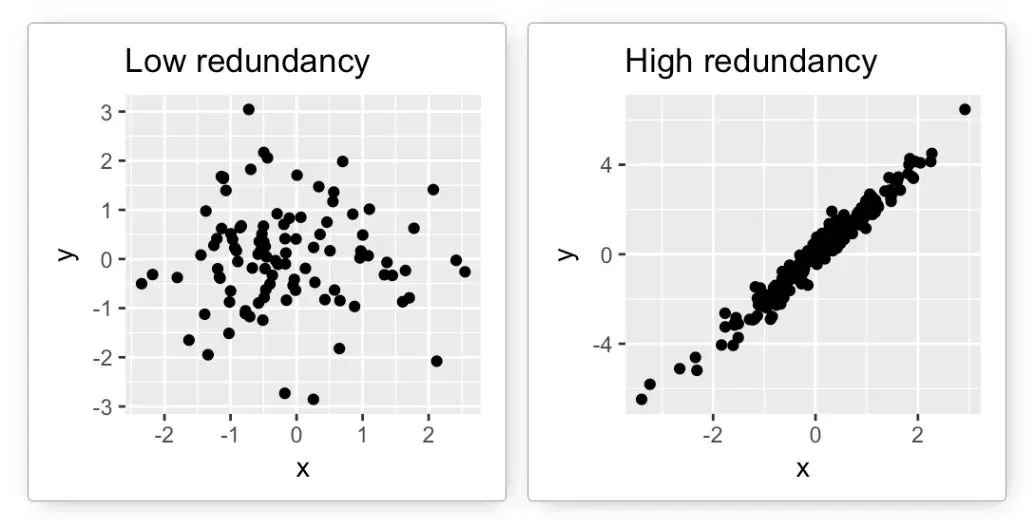
综合起来,主成分分析的主要目的是:
• 识别数据集中隐藏模式
• 通过去除数据中的噪声和冗余来降低数据的维数,
• 识别相关变量
计算
R包
在R软件中有几个来自不同软件包的函数可用于计算PCA:
• prcomp()和princomp()[内置R stats包],
• PCA()[FactoMineR包],
• dudi.pca()[ade4包],
• 和epPCA()[Exposition包]
无论您决定使用什么函数,您都可以使用 factoextra R包中提供的R函数轻松提取和可视化PCA结果。
在本文中,我们将使用两个包FactoMineR(用于分析)和factoextra(用于基于ggplot2的可视化)。
安装两个包如下:
install.packages(c("FactoMineR", "factoextra"))在R中加载它们,通过键入以下内容:
library("FactoMineR")
library("factoextra")数据格式
我们将使用factoextra包中的演示数据集 decathlon2 :
data(decathlon2)
# head(decathlon2)如图3.1所示,这里使用的数据描述了运动员在两个体育赛事(Desctar和OlympicG)中的表现。它包含27个人(运动员)由13个变量描述。
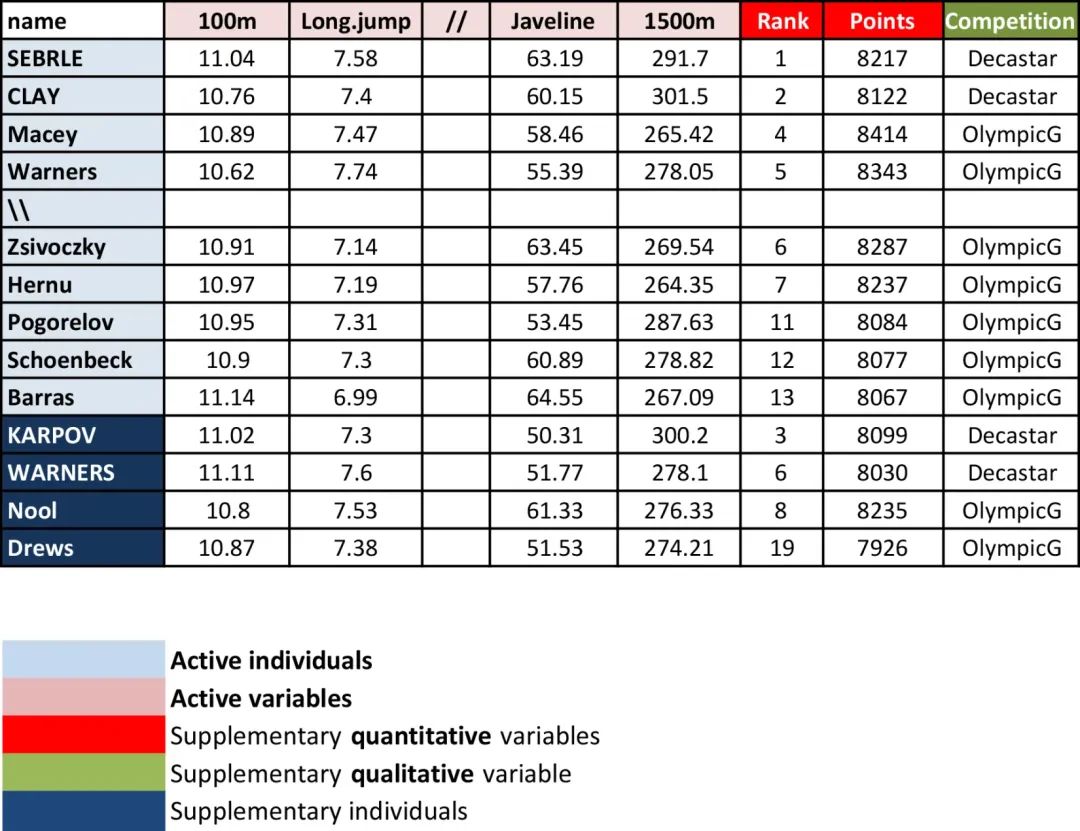
请注意,只有这些个体和变量中的一些将用于执行主成分分析。在PCA之后,将预测因子图上剩余个体和变量的坐标。
在PCA术语中,我们的数据包含:
• 活跃个体(浅蓝色,1:23行):在主成分分析中使用的个体。
• 补充个体(深蓝色,第24:27行):将使用PCA信息和使用活动个体/变量获得的参数预测这些个体的坐标
• 活动变量(粉色,列1:10):用于主成分分析的变量。
• 补充变量:作为补充个体,这些变量的坐标也将被预测。这些可以是:
• 补充连续变量(红色):第11列和第12列分别对应运动员的排名和积分。
• 补充定性变量(绿色):第13列对应于两次运动员会议(2004年奥运会或2004年Decastar)。这是一个分类(或因子)变量因子。它可以用于按组对个体进行着色。
我们首先为主成分分析划分活跃个体和活跃变量的子集:
decathlon2.active <- decathlon2[1:23, 1:10]
head(decathlon2.active[, 1:6], 4)
数据标准化
在主成分分析中,变量通常被标度(即标准化)。当变量以不同的尺度测量时(例如:千克、公里、厘米等),特别建议这样做;否则,所获得的PCA输出将受到严重影响。
目标是使变量具有可比性。一般来说,变量被缩放为i)标准差1和ii)平均值0。
数据标准化是在PCA和聚类分析之前广泛用于基因表达数据分析的方法。当变量的平均值和/或标准差相差很大时,我们也可能想要缩放数据。
当缩放变量时,数据可以转换如下:
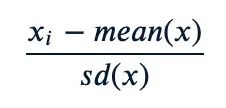
其中 𝑚𝑒𝑎𝑛(𝑥) 是x值的平均值, 𝑠𝑑(𝑥) 是标准差(SD)。
R基函数scale()可用于标准化数据。它以数字矩阵作为输入,并对列执行缩放。
请注意,默认情况下,函数PCA()[in FactoMineR]在PCA期间自动对数据进行转换;因此您不需要在PCA之前进行此转换。
R代码
可以使用函数PCA()[FactoMineR package]。一个简化的格式是:
PCA(X, scale.unit = TRUE, ncp = 5, graph = TRUE)• X :数据框。行是个体,列是数值变量
• scale.unit :逻辑值。如果为TRUE,则在分析前将数据缩放为单位方差。这种标准化到相同的尺度避免了一些变量仅仅因为它们的大测量单位而成为主导变量。它使变量具有可比性。
• ncp :保留在最终结果中的维数。
• graph :逻辑值。如果为TRUE,则显示图形。
下面的R代码,计算活跃个体/变量的主成分分析:
res.pca <- PCA(decathlon2.active, graph = FALSE)函数PCA()的输出是一个列表,包括以下组件:
print(res.pca)
• 使用函数PCA()创建的对象包含许多不同列表和矩阵中的信息。这些值将在下一节中介绍。
可视化和解释
我们将使用factoextra R包来帮助解释PCA。无论您决定使用什么函数[stats::prcomp(),FactoMiner::PCA(),ade 4::dudi.pca(),ExPosition::epPCA()],您都可以使用factoextra R包中提供的R函数轻松提取和可视化PCA结果。
这些功能包括:
• get_eigenvalue(res.pca) :提取主成分的特征值/方差
• fviz_eig(res.pca) :可视化特征值
• get_pca_ind(res.pca) 、 get_pca_var(res.pca) :分别提取个体和变量的结果。
• fviz_pca_ind(res.pca) 、 fviz_pca_var(res.pca) :分别可视化个体和变量的结果。
• fviz_pca_biplot(res.pca) :制作个体和变量的双标图。
在下一节中,我们将演示这些函数。
特征值/方差
如前所述,特征值测量每个主成分保留的变化量。特征值对于第一个PC是大的,对于随后的PC是小的。也就是说,第一PC对应于数据集中具有最大变化量的方向。
我们检查特征值,以确定要考虑的主成分的数量。特征值和方差的比例(即,可以使用函数get_eigenvalue()[factoextra package]提取主成分(PC)保留的信息。
library("factoextra")
eig.val <- get_eigenvalue(res.pca)
eig.val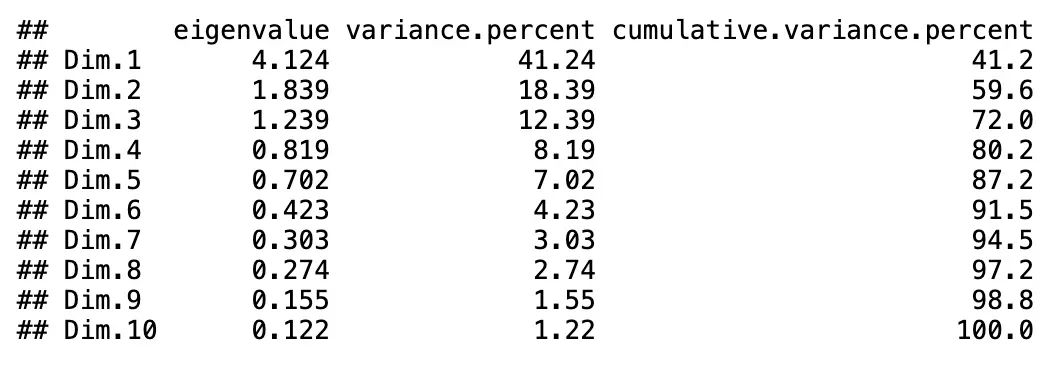
• 所有特征值之和的总方差为10。
第二列给出了每个特征值所解释的变化比例。例如,4.124除以10等于0.4124,或者说,大约41.24%的变化是由这个第一特征值解释的。解释的累积百分比是通过将解释的连续变异比例相加以获得累计总数来获得的。例如,41.242%加上18.385%等于59.627%,等等。因此,约59.627%的变化是由前两个特征值一起解释的。
特征值可用于确定PCA后保留的主成分数量(Kaiser 1961):
• 特征值> 1表示PC比标准化数据中的原始变量之一解释了更多的方差。这通常用作保留PC的截止点。只有当数据标准化时,这才是正确的。
• 您还可以将分量的数量限制为占总方差的某一部分的数量。例如,如果您对解释的总方差的70%感到满意,则使用组件的数量来实现这一点。
不幸的是,没有公认的客观方法来决定多少主成分是足够的。这将取决于具体的应用领域和具体的数据集。在实践中,我们倾向于查看前几个主成分,以便在数据中找到有趣的模式。
在我们的分析中,前三个主成分解释了72%的变异。这是一个可以接受的大百分比。
确定主成分数量的另一种方法是查看Scree Plot,这是从最大到最小排序的特征值图。分量的数目在该点处确定,超过该点,剩余的特征值都相对较小且大小相当(Jollife 2002,Peres-Neto,杰克逊,and索默斯(2005))。
可以使用函数 fviz_eig() 或 fviz_screeplot() [factoextra package]生成碎石图。
fviz_eig(res.pca, addlabels = TRUE, ylim = c(0, 50))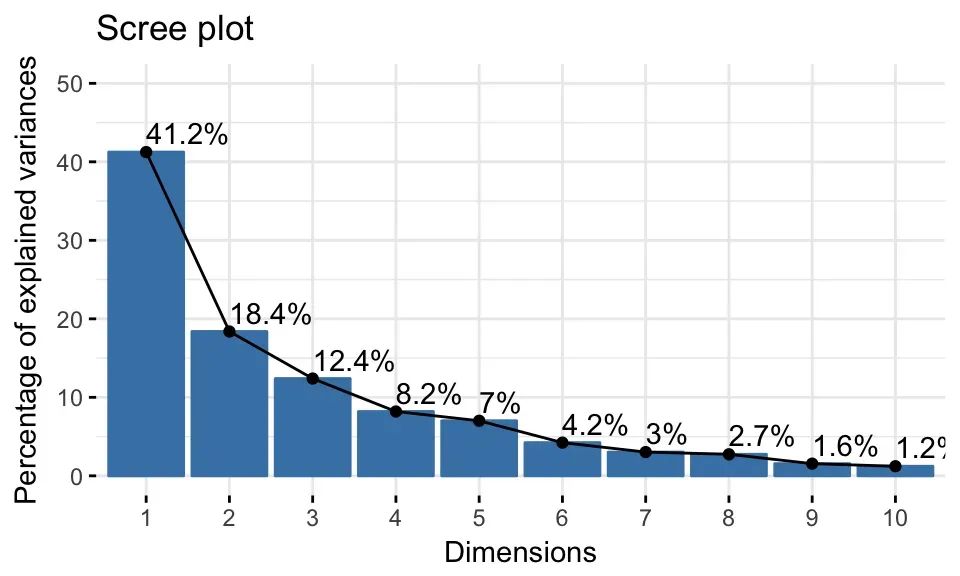
• 从上面的图中,我们可能想停在第五个主成分上。前五个主成分保留了数据中87%的信息(方差)。
变量图
结果
从PCA输出中提取变量结果的一个简单方法是使用函数 get_pca_var() [factoextra package]。此函数提供一个矩阵列表,其中包含活动变量的所有结果(坐标、变量与轴之间的相关性、平方余弦和贡献)
var <- get_pca_var(res.pca)
varget_pca_var() 的组件可用于变量图中,如下所示:
• var$coord :用于创建散点图的变量坐标
• var$cos2 :表示因子图上变量的表示质量。它的计算公式是:var.cos2 = var.coord * var. coord。
• var$contrib :包含变量对主成分的贡献(百分比)。变量(var)对给定主成分的贡献(百分比)为:(var.cos2 * 100)/(成分的总cos 2)。
在本节中,我们将描述如何可视化变量并得出有关其相关性的结论。接下来,我们根据i)它们在因子图上的表示质量或ii)它们对主成分的贡献来突出变量。
相关圆
变量与主成分(PC)之间的相关性用作PC上变量的坐标。变量的表示与观测结果的图不同:观测结果由它们的投影表示,但变量由它们的相关性表示(Abdi和威廉姆斯,2010)。
# Coordinates of variables
head(var$coord, 4)
要绘制变量,请键入以下内容:
fviz_pca_var(res.pca, col.var = "black")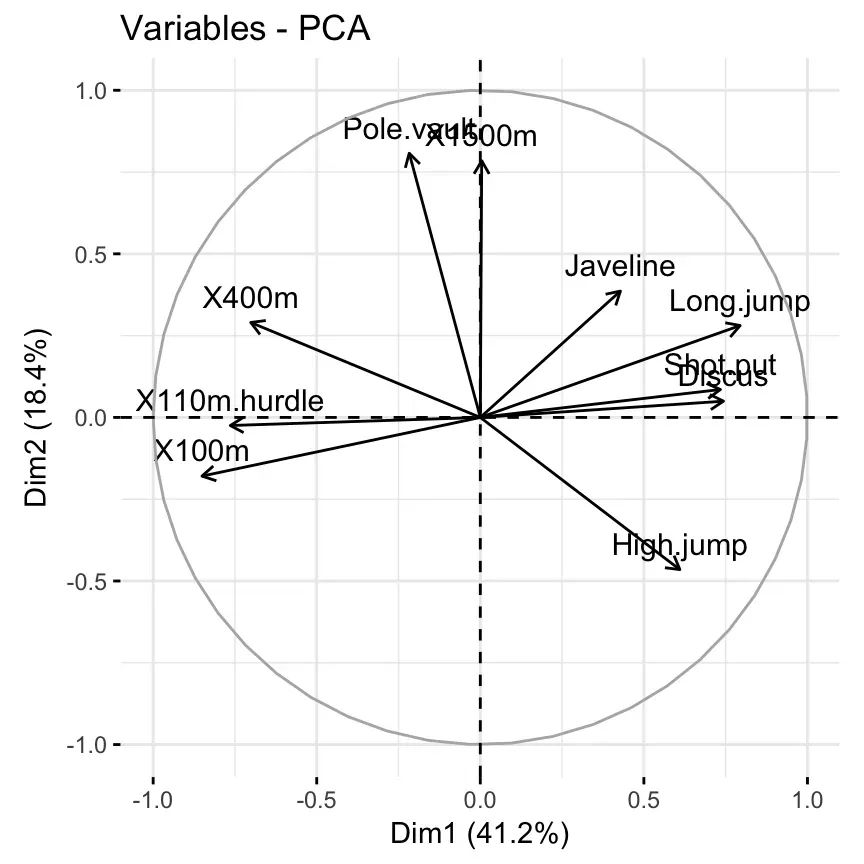
上面的图也称为变量相关图。它显示了所有变量之间的关系。可以解释如下:
• 正相关的变量被分组在一起。
• 负相关变量位于图原点的相对两侧(相对象限)。
• 变量与原点之间的距离衡量因子图上变量的质量。远离原点的变量在因子图上得到了很好的表示。
代表的质量
变量在因子图上的表示质量称为cos2(平方余弦,平方坐标)。您可以按以下方式访问cos2:
head(var$cos2, 4)
您可以使用corrplot软件包可视化所有维度上变量的cos2:
library("corrplot")
corrplot(var$cos2, is.corr=FALSE)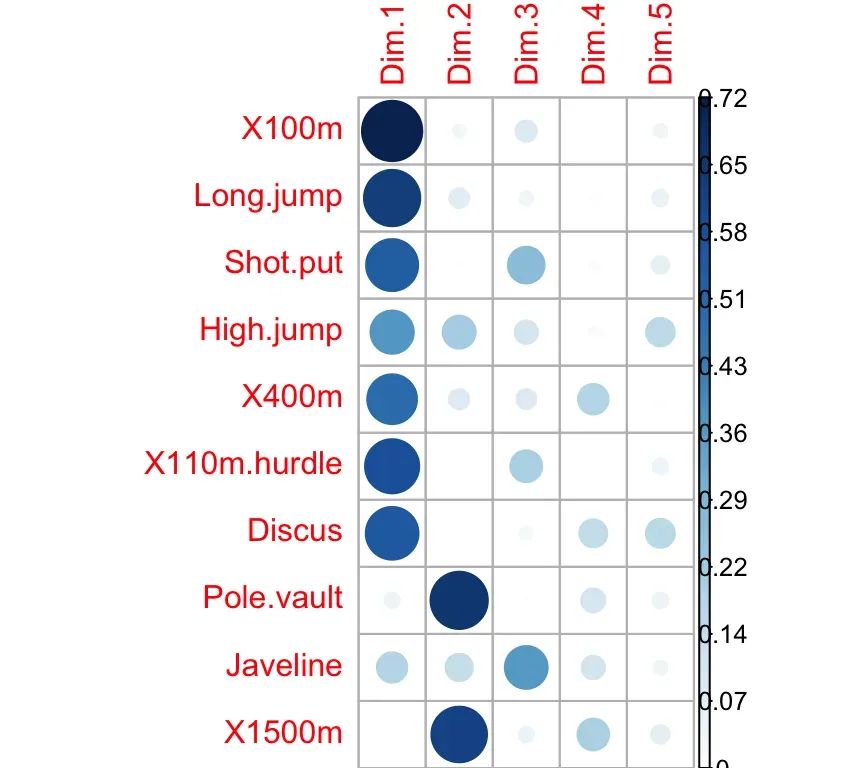
也可以使用函数 fviz_cos2() [in factoextra]创建变量cos2的条形图:
fviz_cos2(res.pca, choice = "var", axes = 1:2)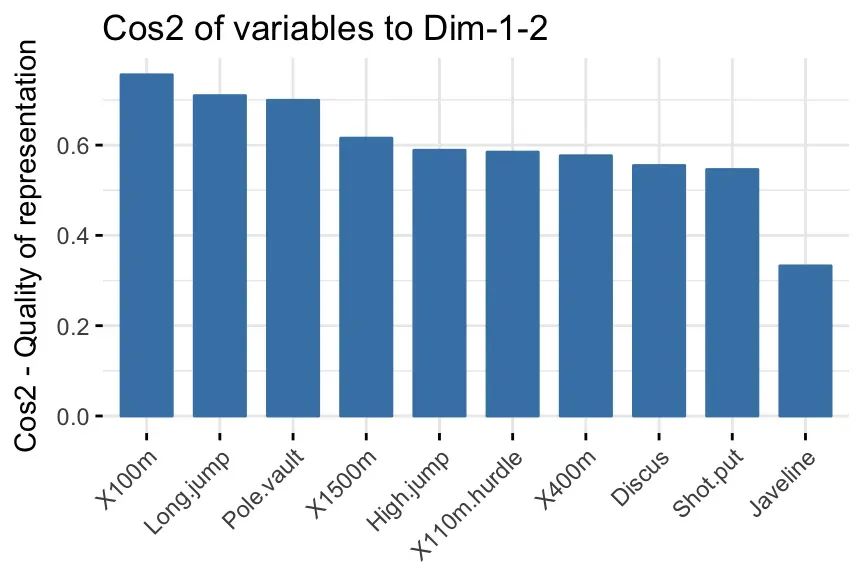
• 高cos2表示变量在主成分上的良好表示。在这种情况下,变量被定位为靠近相关圆的圆周。
• 低cos2表示变量未完全由PC表示。在这种情况下,变量接近圆心。
对于一个给定的变量,所有主成分的cos2之和等于1。
如果一个变量仅由两个主成分(Dim.1和Dim.2)完美表示,则这两个PC上的cos2之和等于1。在这种情况下,变量将位于相关性圆上。
对于某些变量,可能需要2个以上的分量才能完美地表示数据。在这种情况下,变量位于相关性圆内。
总的来说:
• cos2值用于估计表示的质量
• 一个变量越接近相关圆,它在因子图上的表现就越好(解释这些成分也就越重要)
• 靠近图中心的变量对于第一个分量不太重要。
可以使用参数 col.var = "cos2" 根据变量的cos2值为变量着色。这就产生了渐变色。在这种情况下,参数 gradient.cols 可用于提供自定义颜色。例如, gradient.cols = c("white", "blue", "red") 意味着:
• 具有低cos2值的变量将被着色为“白色”
• 具有中间cos2值的变量将被着色为“蓝色”
• 具有高cos2值的变量将被着色为红色
# Color by cos2 values: quality on the factor map
fviz_pca_var(res.pca, col.var = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE # Avoid text overlapping
)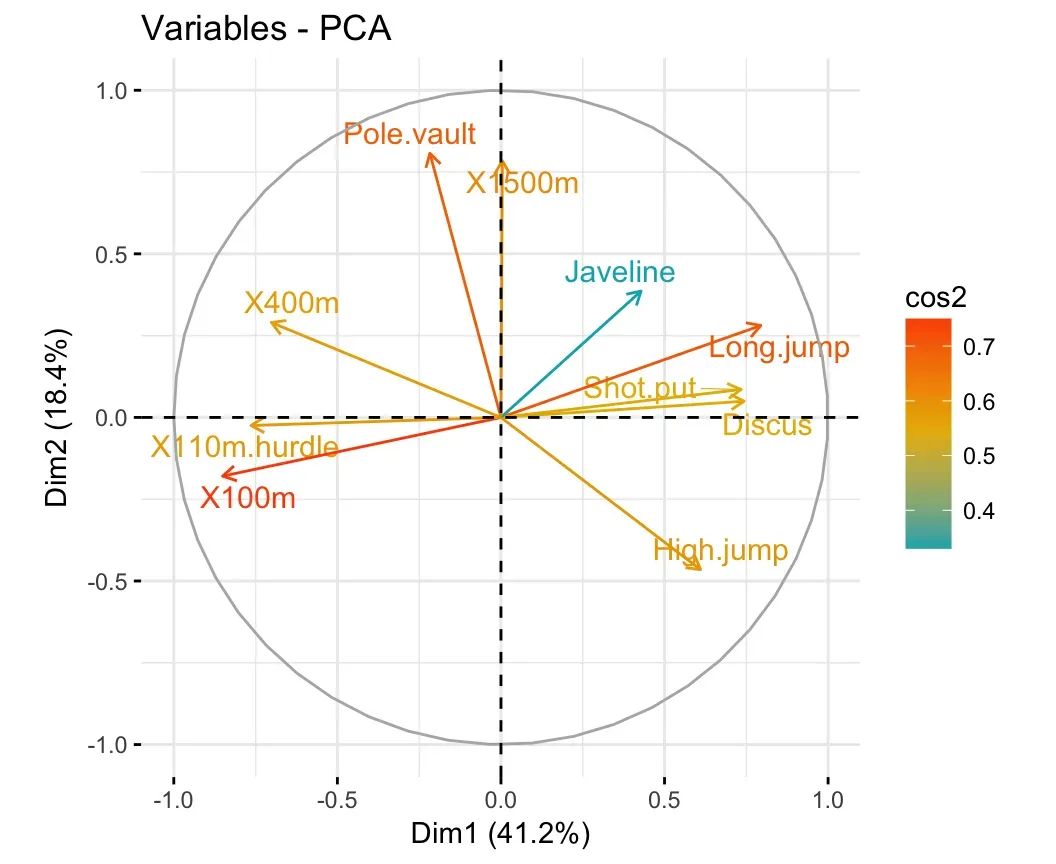
请注意,也可以使用选项 alpha.var = "cos2" 根据变量的cos2值更改变量的透明度。例如,键入以下内容:
# Change the transparency by cos2 values
fviz_pca_var(res.pca, alpha.var = "cos2")变量对PC的贡献
变量对给定主成分变异性的贡献以百分比表示。
• 与PC1相关的变量(即,维度1)和PC2(即,维度2)是解释数据集变异性的最重要因素。
• 与任何PC不相关或与最后一个维度相关的变量是贡献较低的变量,可以删除以简化整体分析。
变量的贡献可以提取如下:
head(var$contrib, 4)
可以使用函数 corrplot() [corrplot package]来突出显示每个维度的最重要变量:
library("corrplot")
corrplot(var$contrib, is.corr=FALSE)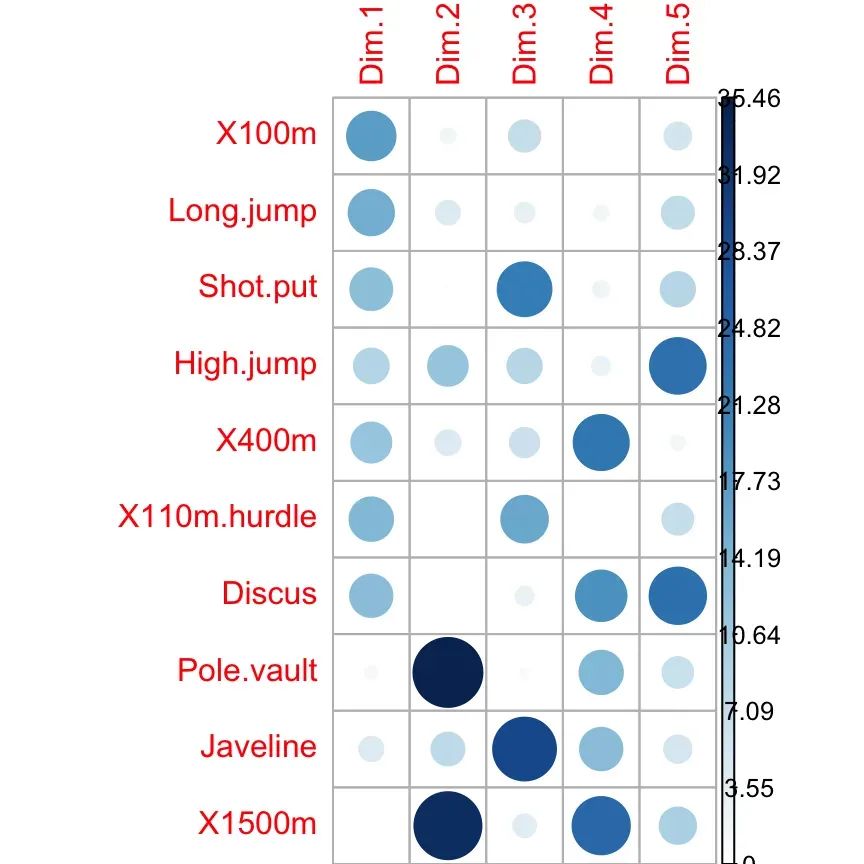
个体图
结果
个体的结果可以使用函数 get_pca_ind() [factoextra package]提取。与 get_pca_var() 类似,函数 get_pca_ind() 提供了一个矩阵列表,其中包含个体的所有结果(坐标、个体与轴之间的相关性、平方余弦和贡献)
ind <- get_pca_ind(res.pca)
ind画图:质量和贡献
fviz_pca_ind() 用于生成个体图。要创建一个简单的绘图,请键入以下内容:
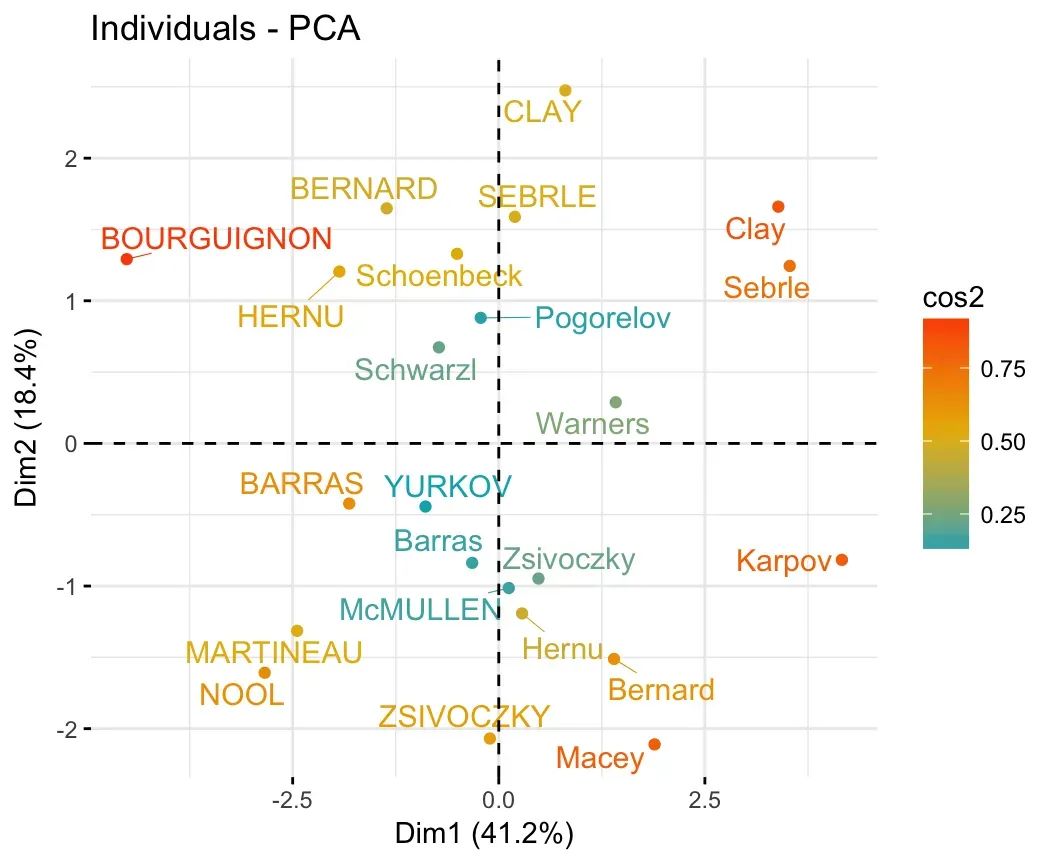
fviz_pca_ind(res.pca)与变量一样,也可以通过cos 2值对个体进行着色:
fviz_pca_ind(res.pca, col.ind = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE # Avoid text overlapping (slow if many points)
)
分组着色
在这里,我们描述如何按组对个体进行着色。此外,我们还展示了如何按组添加浓度椭圆和置信椭圆。为此,我们将使用iris数据作为演示数据集。
iris数据集看起来像这样:

“种属”列将用作分组变量。我们首先计算主成分分析,如下所示:
# The variable Species (index = 5) is removed
# before PCA analysis
iris.pca <- PCA(iris[,-5], graph = FALSE)在下面的R代码中:参数 habillage 或 col.ind 可以用来指定因子变量,用于按组对个体进行着色。
要在每个组周围添加浓度椭圆,请指定参数 addEllipses = TRUE 。参数 palette 可用于更改组颜色。
fviz_pca_ind(iris.pca,
geom.ind = "point", # show points only (nbut not "text")
col.ind = iris$Species, # color by groups
palette = c("#00AFBB", "#E7B800", "#FC4E07"),
addEllipses = TRUE, # Concentration ellipses
legend.title = "Groups"
)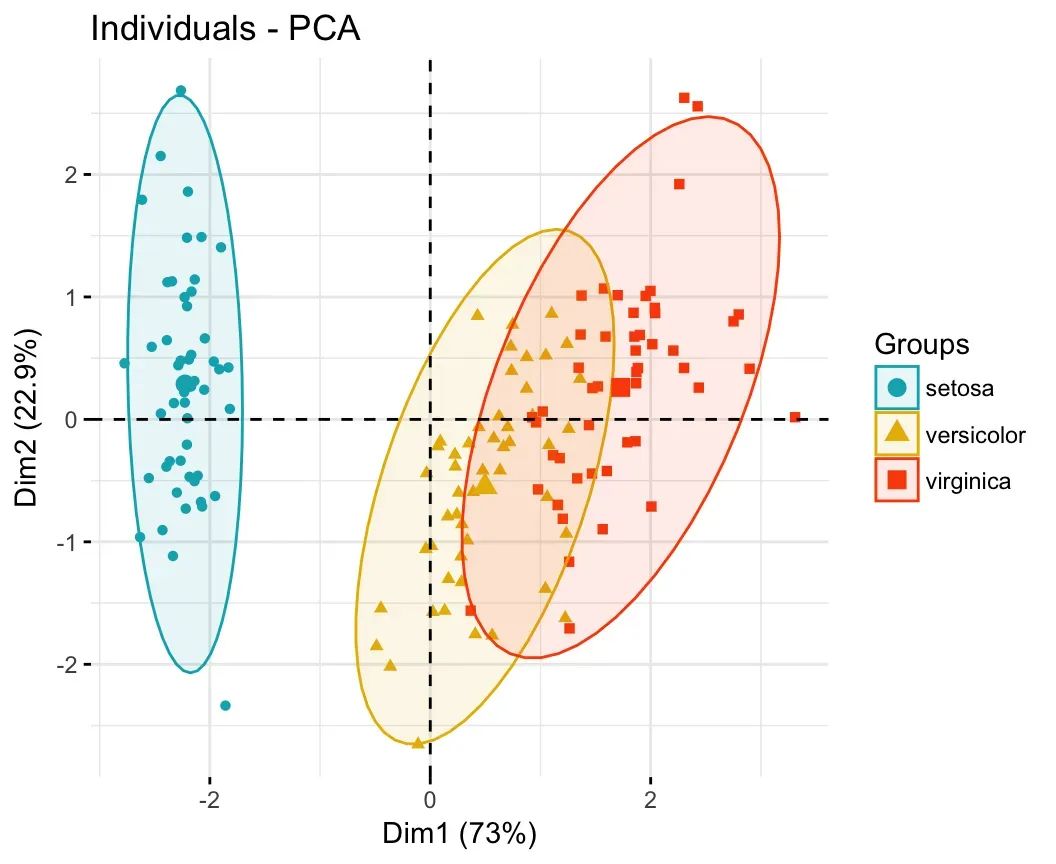
• 要删除组平均点,请指定参数mean.point = FALSE。
• 如果你想要置信椭圆而不是浓度椭圆,使用ellipse.type =“confidence”。
# Add confidence ellipses
fviz_pca_ind(iris.pca, geom.ind = "point", col.ind = iris$Species,
palette = c("#00AFBB", "#E7B800", "#FC4E07"),
addEllipses = TRUE, ellipse.type = "confidence",
legend.title = "Groups"
)请注意,palette允许的值包括:
• “grey”表示灰色调色板;
• brewer 调色板,例如“Rdbu”、“Blues”、.;要查看所有内容,请在R中输入此内容: RColorBrewer::display.brewer.all() 。
• 自定义调色板,例如c(“blue”, “red”);
• 和来自 ggsci R package 的科学期刊调色板,例如:“npg”, “aaas”, “lancet”, “jco”, “ucscgb”, “uchicago”, “simpsons” and “rickandmorty”。
例如,要使用jco(临床肿瘤学杂志)调色板,请键入以下内容:
fviz_pca_ind(iris.pca,
label = "none", # hide individual labels
habillage = iris$Species, # color by groups
addEllipses = TRUE, # Concentration ellipses
palette = "jco"
)本文节选自:
https://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/112-pca-principal-component-analysis-essentials/#r-code
深入学习请阅读原文。
推荐阅读
中国银河生信云平台(UseGalaxy.cn)以“让生信分析更简单”为使命。平台致力于为科研工作者、医疗机构和生物产业技术人员提供全栈式生物信息学分析解决方案。
优先技术响应、定制化工具部署、阶梯式能力培养,请加入「Galaxy生信星球」。咨询微信:usegalaxy 或 galaxy-help

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








