BZOJ0481. 树的重心之砍树Link Cut Centroids

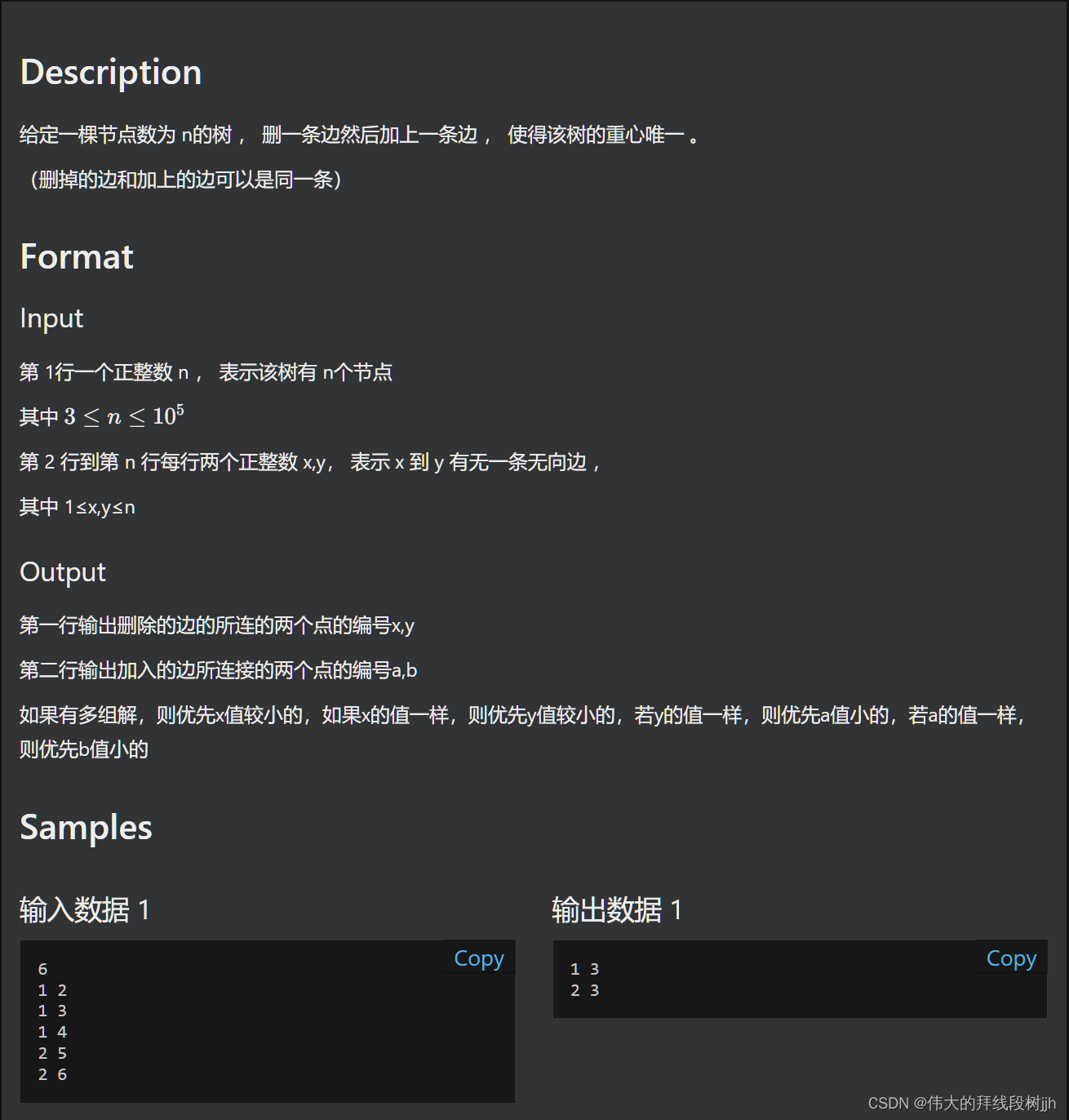
题目

---

思路

分类讨论。

首先当树只有一个重心的时候,我们删掉最小的边再加上原边即可.

再看有两个重心的情况.

显然这棵树必定是类似这样的:

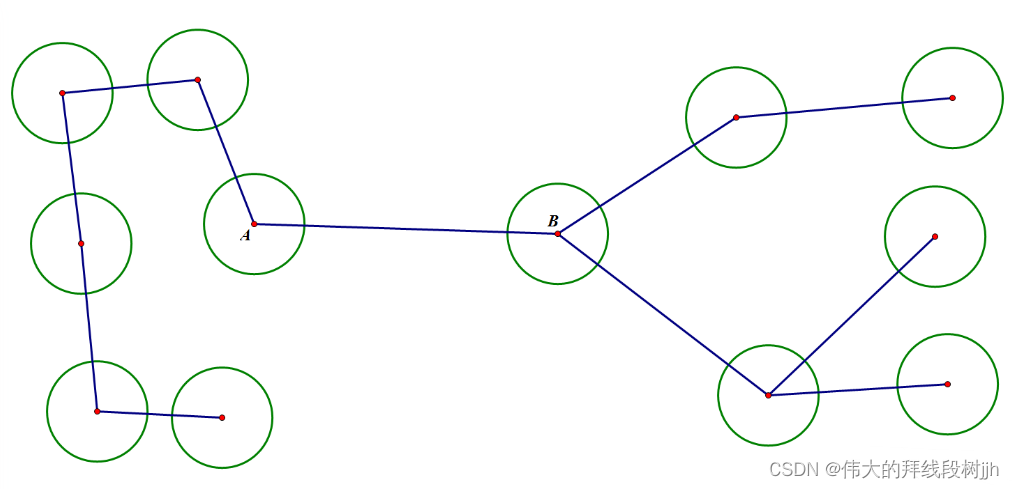
即删掉 A 后,以B 为根的子树是剩下的最大连通块,反之亦然.

那就可以得到一个结论:

• 删掉边 (A,B) 后,两棵树的大小相等.

那我们只要使两棵树的大小不相等,且不使新的点成为重心即可.

那就考虑直接从A 树中取一位编号最小叶子节点,把这个节点与它父亲的边断开,连到 B 的直接儿子中编号最小的节点上去.

这样, A 树的大小变小了,而 B 树的大小变大了,且不会有新的节点成为重心.

那 A 就不再是重心了,而 B 则成为了唯一的重心.

 代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
struct ff
{
  int u,v;
};
ff b[100001];
int n,v[100001],zjd[100001],a[1000001],ans = 1e9,zhong,mnzi = 1e9,mnfa,tzho