#E. 砝码秤重

最新推荐文章于 2025-12-31 19:32:08 发布

原创最新推荐文章于 2025-12-31 19:32:08 发布 · 190 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #动态规划

动态规划专栏收录该内容

15 篇文章

订阅专栏

博客围绕C++使用动态规划解决砝码组合问题展开。定义状态dp[i][j]表示前i种砝码能否组合出重量j，给出状态转移方程，考虑选或不选第k个物品的情况，初始化dp[0][0] = 1，答案为dp[now][i]中为1的个数，并提及后续会给出代码。

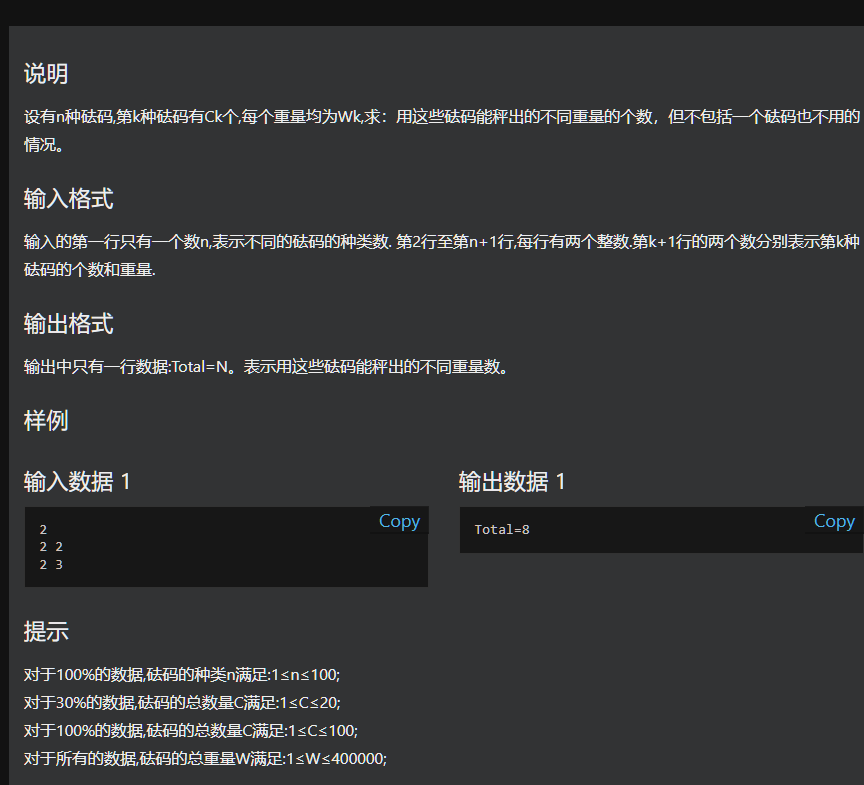
题目

思路

状态

dp[i][j] 表示前 i 种砝码能否组合出重量 j

状态转移方程

dp[i][j] 考虑从哪来

选
for (int k = 1; k <= c[i]; ++k)
{
	// 相当于现在这个砝码的重量就是 k * w[k]
	if (j - k * w[i] >= 0 && dp[i - 1][j - k * w[i]]){
		dp[i][j] = 1;
	}
}
不选
if (dp[i-1][j]) dp[i][j] = 1;

dp[i][j] 考虑到哪去

枚举到 dp[i][j] 时，如果 dp[i][j] 可行

选第 k 个物品，或者不选

选 dp[i+1][j + k * w[i]] = 1

不选dp[i+1][j] = 1

初始化

dp[0][0] = 1

答案

dp[now][i] 中所有为 1的个数

dp[0][0] = 1;
for (int i = 1; i <= n; ++i){
	for (int j = 0; j <= 400000; ++j){
		for (int k = 1; k <= c[i]; ++k){
			// 相当于现在这个砝码的重量就是 k * w[k]
			if (j - k * w[i] >= 0 && dp[i - 1][j - k * w[i]]){
				dp[i][j] = 1;
			}
		}
		不选
		if (dp[i-1][j]) dp[i][j] = 1;
	}
}

代码

#include <bits/stdc++.h>
using namespace std;
int dp[101][580000],w[2000000],c[2000000],n,m,ans,k;
int main()
{
  dp[0][0] = 1;
  cin>>n;
  for(int i = 1; i <= n; i++) cin>>c[i]>>w[i];
  for(int i = 1; i <= n; i++)
    for(int j = 0; j <= 480000; j++)
    {
      for(int k = 1; k <= c[i]; k++)
        if(j - k * w[i] >= 0 && dp[i - 1][j - k * w[i]])
          dp[i][j] = 1;
      if(dp[i - 1][j]) dp[i][j] = 1;
    }
  for(int i = 1; i <= 480000; i++)
    if(dp[n][i])
      ans++;
  cout<<"Total="<<ans;
  return 0;
}