#P05803. 负进制

最新推荐文章于 2025-05-14 19:30:13 发布

原创最新推荐文章于 2025-05-14 19:30:13 发布 · 150 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构

数学专栏收录该内容

44 篇文章

订阅专栏

这篇博客探讨了如何使用短除法处理以-2为基数的情况，特别是当余数为负数时的细节问题。文章通过一个示例代码展示了如何在遇到负余数时调整商和余数，确保在-2进制系统中不出现负数。解决方案是将负余数加2并相应增加商。这个算法对于理解负数在不同进制系统中的处理具有启示意义。

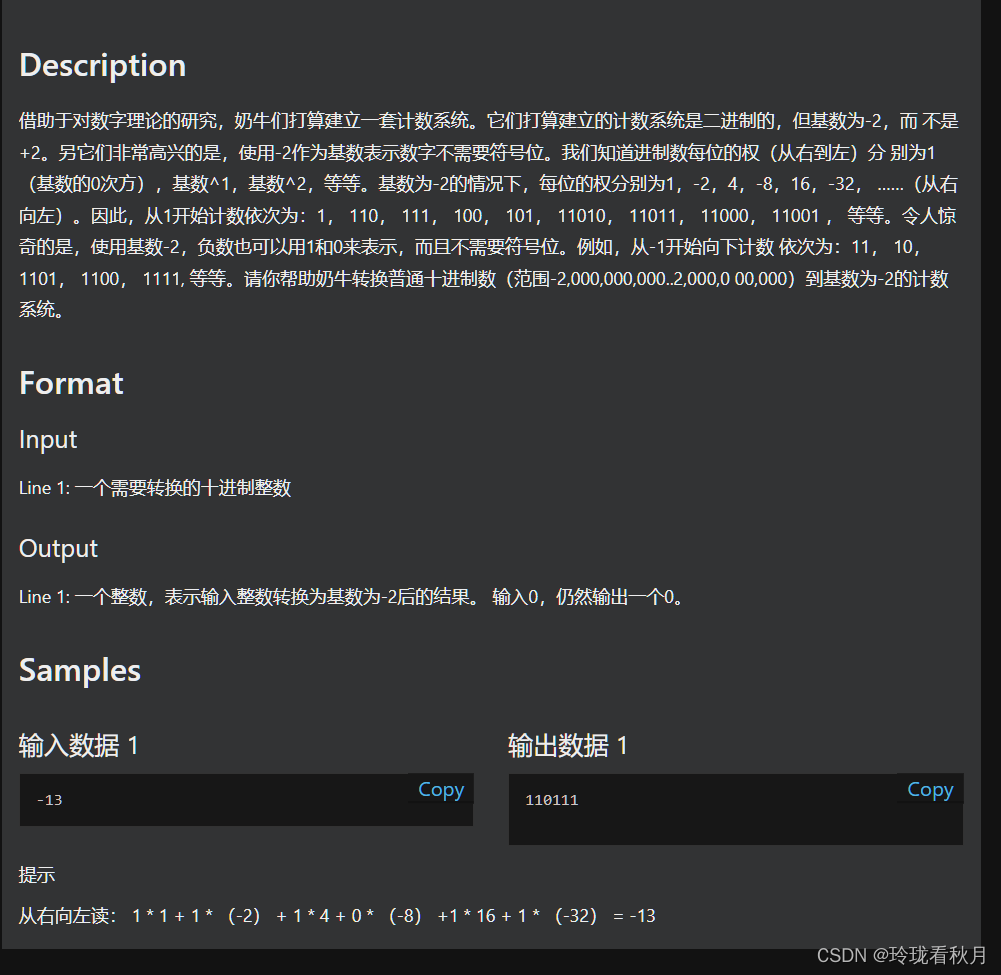
思路:

其实就是普通短除法的举一反三，只不过除数改成了-2而已，不过还是有一些细节要改改（后面会讲）。短除法过程如图(其实是应用了位值原理)

细节问题:在这里假设有a而有时a % -2 < 0该怎么办呢？（比如（-3）%（-2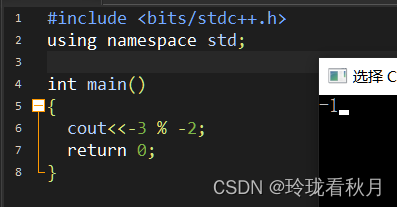））要知道在以-2为基数的进制中是不许数字为负数这种情况出现的。

解决方法：将该余数+2（因为在这里a是% -2,所以如果余数为负则一定==-1,也就是将该余数变成1），再将商+1即可。

代码:

#include <bits/stdc++.h>
using namespace std;
string s;
long long n;
int main()
{
  cin>>n;
  if(n == 0)
  {
  	cout<<0;
  	return 0;
  }
  while(n)
  {
    int c = (n) / (-2),d = (n) % (-2);
    if(d < 0)
    {
      d = 1;
      c++;
    }
    n = c;
    s += d + '0';
  }
  reverse(s.begin(),s.end());
  cout<<s;
  return 0;
}