数据结构综合应用——堆

最新推荐文章于 2021-03-20 17:09:49 发布

原创最新推荐文章于 2021-03-20 17:09:49 发布 · 281 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法

进阶算法专栏收录该内容

16 篇文章

订阅专栏

本文介绍了一种使用对顶堆（一大根堆和一小根堆）动态维护中位数的方法，通过不断调整两个堆之间的平衡来实现实时输出中位数的功能。

动态维护中位数问题，可以用堆，树状数组，线段树等数据结构解决

堆，可以用来进行插入，查询最值，删除最值等操作

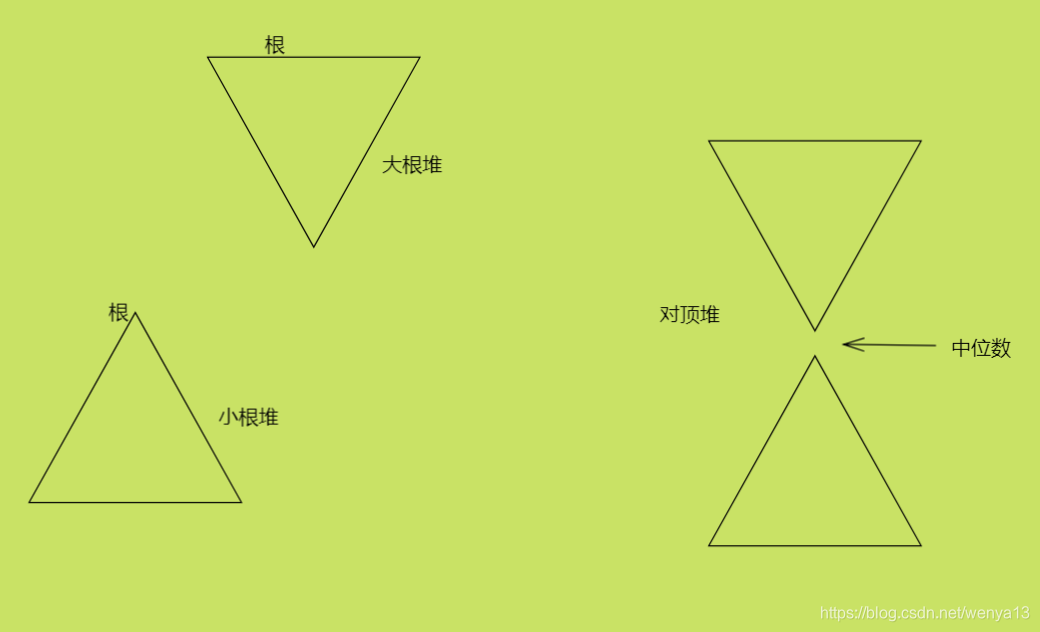
对顶堆：一大根堆和一小根堆，大根堆维护最小值，小根堆维护最大值。

大根堆、小根堆、对顶堆示意图

洛谷1168

题意：每输入奇数个数字，实时输出中位数

解题思路：
定义一个对顶堆，输入第一个数字，并作为中位数输出，
每输入一个数字，大于中位数就插入小根堆；小于等于中位数就插入大根堆
当输入奇数个数字时，维护两堆的平衡，找到中位数并输出。

#include <bits/stdc++.h>
using namespace std;
priority_queue<int, vector<int>, less<int> > q1; //大根堆，基础类型默认是大根堆，默认是less<int>
priority_queue<int, vector<int>, greater<int> >q2; //小根堆

int main() {
	int n; cin >> n;
	
	int mid, t;
	cin >> t;
	mid = t;
	cout << mid << endl;
	
	for(int i = 2; i <= n; i ++) {
		cin >> t;
		if(t > mid) q2.push(t);
		else q1.push(t);
		
		if(i & 1) {
			while(q1.size() != q2.size()) {
				if(q1.size() > q2.size()) {
					q2.push(mid);
					mid = q1.top();
					q1.pop();
				}
				else {
					q1.push(mid);
					mid = q2.top();
					q2.pop();
				}
			}
			cout << mid << endl;
		}
	}
	return 0;
}

学习：
优先队列实现堆的数据结构，first in, largest out的行为特征和操作方法
priority_queue<type, container, functional>
type：数据类型
container：容器类型，（Container必须是用数组实现的容器，比如vector, deque等等，但不能用 list。STL里面默认用的是vector）
functional 是比较方式

“进阶算法”专栏（目录）