算法打卡Day02

今日任务：

1）977.有序数组的平方

2）209.长度最小的子数组

3）59.螺旋矩阵II

977.有序数组的平方

题目链接：977. 有序数组的平方 - 力扣（LeetCode）

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

文章讲解：代码随想录 (programmercarl.com)

视频讲解：双指针法经典题目 | LeetCode：977.有序数组的平方哔哩哔哩bilibili

思路：

1）重新创建一个列表l，

2）采用双指针从两边向中间遍历，比较指针位置的平方大小，大的放入新列表l的末尾，并且相应的指针向中间移动

3）直到两个指针重叠，则退出循环

def sortedSquares(nums: list[int]) -> list[int]:
    k = len(nums) - 1
    left, right = 0, k
    l = list(range(k+1))

    while left <= right:
        if pow(nums[left],2) <= pow(nums[right],2):
            l[k] = pow(nums[right],2)
            right -= 1
        else:
            l[k] = pow(nums[left],2)
            left += 1
        k -= 1

    return l

感想：

这题还比较简单，主要是利用一个双指针，比较指针位置的平方大小，然后从大到小添加到新列表中。

刚开始思考的时候局限于在一个数组内存上实现，废了不少时间。其实比较完直接添加到新列表中即可。后面做题时也是一样，应该先以解决问题为主，然后再进一步优化思路。

209.长度最小的子数组

题目链接：209. 长度最小的子数组 - 力扣（LeetCode）

给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

文章讲解：代码随想录 (programmercarl.com)

视频讲解：

拿下滑动窗口！ | LeetCode 209 长度最小的子数组哔哩哔哩bilibili

方法一：暴力解法，两层循环

思路

1）给一个起始指针i，循环整个数组

2）给一个终止指针j，从起始指针开始往后计算，当总和>=target后，则计算计算两个指针间距（即符合要求的数组长度）

3）定义一个变量，不断更新最小长度

时间复杂度：O(n^2)

空间复杂度：O(1)

暴力解法超时

def minSubArrayLen(target: int, nums: list[int]) -> int:
    i = 0  # 起始指针
    result = len(nums) + 1  # 存储符合要求的最小长度，先给一个比最大长度大的数

    while i <= (len(nums) - 1):
        j = i
        num = 0
        while j <= len(nums) - 1:
            num += nums[j]
            if num >= target:
                subLength = j - i + 1
                result = min(result, subLength)
            j += 1
        i += 1

    return 0 if result == len(nums) + 1 else result

方法二：滑动窗口

思路

1）首先定好起始和终止位置指针，都从0开始

2）移动终止指针，直到区间中元素的累加和大于target

3）记录此时的区间长度，与当前最小长度比较，保留最小长度

4）移动起始指针，直到区间元素的累加和小于target

5）循环操作2)-5)

时间复杂度：O(n)

空间复杂度：O(1)

def minSubArrayLen2(target: int, nums: list[int]) -> int:
    i, j = 0, 0  # 定义起始指针和终止指针
    result = len(nums) + 1  # 存储符合要求的最小长度，先给一个比最大长度大的数
    num = 0  # 区间累加和
    while j <= len(nums) - 1:
        num += nums[j]
        while num >= target:
            subLength = j - i + 1
            result = min(result, subLength)
            num -= nums[i]
            i += 1
        j += 1

    return 0 if result == len(nums) + 1 else result

感想：

暴力法遍历数组，移动初始指针，并循环计算当前初始指针下最小的长度，这里时间复杂度为O(n^2)
而滑动窗口只用一次循环，遍历数组，移动终止指针与开始指针，这样时间复杂度降为O(n)

59.螺旋矩阵II

题目链接：59. 螺旋矩阵 II - 力扣（LeetCode）

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例1:
输入: 3
输出: [ [ 1, 2, 3 ],
       [ 8, 9, 4 ],
       [ 7, 6, 5 ] ]
       
示例2:
输入: 1
输出: [[1]]

文章讲解：代码随想录 (programmercarl.com)

视频讲解：

一入循环深似海 | LeetCode：59.螺旋矩阵II哔哩哔哩bilibili

思路：

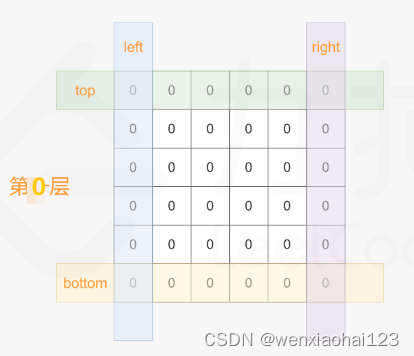
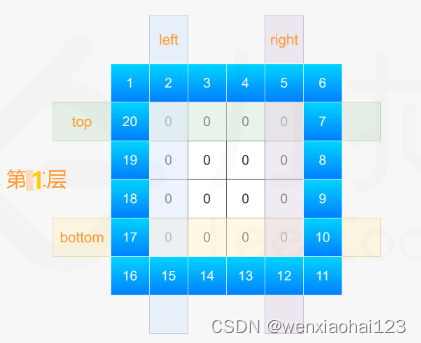
我们可以按螺旋的方向，向矩阵里填充数据，先填最上的横边，再填入最右的竖边，在填入最下面横边，最后填入最左的竖边。
这题最麻烦的地方在于四个顶点的处理，为了统一，我们可以将范围定义为左闭右开。以最外层为例，即每条边填入n-1个数
1）定义上下左右四条边界，从外向里循环的层数（=n//2） 
   ①如果n为奇数，最后中心还有一个数[n//2][n//2],直接将最后的数给它
   ②如果n为偶数，则循环n//2层
2）从外向里循环，按顺时针顺序将1~n^2填进矩阵中
3）每进入下一层时，上下左右边界要相应的向里进1

 

def generateMatrix2(n: int) -> list[list[int]]:
    matrix = [[0] * n for _ in range(n)]  # 定义一个n*n的矩阵
    left, right, top, bottom = 0, n - 1, 0, n - 1  # 定义上下左右边界
    loop = n // 2  # 需要走的圈数
    count = 1
    for l in range(loop):  # l从0开始
        # 第一条边的循环（左上-->右上）
        for col in range(left, right):
            matrix[top][col] = count
            count += 1

        # 第二条边的循环（右上-->右下）
        for row in range(top, bottom):
            matrix [row] [right] = count
            count += 1

        # 第三条边的循环（右下--> 左下）
        for col in range(right,left,-1):
            matrix[bottom][col] = count
            count += 1

        # 第四条边的循环（左下--> 左上）
        for row in range(bottom,top,-1):
            matrix [row][left] = count
            count += 1

        left += 1
        right -= 1
        top += 1
        bottom -= 1

    if n%2 != 0:
        matrix[loop][loop] = count

    return matrix

感想：

这一题在上面思路下，代码中对于一些细节也有很多处理方式，需要格外小心。在我写的第一版代码中，没有定义上下左右边界，而是找出n、l与边界之间的关系，用n和l表示，稍不注意就会弄错，所以在测试容易出现索引溢出，后来按如上方法，代码便清晰不少。