关于用迪杰斯特拉算法求无向图最短路问题

前言

最近在做迪杰斯特拉算法题，为了防止自己再忘了，所以还是记一下为好（惨）

一、如何用此方法求最短路

摘抄自：https://www.jianshu.com/p/01302376b8d7
如何求图中V0到V5的最短路径呢？

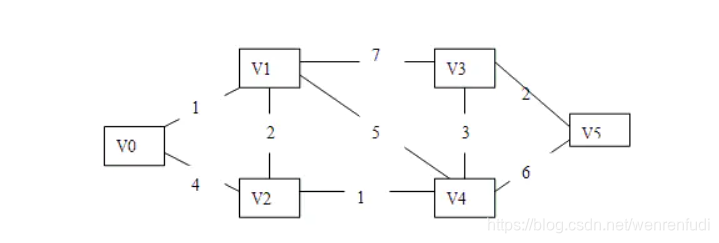
   第一步，根据图来建立权值矩阵：

int[][] W = {
{ 0, 1, 4, -1, -1, -1 },
{ 1, 0, 2, 7, 5, -1 },
{ 4, 2, 0, -1, 1, -1 },
{ -1, 7, -1, 0, 3, 2 },
{ -1, 5, 1, 3, 0, 6 },
{ -1, -1, -1, 2, 6, 0 } }; (-1表示两边不相邻,权值无限大)
例如：W[0][2]=4 表示点V0到点V2的权值为4
W[0][3]=-1表示点V0与V3不相邻，所以权值无限大。
第二步：对V0标号；V0到其它点的路径得到 distance: {0,1,4,-1,-1,-1}; 找到V0到各点中权值最小的那个点（标号的点除外,-1代表无限大），故得到1即对应的下标1，得到V1；对V1标号，然后更改V0通过V1到其它点的路径得到 distance: {0, 1, 3, 8, 6, -1};
第三步：找到distance中权值最小的那个点，（标号的点除外）得到V2,对V2标号，然后更改V0通过V1->V2到其它点的路径得到 distance: {0, 1, 3,8, 4, -1};
第四步：找到distance中权值最小的那个点，（标号的点除外）得到V4,对V4标号，然后更改V0通过V1->V2到其它点的路径得到 distance: {0, 1, 3, 7,4, 10};
第四步：找到distance中权值最小的那个点，（标号的点除外）得到V3,对V3标号，然后更改V0通过V1->V2到其它点的路径得到 distance: {0, 1, 3, 7, 4, 9};
最后只剩下V5没有被标号，就找到V5了。结束！

二、代码模板与分析

代码如下（示例）：

/*关于三个数组：
【1】map数组存的为点边的信息，比如map[1][2]=3，表示1号点和2号点的距离为3
【2】dis数组存的为起始点与每个点的最短距离，比如dis[3]=5，表示起始点与3号点最短距离为5
【3】vis数组存的为0或者1，1表示已经走过这个点。*/
void dijkstra()
{
    int i,j,v,min;
    for(i=0;i<=n;i++)
    {
        vis[i]=0;//初始化为0，表示开始都没走过
        dis[i]=map[1][i];
    }
    for(i=1;i<n;i++)
    {
        min=inf;//无穷大
        for(j=1;j<=n;j++)
        {
            if(!vis[j]&&dis[j]<min)//没被标记，且它们之间的最短距离小于min
            {
                min=dis[j];//更新min
                v=j;//将此时的下标赋值给v
            }
        }
        vis[v]=1;//标记v这个点，表示已经走过
        for(j=1;j<=n;j++)
        {
            if(!vis[j]&&dis[j]>dis[v]+map[v][j])////更新dis的值
                dis[j]=dis[v]+map[v][j];
        }
    }
     printf("%d\n",dis[n]);//到n位置的最短路长度
}

2.一般主函数形式

代码如下（示例）：

int main(){
	int i,j,a,b,c;
	while(~scanf("%d%d",&m,&n)){
		for(i=1;i<=n;i++)
			for(j=1;j<=n;j++)
				if(i==j)
					map[i][i]=0;
				else map[i][j]=map[j][i]=inf;

		for(i=1;i<=m;i++){
			scanf("%d%d%d",&a,&b,&c);
			if(map[a][b]>c) //防止有重边
			map[a][b]=map[b][a]=c;//表示无向图
		}
		dijkstra();
	}
	return 0;
}

三、总结（POJ 2387 Til the Cows Come Home）

贝西在田野里，想回到谷仓，在农夫约翰叫醒她进行早上挤奶之前，尽可能多的睡觉。贝西需要美容觉，所以她想尽快回来。 农夫约翰的田地里有N (2 <= N <= 1000)个地标，唯一编号为1…n .地标1是谷仓；贝西整天站在其中的苹果树林是地标。奶牛在田野里行走，在地标之间使用不同长度的双向奶牛步道。贝西对自己的导航能力没有信心，所以一旦她开始，她总是从头到尾都在跟踪。 给定地标之间的步道，确定贝西必须走多远才能回到谷仓。保证有这样的路线存在。 *第1行:两个整数:T和N *第2行…T+1:每行将一条踪迹描述为三个用空格分隔的整数。前两个整数是步道经过的地标。第三个整数是轨迹的长度，范围为1…100.
有N个顶点和T条边的无向图,现在要问你从1号顶点到N号顶点的最短距离是多少?

#include <iostream>
#include<cstring>
#include<stdio.h>
using namespace std;
#define inf 1<<29
#define MAXV 1005

int map[MAXV][MAXV];
int n,m;
int dis[MAXV];
bool vis[MAXV];
void dijkstra()
{
    int i,j,v,min;


    for(i=0;i<=n;i++)
    {
        vis[i]=0;
        dis[i]=map[1][i];
    }
    for(i=1;i<n;i++)
    {
        min=inf;//无穷大
        for(j=1;j<=n;j++)
        {
            if(!vis[j]&&dis[j]<min)
            {
                min=dis[j];
                v=j;
            }
        }
        vis[v]=1;
        for(j=1;j<=n;j++)
        {
            if(!vis[j]&&dis[j]>dis[v]+map[v][j])
                dis[j]=dis[v]+map[v][j];
        }
    }
    printf("%d\n",dis[n]);
}
int main(){
	int i,j,a,b,c;
	while(~scanf("%d%d",&m,&n)){
		for(i=1;i<=n;i++)
			for(j=1;j<=n;j++)
				if(i==j)
					map[i][i]=0;
				else map[i][j]=map[j][i]=inf;

		for(i=1;i<=m;i++){
			scanf("%d%d%d",&a,&b,&c);
			if(map[a][b]>c) map[a][b]=map[b][a]=c;
		}
		dijkstra();
	}
	return 0;
}