关于遗传算法参数设计及其带来的影响——基于matlab代码实现（附源码及使用说明）（持续更新）

Zeroneeee

已于 2024-11-02 15:17:57 修改

阅读量992

点赞数 27

CC 4.0 BY-SA版权

分类专栏：智能计算文章标签： matlab 开发语言

于 2024-11-02 15:06:45 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_74720002/article/details/143438057

智能计算专栏收录该内容

2 篇文章

订阅专栏

摘要

遗传算法（GA）是借鉴生物界自然选择进化规律的思想，其主要操作包括以下三个基本遗传算子：选择、交叉、变异；采用了概率化寻优的办法，尽管如此，这种随机化操作和传统随机搜索方法是有区别的：遗传操作进行的是高效的、有向的搜索，一般的随机搜索方向是无向搜索。所以，遗传操作的效果和上述三个基本遗传算子所取的操作概率、编码方法、种群大小、初始种群及适应度函数的设定及其区间密切相关。本文将介绍这三种遗传操作基本原理与当前可使用的方法，重点介绍基础操作方法参数设定带来的影响，如选择操作中的轮盘赌、交叉操作中的单点交叉、变异操作中的二进制变异，通过matlab代码进行简单实验去验证各项操作及其相关参数大小对于算法寻优结果的影响。

主要参数与函数说明

%m：输出的最佳个体
%n：输出最佳适应度
%p：输出最佳个体出现代
%q：输出最佳个体自变量值
global G;%当前代
global best_fitness;%历代最佳适应度值
global fitness_avg;%历代平均适应度值矩阵
global best_individual;%历代最佳个体
global best_generation;%最佳个体出现代
global best_fitness_history;


fitness(pop_size,chromo_size);%计算适应度
rank(pop_size,chromo_size);%对个体适应度高低进行排序
selection(pop_size,chromo_size,elitism);%选择操作
crossover(pop_size,chromo_size,elitism);%交叉操作
mutation(pop_size,chromo_size,mutate_rate);%变异操作

初始化

function initilize(pop_size,chromo_size)
%pop_size:种群大小
%chromo_size:染色体长度
%相当于一个矩阵，每行是一个种群，每一列就是对应的染色体序号
global pop;
for i = 1:pop_size
    for j = 1:chromo_size
        pop(i,j) = round(rand);
    end
end
%上面这一部分代码是初始化种群

计算适应度

我的适应度函数的示例是：f(x) = -（x - 1）^2 + 4，在计算适应度之前需要注意的一些事项如下：

首先我们的染色体编码是采用二进制的，但是我们的函数是十进制的，所以我们在计算适应度的时候需要将二进制转换为十进制，这就for循环的作用

转换为二进制之后，就开始计算适应度函数，这里有一个问题需要注意，针对于这个函数，我们把计算结果映射到区间[-1,3]里面，为什么这样映射呢，可以观察到这个函数开口是向下的，在x = 1的时候可以取得最大值4，并且，在[-1，3]这个区间的值变化的比较大，便于我们通过图像来判断遗传算法当前使用情况的优劣

这里还涉及了一个线性映射公式如下：

Matlab代码如下：

%下一部分是计算适应度，里面的函数可以根据具体问题进行修改

function fitness(pop_size,chromo_size)
global fitness_value;
global pop;
global G;
new_lower = -0.5;%设定成-5或者-0.5进行对比
new_upper = 1.5;%设定成5或者1.5进行对比
for i = 1:pop_size
    fitness_value(i) = 0;
end
for i = 1:pop_size
    for j = 1:chromo_size
        if pop(i,j) == 1
            fitness_value(i) = fitness_value(i) + 2^(j - 1);%解码成十进制
        end
    end
    %下面是【-1，3】这个区间的
    %fitness_value(i) = -1 + fitness_value(i) * (3.-(-1.))/(2^chromo_size-1);
    %下面是调试区间的
    fitness_value(i) = new_lower + fitness_value(i) * (new_upper - new_lower) / (2^chromo_size - 1);
    fitness_value(i) = -(fitness_value(i)-1).^2+4;
end

调整适应度区间带来的影响

适应度区间直接影响了遗传算法的搜索空间和收敛特性。增大或缩小区间会影响染色体表示的值范围，从而影响解的精确度或多样性。我们可以尝试几个不同的区间，来验证这些影响：

区间缩小（例如 [-0.5, 1.5]）：将搜索空间变小可能会减少种群的多样性，使算法更快地收敛到局部最优解，但可能会降低找到全局最优解的概率。
区间扩大（例如 [-5, 5]）：扩大搜索区间增加了解的多样性，可能会提高找到全局最优解的机会，但可能需要更多的代数来收敛。

区间缩小时

下图是最早出现最优代（p = 5）的时候，表示第五代就出现了，意味着我们的算法很早就开始收敛达到局部最优解

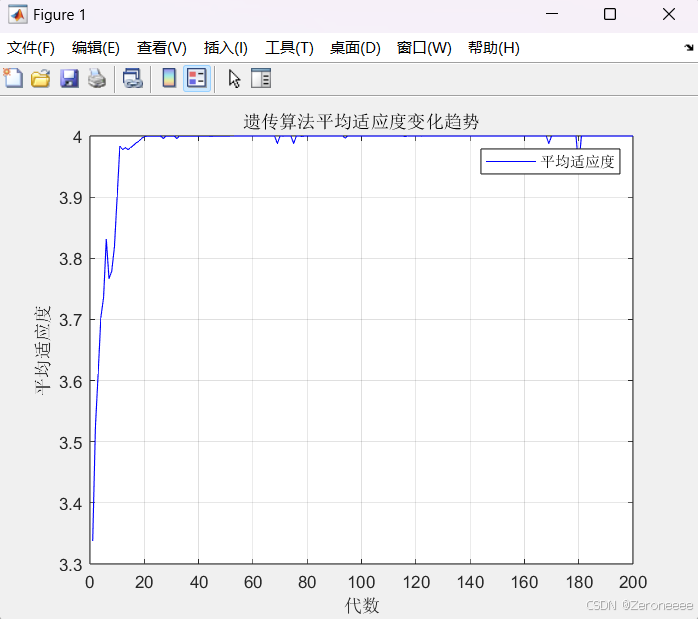
这张图还不是很明显，接下来我们把区间再次缩小到[0.9，1.1]之间，很显然我们这个函数f(x) = -（x - 1）^2 + 4的最大值是当x = 1的时候，这样设定区间意味很早就会开始收敛到接近于4这个数字

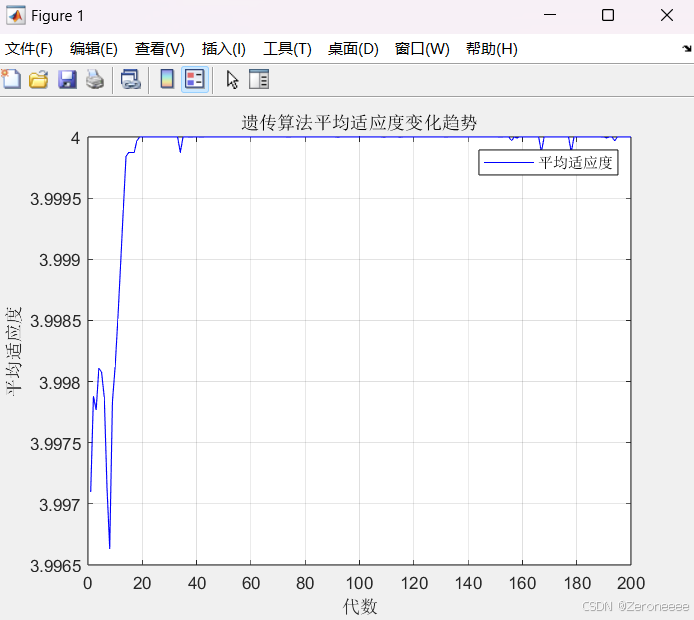
区间扩大时

已知当区间扩大时，我们很有可能需要更多的代数来达到全局最优，于是这里我在扩大区间的同时反而把迭代次数200变成50，结果如下图

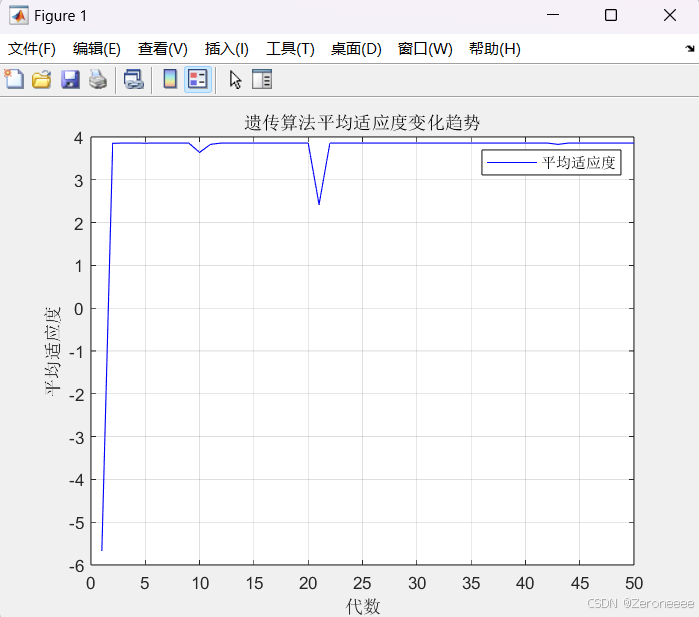
最佳适应度n = 3.8592，离这个函数的最大值还有一些差距

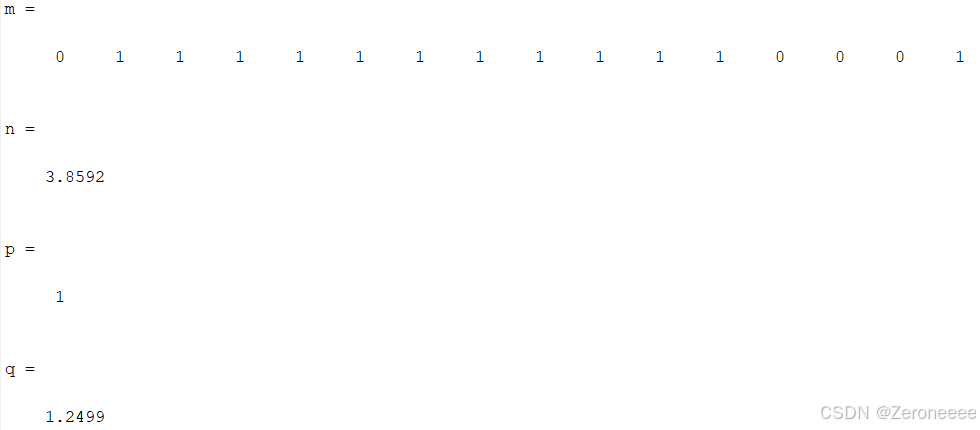
如果我把200代变成1000代，即增加其收敛达到最优的可能性，结果如下：

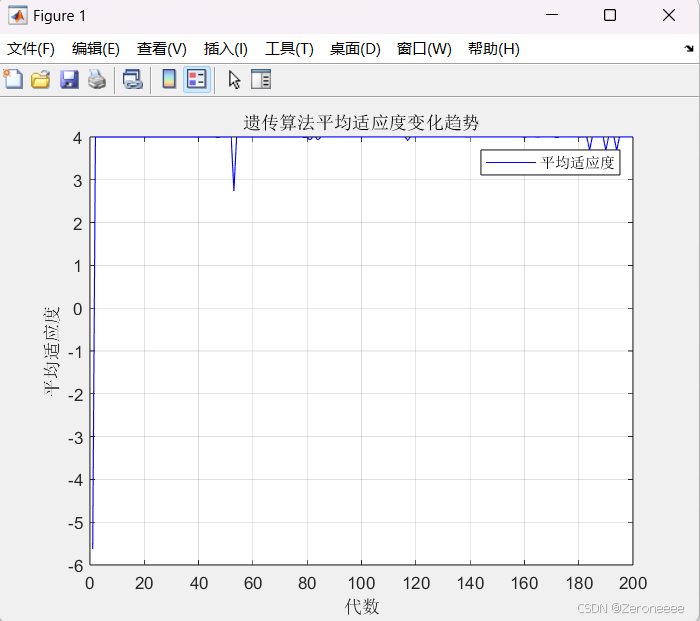
这次我们寻到了最优解n = 4

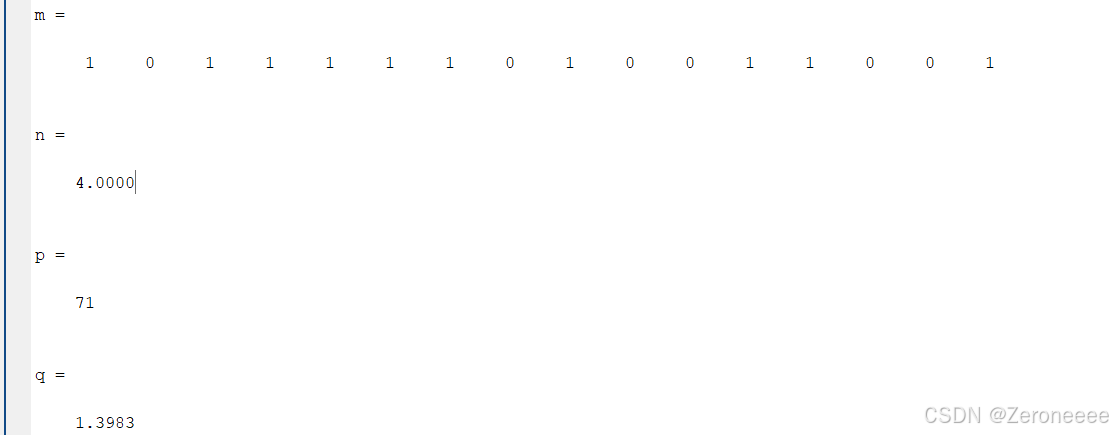
下面是设定的一个较为合理区间的结果

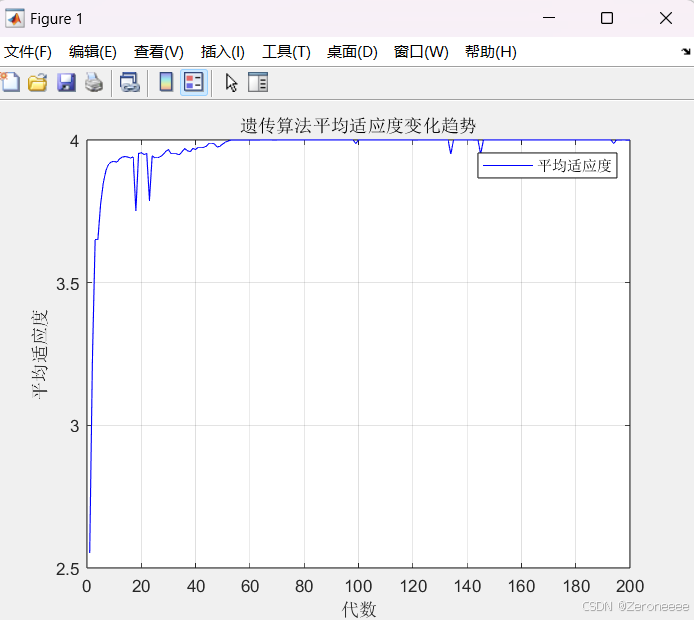
选择操作

选择的基本思想就是“优胜略汰”，目的是为了把优化的个体直接遗传给下一代或者通过配对交叉产生新的个体再遗传给下一代，所以这里还添加了一个对适应度高低进行排序的函数，这样做的目的是为了保存最佳个体。

根据适应度排序并保存最佳个体的函数代码如下：

%下面就是对个体按照其适应度高低进行排序，这样做的目的就是便于保存最佳个体

function rank(pop_size,chromo_size)
global fitness_value;%当前代适应度矩阵
global fitness_table;%
global fitness_avg;%历代平均适应度矩阵
global best_fitness;%历代最佳适应度
global best_individual;%历代最佳个体
global best_generation;%最佳个体出现代
global pop;%种群矩阵
global G;%当前代数的变量
for i = 1:pop_size
    fitness_table(i) = 0.;
end
min = 1;
temp = 1;
temp1(chromo_size) = 0;
for i = 1:pop_size
    min = i;
    for j = i+1:pop_size
        if fitness_value(j)<fitness_value(min);
            min = j;
        end
    end
    if min ~= i% '~'表示非的意思
        temp = fitness_value(i);
        fitness_value(i) = fitness_value(min);
        fitness_value(min) = temp;
        for k = 1:chromo_size
            temp1(k) = pop(i,k);
            pop(i,k) = pop(min,k);
            pop(min,k) = temp1(k);
        end
    end
end
for i = 1:pop_size
    if i==1
        fitness_table(i) = fitness_table(i) + fitness_value(i);
    else
        fitness_table(i) = fitness_table(i - 1) + fitness_value(i);
    end
end
fitness_table
fitness_avg(G) = fitness_table(pop_size)/pop_size;
if fitness_value(pop_size) > best_fitness
    best_fitness = fitness_value(pop_size);
    best_generation = G;
    for j = 1:chromo_size
        best_individual(j) = pop(pop_size,j);
    end
end

目前常用的选择算子方法及其基本思想可以参考下面这个博客：进化计算-遗传算法之史上最全选择策略_遗传算法选择-优快云博客

我们这里用的示例是最简单也是最常用的选择方法：赌轮选择法

%下面是轮盘赌选择操作

function selection(pop_size,chromo_size,elitism)
global pop;
global fitness_table;
for i = 1:pop_size
    r = rand * fitness_table(pop_size);
    first = 1;
    last = pop_size;
    mid = round((last + first)/2);
    idx = -1;
    while (first<=last) && (idx == -1)
        if r > fitness_table(mid)
            first = mid;
        elseif r < fitness_table(mid)
            last = mid;
        else
            idx = mid;
            break;
        end
        mid = round((last + first)/2);
        if(last - first) == 1
            idx = last;
            break;
        end
    end
    for j = 1:chromo_size
        pop_new(i,j) = pop(idx,j);
    end
end
if elitism
    p = pop_size - 1;
else
    p = pop_size;
end
for i = 1:p
    for j = 1:chromo_size
        pop(i,j) = pop_new(i,j);
    end
end

交叉操作

在自然界生物进化中起核心作用的是生物遗传基因的重组。同样，在遗传算法中起核心作用的是遗传操作的交叉算子。所谓交叉，是指把两个父代个体的部分结构加以替换、重组而生成新个体的操作。通过交叉，遗传算法的搜索能力得以飞速提高。

交叉算子根据编码方式的不同，可以分为实值重组和二进制交叉，我们这个示例用的是二进制编码的方式，所以演示的是二进制交叉中的单点交叉，其余交叉操作及具体可参考下面这个博客

进化计算-遗传算法之史上最直观交叉算子（动画演示)-优快云博客

关于交叉概率的影响

交叉概率太大容易破坏破坏已有的有利模式，随机性增大，容易措施最优个体；交叉概率太小，不能有效地更新种群。交叉概率一般取0.4~0.99

接下来三张图分别是我们正常设定的交叉概率为0.6的情况、设定交叉概率为0.01的情况，与交叉概率为0.99的情况

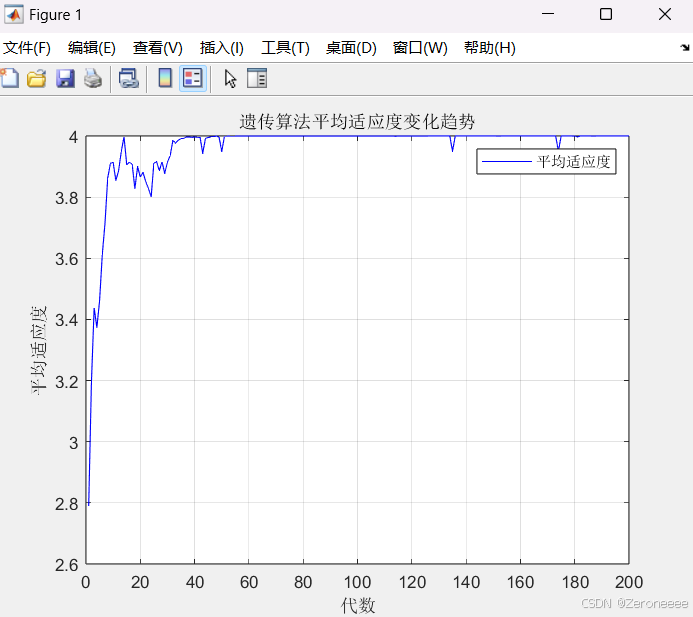
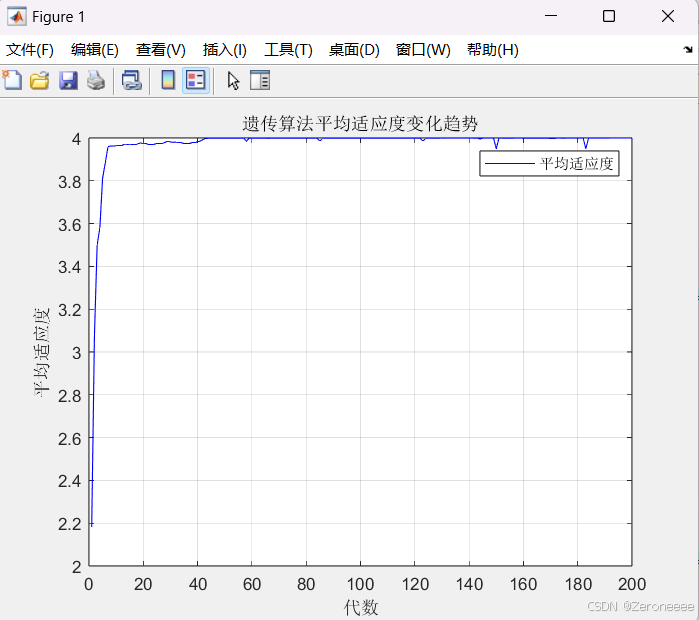
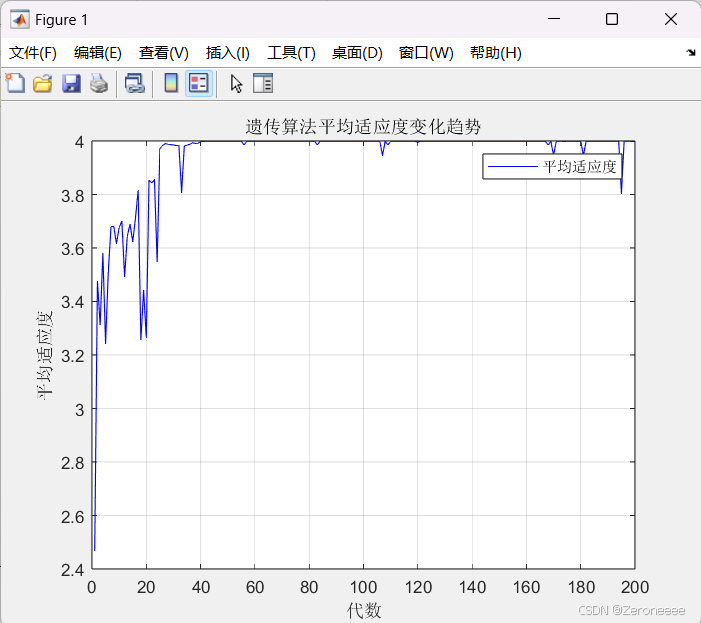
可以看到交叉概率为0.01的时候种群的波动并不大，但是交叉概率为0.99的时候波动会比较大

变异操作

遗传算法（四）——交叉、变异与替换_遗传算法交叉-优快云博客

变异算子的基本内容是对种群中的个体串的某些基因座上的基因值进行变动。过呢据个体编码表示方法的不同，变异算子分为实值变异和二进制变异。

遗传算法引入变异的目的如下：

（1）使遗传算法具有进行局部搜索的能力。当遗传算法通过交叉算子接近最优解邻域时，利用变异算子的这种局部随机搜索能力可以加速其向最优解收敛。显然，这种境况下的变异概率应取较小的值，否则接近最优解的积木块会因为变异遭到破坏。

（2）使遗传算法可维持种群多样性，防止出现未成熟收敛现象。此时收敛概率应取较大值。

变异概率的影响

当变异概率太小的时候，种群的多样性下降的太快，容易导致有效基因的迅速丢失且不容易修补

当变异概率太大的时候，尽管种群的多样性可以得到保证，但是高阶模式被破坏的概率也随之增大。

变异概率一般取0.0001~0.2.

下面是当变异概率很大的情况可以得到的结果：

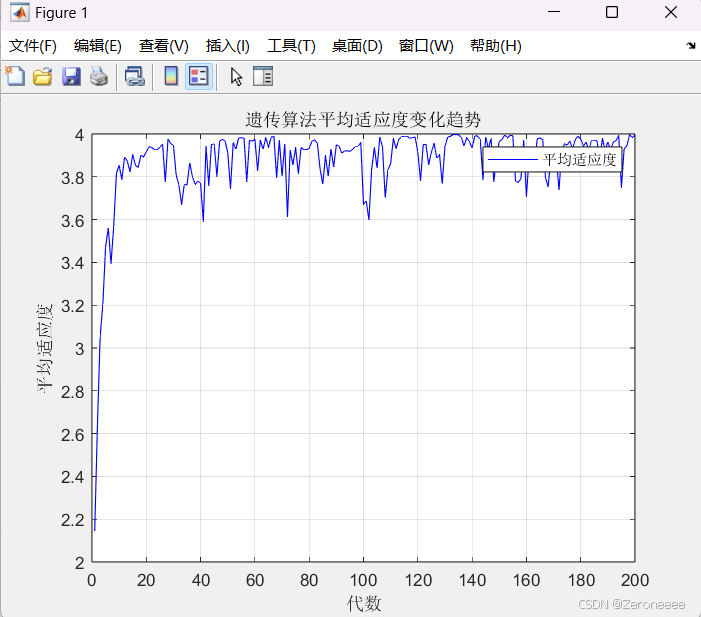
可以看到此时的曲线收敛的并不是很稳定，尽管某些时候可以得到最优解，但是由于变异的发生，随着不断的迭代下去，会突然导致适应度再次下降，并不能稳定下来

下图是经过调整后将变异概率调整至0.01时的图像：

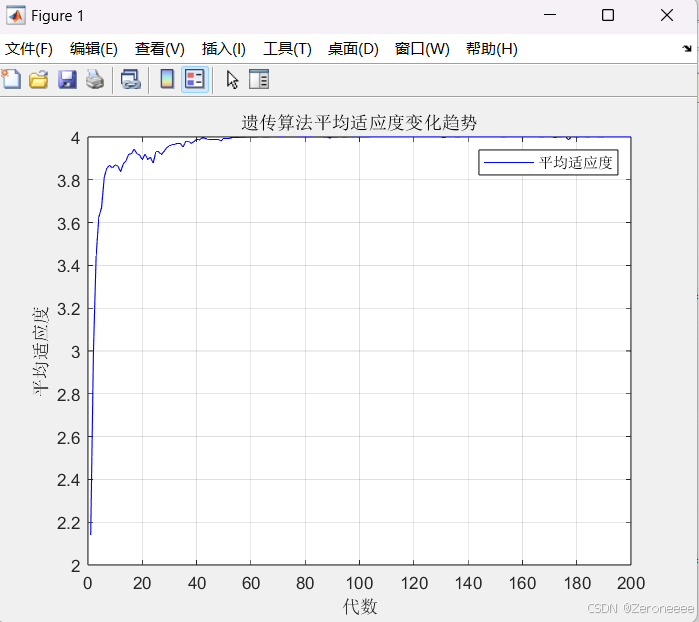
会在最优解附近趋于稳定

总结

总的来说，对于遗传算法的性能有重大影响的六个方面：编码机制、选择策略、交叉算子、变异算子、特殊算子和参数设计（包括种群规模、交叉概率、变异概率等）。此外，遗传算法与差分进化算法、免疫算法、模拟退火算法等结合起来构成的各种混合遗传算法可以综合遗传算法和其他算法的优点，提高运行的效率和求解的质量。

源代码及使用方式

本文代码的运行环境是MATLAB R2023b

源代码如下：

%下面是算法主函数

function [m,n,p,q] = GeneticAlgorithm(pop_size,chromo_size,generation_size,cross_rate,mutate_rate,elitism)
%m：输出的最佳个体
%n：输出最佳适应度
%p：输出最佳个体出现代
%q：输出最佳个体自变量值
global G;%当前代
global best_fitness;%历代最佳适应度值
global fitness_avg;%历代平均适应度值矩阵
global best_individual;%历代最佳个体
global best_generation;%最佳个体出现代
global best_fitness_history;
fitness_avg = zeros(generation_size,1);
disp "启动！！！！"
fitness_value(pop_size) = 0;
best_fitness = 0.;
best_generation = 0;
initilize(pop_size,chromo_size);
for G = 1:generation_size
    fitness(pop_size,chromo_size);%计算适应度
    rank(pop_size,chromo_size);%对个体适应度高低进行排序
    selection(pop_size,chromo_size,elitism);%选择操作
    crossover(pop_size,chromo_size,elitism);%交叉操作
    mutation(pop_size,chromo_size,mutate_rate);%变异操作
end
plotGA(generation_size);
m = best_individual;
n = best_fitness;
p = best_generation;

q = 0.;
for j = 1:chromo_size
    if best_individual(j) == 1
        q = q + 2^(j-1);
    end
end
q = -1 + q*(3.-(-1.))/(2^chromo_size - 1);


function initilize(pop_size,chromo_size)
%pop_size:种群大小
%chromo_size:染色体长度
%相当于一个矩阵，每行是一个种群，每一列就是对应的染色体序号
global pop;
for i = 1:pop_size
    for j = 1:chromo_size
        pop(i,j) = round(rand);
    end
end
%上面这一部分代码是初始化种群

%下一部分是计算适应度，里面的函数可以根据具体问题进行修改

function fitness(pop_size,chromo_size)
global fitness_value;
global pop;
global G;
new_lower = -5;%设定成-5或者-0.5进行对比
new_upper = 5;%设定成5或者1.5进行对比
for i = 1:pop_size
    fitness_value(i) = 0;
end
for i = 1:pop_size
    for j = 1:chromo_size
        if pop(i,j) == 1
            fitness_value(i) = fitness_value(i) + 2^(j - 1);%解码成十进制
        end
    end
    %下面是【-1，3】这个区间的
    fitness_value(i) = -1 + fitness_value(i) * (3.-(-1.))/(2^chromo_size-1);
    %下面是调试区间的
    %fitness_value(i) = new_lower + fitness_value(i) * (new_upper - new_lower) / (2^chromo_size - 1);
    fitness_value(i) = -(fitness_value(i)-1).^2+4;
end



%下面就是对个体按照其适应度高低进行排序，这样做的目的就是便于保存最佳个体

function rank(pop_size,chromo_size)
global fitness_value;%当前代适应度矩阵
global fitness_table;%
global fitness_avg;%历代平均适应度矩阵
global best_fitness;%历代最佳适应度
global best_individual;%历代最佳个体
global best_generation;%最佳个体出现代
global pop;%种群矩阵
global G;%当前代数的变量
for i = 1:pop_size
    fitness_table(i) = 0.;
end
min = 1;
temp = 1;
temp1(chromo_size) = 0;
for i = 1:pop_size
    min = i;
    for j = i+1:pop_size
        if fitness_value(j)<fitness_value(min);
            min = j;
        end
    end
    if min ~= i% '~'表示非的意思
        temp = fitness_value(i);
        fitness_value(i) = fitness_value(min);
        fitness_value(min) = temp;
        for k = 1:chromo_size
            temp1(k) = pop(i,k);
            pop(i,k) = pop(min,k);
            pop(min,k) = temp1(k);
        end
    end
end
for i = 1:pop_size
    if i==1
        fitness_table(i) = fitness_table(i) + fitness_value(i);
    else
        fitness_table(i) = fitness_table(i - 1) + fitness_value(i);
    end
end
fitness_table
fitness_avg(G) = fitness_table(pop_size)/pop_size;
if fitness_value(pop_size) > best_fitness
    best_fitness = fitness_value(pop_size);
    best_generation = G;
    for j = 1:chromo_size
        best_individual(j) = pop(pop_size,j);
    end
end


%下面是轮盘赌选择操作

function selection(pop_size,chromo_size,elitism)
global pop;
global fitness_table;
for i = 1:pop_size
    r = rand * fitness_table(pop_size);
    first = 1;
    last = pop_size;
    mid = round((last + first)/2);
    idx = -1;
    while (first<=last) && (idx == -1)
        if r > fitness_table(mid)
            first = mid;
        elseif r < fitness_table(mid)
            last = mid;
        else
            idx = mid;
            break;
        end
        mid = round((last + first)/2);
        if(last - first) == 1
            idx = last;
            break;
        end
    end
    for j = 1:chromo_size
        pop_new(i,j) = pop(idx,j);
    end
end
if elitism
    p = pop_size - 1;
else
    p = pop_size;
end
for i = 1:p
    for j = 1:chromo_size
        pop(i,j) = pop_new(i,j);
    end
end


%下面是交叉操作，并且是单点交叉操作

function crossover(pop_size,chromo_size,cross_rate)
global pop;
for i = 1:2:pop_size
    if(rand<cross_rate)
        cross_pos = round(rand*chromo_size);
        if or(cross_pos == 0,cross_pos == 1)
            continue;
        end
        for j = cross_pos:chromo_size
            temp = pop(i,j);
            pop(i,j) = pop(i + 1,j);
            pop(i + 1,j) = temp;
        end
    end
end


%下面是变异操作，是单点变异

function mutation(pop_size,chromo_size,mutate_rate)
global pop;
for i = 1:pop_size
    if rand<mutate_rate
        mutate_pos = round(rand*chromo_size);
        if mutate_pos == 0
            continue;
        end
        pop(i,mutate_pos) = 1 - pop(i,mutate_pos)
    end
end

%下面是打印算法迭代过程



function plotGA(generation_size)
    % generation_size 是迭代次数
    global fitness_avg;           % 历代平均适应度
    % global best_fitness_history;   % 历代最佳适应度
    
    % 横坐标为代数，纵坐标分别是平均适应度和最优适应度
    x = 1:1:generation_size;
    y_avg = fitness_avg;          % 平均适应度曲线
    % y_best = best_fitness_history; % 最优适应度曲线

    % 绘制平均适应度曲线
    plot(x, y_avg, '-', 'Color', 'b', 'DisplayName', '平均适应度');
    hold on;

    % 绘制最优适应度曲线
    %plot(x, y_best, '-x', 'Color', 'r', 'DisplayName', '最优适应度');
    
    % 添加网格、标题和标签
    grid on;
    title('遗传算法平均适应度变化趋势');
    xlabel('代数');
    ylabel('平均适应度');
    
    % 添加图例
    legend show;

    
    % 在图中标注最终最优适应度
    % text(generation_size, y_best(end), ...
    %      sprintf(' 最优适应度 = %.2f', y_best(end)), ...
    %      'VerticalAlignment', 'bottom', 'HorizontalAlignment', 'right', 'Color', 'r');
    % 
    % hold off;






% function plotGA(generation_size)
% %generation_size是迭代次数
% global fitness_avg;
% x = 1:1:generation_size;
% y = fitness_avg;
% plot(x,y)

% elitism = true;
% pop_size = 20;
% chromo_size = 16;
% generation_size = 200;
% cross_rate = 0.6;
% mutate_rate = 0.01;
% [m,n,p,q] = GeneticAlgorithm(pop_size,chromo_size,generation_size,cross_rate,mutate_rate,elitism)

1、创建一个文件：GeneticAlgorithm.m

2、把上述代码粘贴进去

3、然后输入：

elitism = true;
pop_size = 20;
chromo_size = 16;
generation_size = 200;
cross_rate = 0.6;
mutate_rate = 0.01;
[m,n,p,q] = GeneticAlgorithm(pop_size,chromo_size,generation_size,cross_rate,mutate_rate,elitism)

elitism：表示精英挑选，因为我们这里计算适应度之后进行了排序，挑选较好适应度的染色体，true为使用精英挑选，false为不使用，可以自行做实验分析

pop_size：种群规模

chromo_size：染色体长度（采用二进制编码）

generation_size ：迭代次数

cross_rate ：交叉概率

mutate_rate：变异概率

推荐书籍：《智能算法及应用实例分析》——张德丰编著

本文后续还会持续更新，发布到博客一是为了自己后面好补充复习，第二点希望能够对和我一样的初学者有帮助