数据结构(六）：堆，红黑树

堆：

定义：

• 堆 是一种特殊形式的树，堆通常是一个可以被看做一棵树的数组对象(通常也是用数组存储堆)。一个堆有两个特点：1.堆总是一棵完全二叉树(对完全二叉树不理解的可以看数据结构(三））。2.堆中某个结点的值总是大于等于或小于等于其子结点的值(如果堆中某一个结点的值总是大于等于其子结点的值，那么我们把这个堆叫做大顶堆，而根结点是最大值；如果堆中某一个结点的值总是小于等于其子结点的值，那么我们把这个堆叫做小顶堆，而根结点是最小值。）。
• 堆常用于实现优先队列，支持堆排序，找出一个集合当中的最大值或者最小值。
• 升序排列建大顶堆，降序排列建小顶堆。

向上调整和向下调整：

向上调整：在一个堆中当前结点与父结点进行比较大小，如果该堆是一个大顶堆，且当前结点比父结点要大，那么就需要向上调整，把当前结点与父结点交换，让大的结点上去。如果该堆是一个小顶堆，且当前结点比父结点要小，那么也需要向上调整，把当前结点与父结点交换，让小的结点上去。

向下调整：在一个堆中当前结点与子结点进行比较大小，如果该堆是一个大顶堆，且当前结点比子结点要小，那么就需要向下调整，把当前结点与子结点交换，让小的结点下去。如果该堆是一个小顶堆，且当前结点比子结点要大，那么也需要向下调整，把当前结点与子结点交换，让大的结点下去。

堆的基本操作：

1.插入：堆的插入是先把新的结点放在数组的最后面，然后向上调整，直到堆满足定义后停止。

上图：

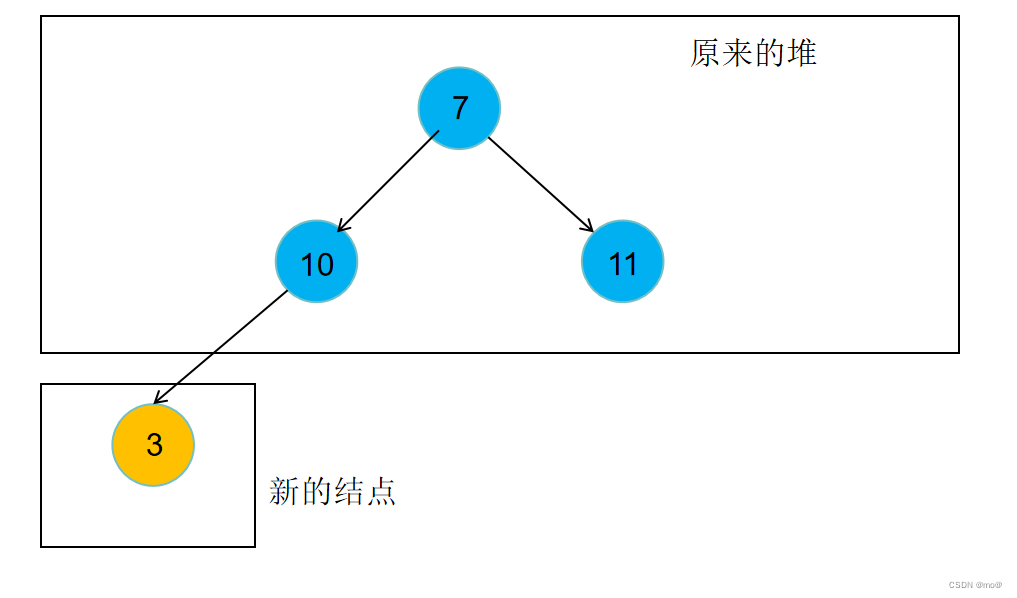
我们看到首先是一个小顶堆，它的数组是[7,10.11],然后想把新的结点3插入。那么新结点3要先与它的父结点进行比较，因为它是小顶堆且3<10，所以结点3和结点10进行交换，然后一直重复该步骤，进行向上调整。结果为：

2.删除：

绝大多数时候在删除的时候都是堆的根结点，因为这就是堆的设计用途(根结点存储最大值或者最小值）。删除了根结点后，可以把最后一个元素移到根结点的位置，这样就满足了完全二叉树的条件，然后再向下调整。

上图：

在这里同样它是一个小顶堆，我们需要删除根结点3，那么在删除后，用最后一个结点10移动到根结点上，然后再找出结点10的左右结点最小的那个结点与它进行交换，重复此步骤，一直向下调整。结果为：

---

---

红黑树：

定义：

红黑树是一种自平衡的二叉查找树，是一种高效的查找树。红黑树具有良好的效率，它可在 O(logN) 时间内完成查找、增加、删除等操作。因此，红黑树应用很广泛。（与AVL树不同的是它并没有AVL树的平衡因子的概念，它只是靠着满足红黑树的性质来维持一种接近平衡的结构，进而提升整体的性能，同时红黑树的插入删除比AVL树更便于控制操作，查找时性能没差别）。

性质：

1. 红黑树的每个结点上都有存储位表示结点的颜色，可以是红(Red)或黑(Black)；
2. 根结点必是黑色；
3. 叶结点都为黑色，且为null（一定是空结点）；
4. 树中不存在两个相邻的红色结点（即红色结点的父结点和孩子结点均不能是红色）；
5. 从任一结点(包括根结点）到其每个叶结点的所有简单路径都包含相同数目的黑色结点，简称黑高。（如果是从一个黑色的结点出发到其的叶结点，那么计算数目的时候要加上这个黑色结点）
6. 从根结点到叶子结点的最长路径不大于最短路径的2倍。那什么是最长路径呢，因为红黑树的性质不允许存在两个相邻的红色结点，那么最长路径肯定是一个黑一个红的样式；而最短路径就是全黑的结点的样式。当从根结点到叶结点的路径上黑色结点相同时，最长路径刚好是最短路径的两倍。
7. 新加入的结点是红色结点。

红黑树的操作：

旋转：

左旋：把某个结点移动到它的结点的右孩子的左子树上，如果原本右孩子它原本存在左子树，那么把该左子树移动到原来这个结点的右子树上，最后让右孩子成为 新的根结点。

右旋：把某个结点移动到它的结点左孩子的右子树上，如果原本左孩子它原本存在右子树，那么把该右子树移动到原来这个结点的左子树上，最后让左孩子成 为新的根结点。

旋转的补充：因为旋转有四种情况，分别为LL，RR，LR，RL，对应的每一种情况的旋转都不同。

插入：

1. 因为红黑树本质上还是一棵二叉排序树，所以可以把红黑树当成一棵二叉排序树将结点插入，如果插入后不破坏红黑树的性质，比如：被插入的结点的父结点为黑色的结点，且插入后满足红黑树性质，那么结束。
2. 如果被插入的结点的父结点是红色的结点，且插入的结点的叔叔结点也是红色的结点，那么只需要变色即可。过程为：先把父结点和叔叔结点设置为黑色结点，再将祖父结点设置为红色，再从祖父结点开始继续操作变色(被插入结点是一定存在叔叔节点的,即使叔叔节点为空，那么它也是一个黑色的空结点。且被插入节点是一定存在非空祖父结点的)。因为插入的结点是红色的结点，那么要考虑会不会存在两个相邻的红色结点，从任一结点(包括根结点）到其每个叶结点的所有简单路径是否包含相同数目的黑色结点，通过变色的方式，使结构满足红黑树的性质。
3. 如果被插入的结点的父结点是红色的结点，但是插入的结点的叔叔结点是黑色的结点，那么需要变色+旋转，使其重新成为一颗红黑树。

删除：

1. 如果删除的是一个红色的结点，直接拿它的子结点补位即可或者不用进行任何调整(比如该红色结点是空结点的上一层的结点）。
2. 如果删除的是一个黑色的结点，因为删除后路径上的黑结点数量少了一个且可能造成相邻的红色结点等情况。那么删除后的情况有：如果该黑色结点有一个孩子为红色结点，那么用这个孩子进行替代，同时给它变色变成黑色。其他情况，就不写了。(因为情况太多了，也很繁杂）