leetcode300.最长递增子序列（记忆化搜索+动规）

leetcode300.最长递增子序列（记忆化搜索+动规）

解法一：记忆化搜索

老样子，在记忆化搜索前看看递归是否能解决问题

先画出递归展开图

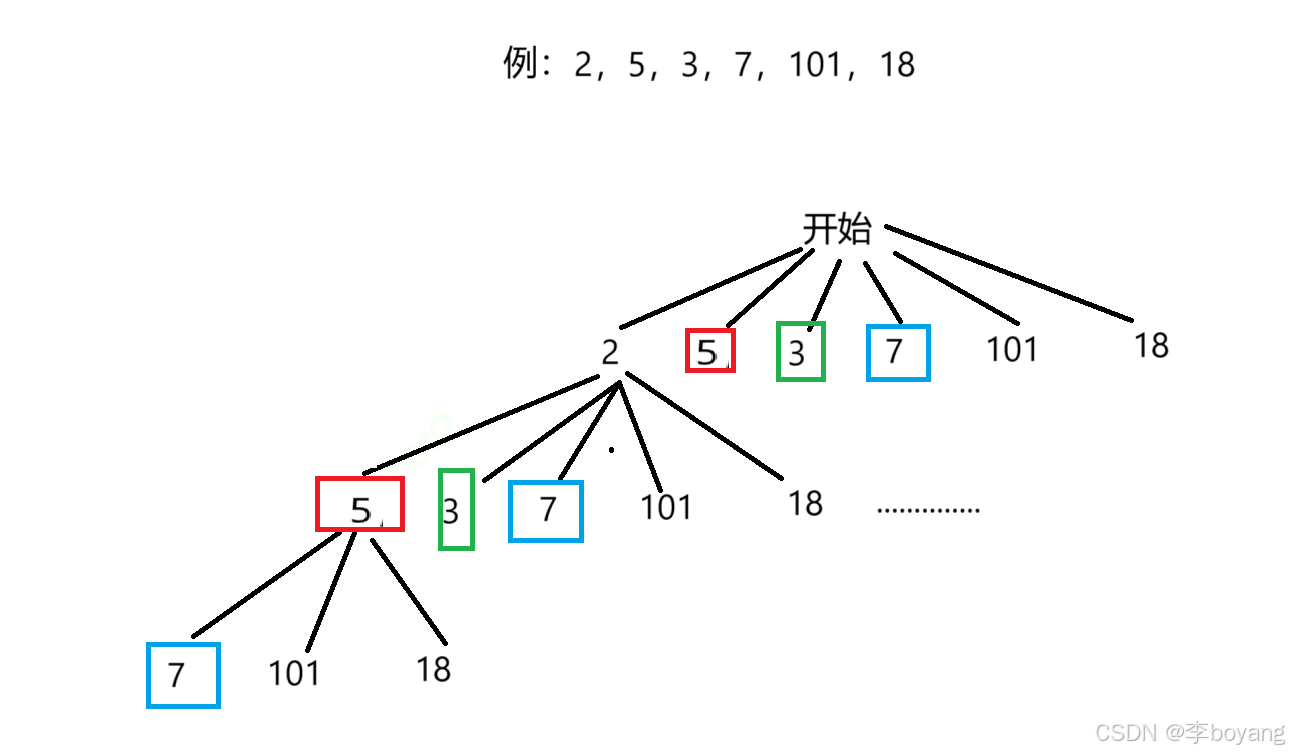
结果依旧是超时，原因还是存在大量重复计算，因此加上“备忘录”

int dfs(int pos,vector<int>& nums,vector<int>& mem)
    {
        if(mem[pos] != 0)
            return mem[pos];
        int ret=1;
        for(int i=pos+1;i<nums.size();i++)
        {
            if(nums[i] > nums[pos])
            ret = max(ret,dfs(i,nums,mem)+1);
        }
        mem[pos] = ret;
        return ret;
    }
    int lengthOfLIS(vector<int>& nums) {
        int ret = 0;
        vector<int> mem(nums.size());
        for(int i=0;i<nums.size();i++)
            ret = max(ret,dfs(i,nums,mem));
        return ret;
    }

解法二：动态规划

1. 确定状态表示

   dp[i]：以i位置为结尾的最长递增子序列的长度
   

2. 状态转移方程

   if(nums[i] > nums[j])
   	dp[i] = max(dp[i],dp[j]+1)
   

3. 初始化

   vector<int> dp(n,1)
   

4. 填表顺序

   从左往右
   

5. 返回值

   max(dp[i])
   

代码：

	int lengthOfLIS(vector<int>& nums) 
	{
        int n = nums.size();
        int ret = 1;
        vector<int> dp(n,1);
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[j] < nums[i])
                    dp[i] = max(dp[i],dp[j]+1);
                ret = max(ret,dp[i]);
            }
        }
        return ret;
    }