N皇后问题（dfs理解版）

题目：在n*n的方格棋盘上，放置n个皇后，要求每个皇后不同行、不同列、不同对角线（本例考虑了副对角线，有些题目不考虑）。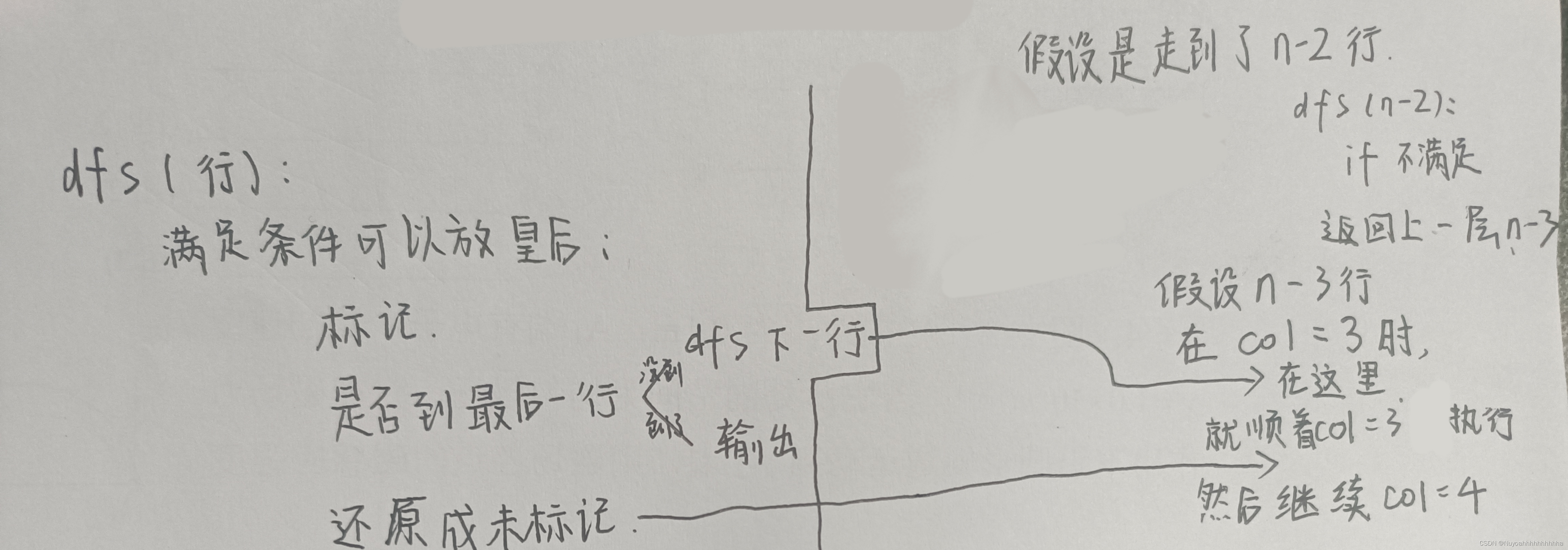

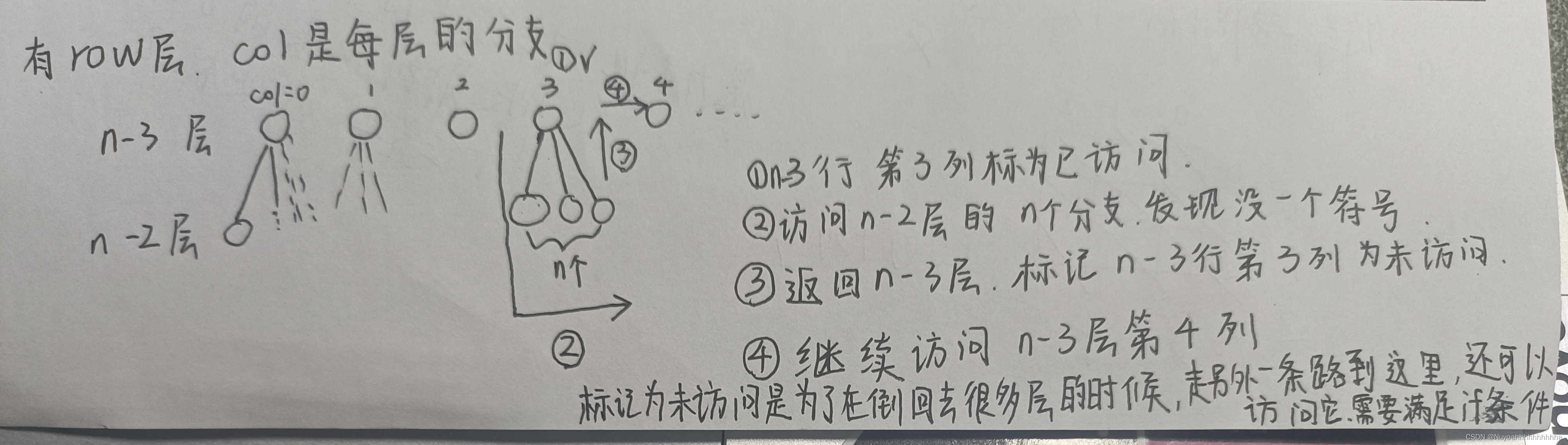
回溯（还原现场）理解：走到头发现走不通了（某个row进行dfs的时候没有一个col满足条件了）返回上一层，在上一层走没走完的for循环，因为上一层的时候，标记了这个位置，进入下一层，没有进行后面回溯的代码，所以发现这条路走不通的时候返回上一层，把走的前面那一步标记为未访问，上一层for循环去搜索下一个col。

n=int(input())
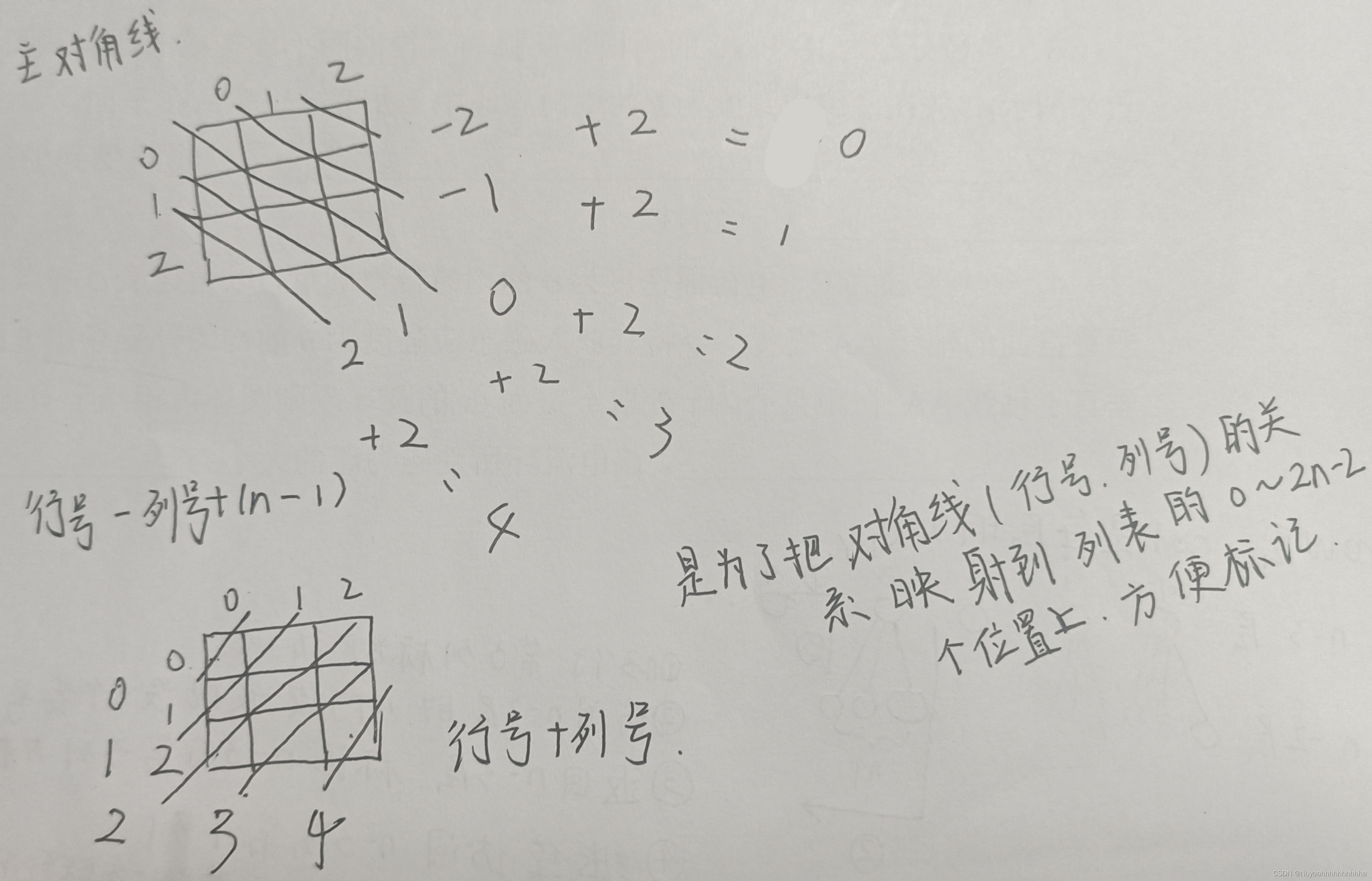
zhu=[0]*(2*n-1)#主对角线，0表示没被标记
fu=[0]*(2*n-1)#副对角线
cols=[0]*n#列需要标记而行不需要，它是一行一行进行dfs的
rows=[-1]*n#-1表示没放皇后，0-(n-1)表示皇后在该行所在的列数
cnt=0#计数器，表示方法数
def dfs(row):
          global cnt
          for col in range(n):
                    if zhu[row-col+n-1]==0 and fu[row+col]==0 and cols[col]==0:#用and,只有主对角线，副对角线，列数都没有被标记才可以搜索
                              zhu[row-col+n-1]=1#满足条件就标记
                              fu[row+col]=1
                              cols[col]=1
                              rows[row]=col
                              #表示第row行，第col列放置皇后
                              if row<n-1:
                                        dfs(row+1)
                              else:
                                        printqueen()
                                        cnt+=1
                              zhu[row-col+n-1]=0
                              fu[row+col]=0
                              cols[col]=0
                              rows[row]=-1
                            
def printqueen():
          for i in range(n):
                    for j in range(n):
                                       if rows[i]==j:
                                                 print('Q',end=' ')
                                       else:   print('0',end=' ')
                    print()
          print()
                    
dfs(0)
print(cnt)