E - Maximize Rating

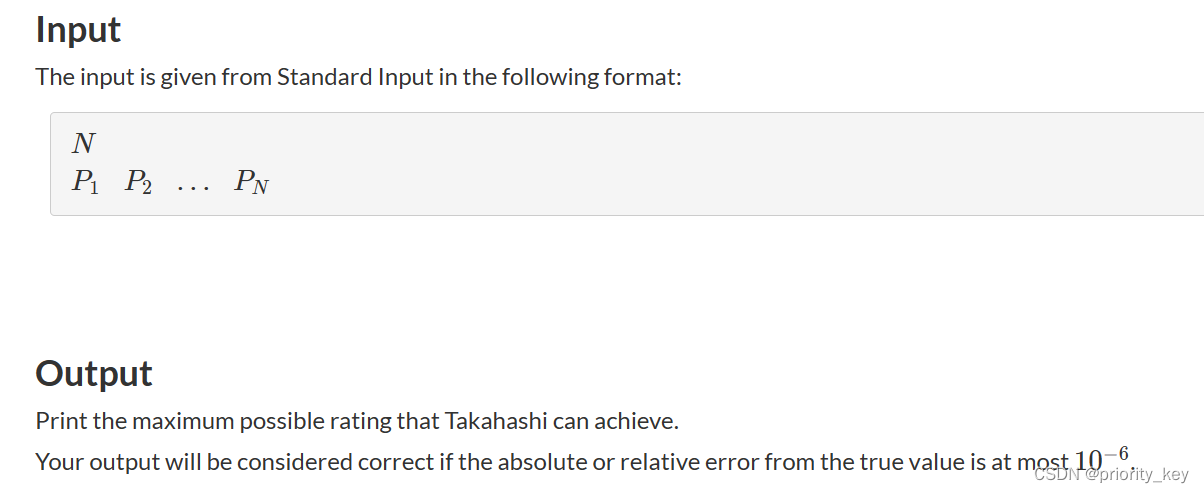
题目要求
这个式子的最大值,其中k为选择比赛的数量, (Q1,Q2,…,Qk) 是所选比赛按参赛顺序排列的成绩,并且必须在不改变初始顺序的情况下进行选择。
式子中要求的变量实际上只有减号右边的分子,不难想到枚举k(1~n),可以O(n^2)解决,dp[i][j]表示前i场比赛选了j场的最大值,
i=j,当k=j的时候,就可以相当于把Qk提出,即pi;再在整个式子中提出一个0.9,就得到dp[i][j] = dp[i - 1][j - 1] * 0.9 + p[i],由于Q的特殊性,实际上所又比赛都只有选与不选两种情况。得出完整的转移方程:dp[i][j] = max(dp[i - 1][j - 1] * 0.9+ p[i], dp[i - 1][j])。
#include <bits/stdc++.h>
#define SQR(x) fixed << setprecision(x)
using namespace std;
using ll = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
const double p0 = 0.9;
vector<double> p(n + 1);
for (int i = 1; i <= n; i++) {
cin >> p[i];
}
vector<vector<double>> dp(n + 1, vector<double>(n + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i][j] = max(dp[i - 1][j - 1] * p0 + p[i], dp[i - 1][j]);
}
}
double ans = -1e18, m = 0, p1 = 1;
for (int i = 1; i <= n; i++) {
m += p1;
ans = max(ans, dp[n][i] / m - 1200.0 / sqrt((double)i));
p1 *= p0;
}
cout << SQR(15);
cout << ans << "\n";
return 0;
}







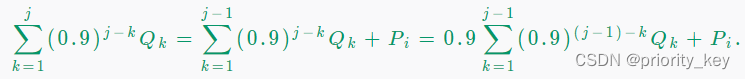


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










