P1525 [NOIP2010 提高组] 关押罪犯
思路:贪心:把影响力最大的两个敌人放在不同监狱,用并查集维护之间的关系(在哪个监狱)。 按照影响里从大到小进行排序,遍历判断两个敌人是否在同一个监狱,如果在同一个监狱,则直接输出当前影响力 否则,将他们分配到不同的监狱(分配原则:敌人的敌人可能是朋友)。
int pre[20005];
int vis[20005]; //存放自己的敌人
struct node {
int x,y,w;
}g[100005];
int find(int f) {
if (pre[f] == f || pre[f] == 0)return pre[f] = f;
else return pre[f] = find(pre[f]);
}
bool cmp(node a, node b) {
return a.w > b.w;
}
void solve() {
int n, m;
cin >> n >> m;
rep(i, 1, m) {
cin >> g[i].x >> g[i].y >> g[i].w;
}
sort(g + 1, g + 1 + m, cmp);
rep(i, 1, m) {
int f1 = find(g[i].x);
int f2 = find(g[i].y);
if (f1 == f2) { //如果在同一个监狱
cout << g[i].w << '\n';
return;
}
if (!vis[g[i].x]) { //把自己的上一个敌人跟现在的敌人放进一个监狱
vis[g[i].x] = g[i].y;
} else pre[find(vis[g[i].x])] = find(g[i].y);
if (!vis[g[i].y]) {
vis[g[i].y] = g[i].x;
} else pre[find(vis[g[i].y])] = find(g[i].x);
}
cout << 0 << '\n';
}P1621 集合
素数筛+并查集 先把所有素数筛出来,再进行合并(用并查集维护集合,有相同的质因子则进行合并)。
const int MAXN = 162280; //随便给的范围
vector<int> primes; //素数表
bool isPrime[MAXN+1];
void getprimes() { //获取素数表
fill(isPrime, isPrime + MAXN + 1, true);
isPrime[0] = isPrime[1] = false;
for (int i = 2; i <= MAXN; i++) {
if (isPrime[i]) {
primes.push_back(i);
for (ll j = (ll) i * i; j <= MAXN; j += i) {
isPrime[j] = false;
}
}
}
}
map<int,int>mp;
int pre[100005];
int find(int f){
if(pre[f]==f||pre[f]==0)return pre[f]=f;
else return pre[f]=find(pre[f]);
}
void solve() {
int n, m, k;
cin >> n >> m >> k;
getprimes();
int ans = 0;
rep(i, n, m) {
int x = i;
int p = 0;
int flag = 1;
while (x >= primes[p]) {
if (x % primes[p] == 0 && primes[p] >= k) {
x /= primes[p];
if (mp[primes[p]]) { //合并
int f1 = find(primes[p]);
int f2 = find(i);
if (f1 != f2) {
pre[f2] = f1;
}
} else {
mp[primes[p]] = 1;
pre[i] = primes[p];
}
} else p++;
}
}
map<int, int> a;
rep(i, n, m) {
if (!a[find(i)])a[find(i)] = 1, ans++;
}
cout << ans << '\n';
}P1955 [NOI2015] 程序自动分析
并查集+离散化
const int N = 1e7+10;
int pre[N];
int find(int f){
if(pre[f]==f||pre[f]==0)return pre[f]=f;
else return pre[f]=find(pre[f]);
}
struct node{
int x,y,e;
}a[N];
bool cmp(node x,node y){
return x.e>y.e;
}
vector<int>pos;
void solve() {
int n;
cin >> n;
rep(i, 1, n) {
cin >> a[i].x >> a[i].y >> a[i].e;
pos.push_back(a[i].x);
pos.push_back(a[i].y);
}
sort(pos.begin(), pos.end());
pos.erase(unique(pos.begin(), pos.end()), pos.end());
sort(a + 1, a + n + 1, cmp);
int flag = 1;
rep(i, 1, n) {
int x = lower_bound(pos.begin(), pos.end(), a[i].x) - pos.begin() + 1;
int y = lower_bound(pos.begin(), pos.end(), a[i].y) - pos.begin() + 1;
x = find(x);
y = find(y);
if (a[i].e == 1) {
if (x != y) {
pre[y] = x;
}
} else {
if (x == y) {
cout << "NO\n";
flag = 0;
break;
}
}
}
if (flag)
cout << "YES\n";
rep(i, 1, 1000000)pre[i] = 0;
pos.clear();
}B. Hamon Odyssey
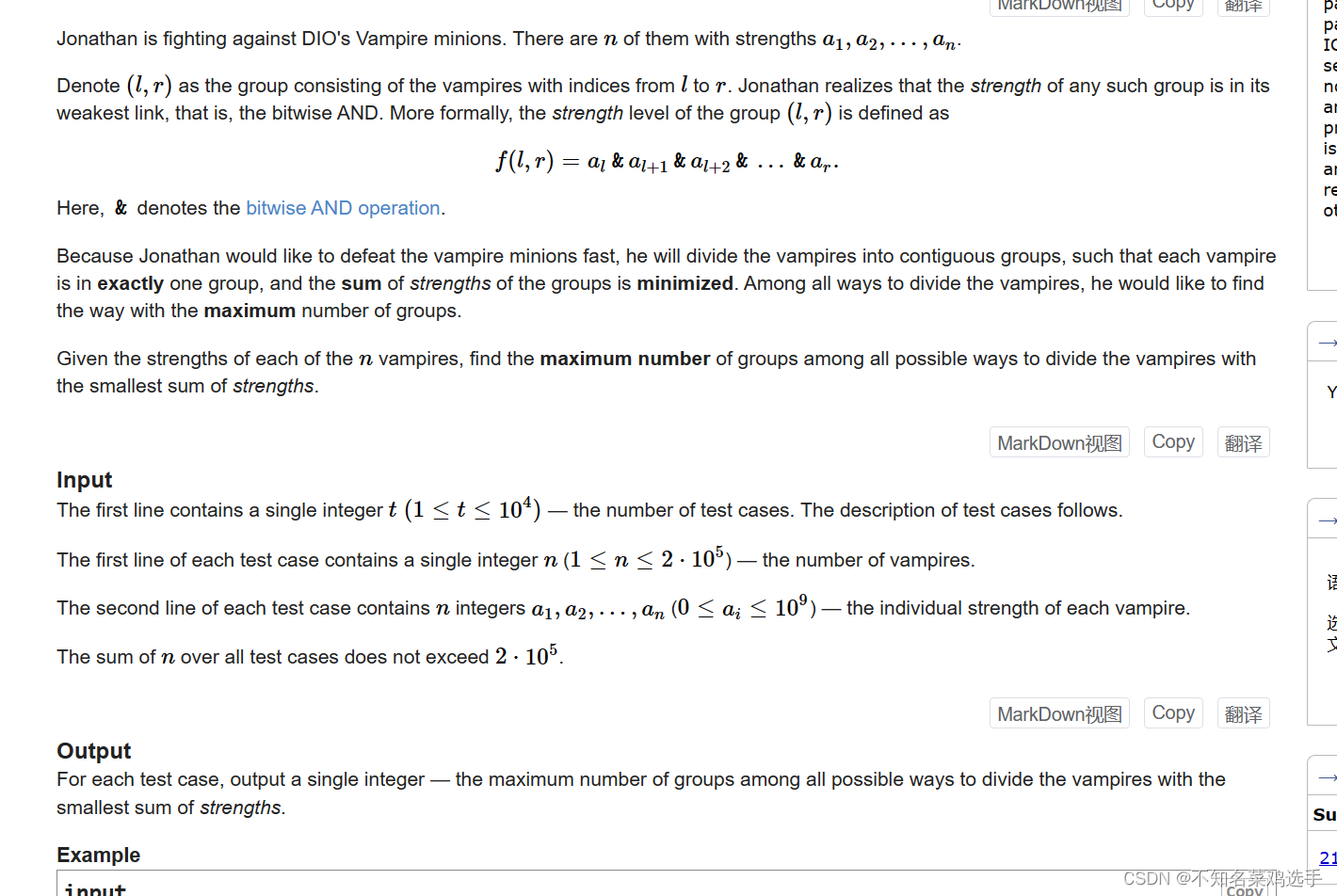
题目大意:给你一个数组a,让你进行分组,每一个组(l-r)的值为a[l]&a[l+1]...&a[r],要求每一个组的值的总和最小并且组的数量最大,输出组的数量。 贪心:要求值最小,我肯定想让它的值等于0,组数最大,把值等于0的分为一个组。 一直&下去,把等于0的分成一组(ans++,从下一个重新开始&),最后结果如果不等于0,而ans等于0的话就输出1。
void solve() {
int n;
cin >> n;
int sum = 0;
int ans = 0;
rep(i, 1, n) {
int x;
cin >> x;
if(!sum)sum = x;
else sum &= x;
// cout<<sum<<' ';
if(!sum)ans++;
}
if(sum&&!ans)cout<<1;
else cout<<ans;
cout << endl;
}C. Vampiric Powers, anyone?

题目大意:给你一个数组a,你可以进行操作:选一个数i(1<=i<=m),生成 a[m+1]=a[i]^a[i+1]^...^a[m],m++。 无限次操作,求生成a[m+1]的最大值 。异或性质:x^y^y=x,所有我们只需要找到一个区间l,r使得a[l]^...^a[r]的值最大,其余的值可以通过再异或一次消掉。 遍历数组相当于枚举右端点,用ret异或起来,并标记每一次ret的值,加入左端点(最前的左端点为0),枚举所有左端点 消掉前面的值,取最大。
int a[100005];
bool vis[300]; //记录左端点
void solve() {
int n;
cin >> n;
rep(i, 1, n)cin >> a[i];
int vis_len = (1 << 8);
int ans = 0;
int ret = 0;
vis[0] = true; //左端点从0开始
rep(i, 1, n) { //枚举右端点
ret ^= a[i];
rep(j, 0, vis_len - 1) { //相当于枚举左端点(把前面的值消掉)
if(vis[j])
ans = max(ans, ret ^ j); //记录最大值
}
vis[ret] = true; //标记左端点
}
cout << ans << endl;
ms(vis, false);
}C - Harmonic Mean
题目大意:给你一个n,问:是否存在n个数的倒数和为1,如果存在输出Yes和那n个数,否则输出No。 思路:因为1/k*(k+1)=1/k-1/(k+1),所以我们可以构建一个(2,6,12...n),但很快就会发现有问题,当n=6时,他已经在前面出现过了,我们可以这样做:n冲突的时候,n-1一定不会冲突,因为前面的序列是i*(i+1)的格式,不存在两个相邻的数,所以当n个数冲突的时候,就先构造n-1个数,n-1个数倒数求和=1,每个数乘以2后倒数求和=1/2,再加上1/2即为1。
#include <bits/stdc++.h>
#define SQR(x) fixed << setprecision(x)
#define ll long long
#define rep(i,p,n) for(int i = p;i <= n; i++)
#define dep(i,p,n) for(int i = n;i >= p; i--)
#define ms(x, y) memset(x, y, sizeof(x))
#define endl '\n'
#define YES "YES"
#define NO "NO"
#define Yes "Yes"
#define No "No"
using namespace std;
void solve() {
int n;
cin >> n;
if (n == 1) {
cout << Yes << endl;
cout << 1 << endl;
return;
}
if (n == 2) {
cout << No << endl;
return;
}
ll a[505] = {0};
a[1] = 2;
ll b[505] = {0};
b[1] = 2;
map<ll, int> mp;
int f = 0;
rep(i, 2, n) {
if (i != n) {
a[i] = (b[i - 1] * (b[i - 1] + 1));
b[i] = b[i - 1] + 1;
} else {
if (!mp[b[i - 1]]) {
a[i] = b[i - 1];
} else {
a[i] = 1;
a[i - 1] /= b[i - 1];
f = 1;
}
}
mp[a[i]] = 1;
}
cout << Yes << endl;
sort(a + 1, a + 1 + n);
if (f) rep(i, 1, n)cout << a[i] * 2 << ' ';
else
rep(i, 1, n)cout << a[i] << ' ';
cout << endl;
}P1896 [SCOI2005] 互不侵犯
这是在看位运算的时候写的,枚举每一行的情况,用二进制表示每一行的状态 每次枚举时要与上一行做比较,判断是否符合条件(有没有国王互相攻击),进行状态转移。
ll f[10][1001][82]; //f[i][j][k]表示在第i行的排列情况j下用了k个国王的方案数,f[0][0][0]=1。
bool vis[1001]; //每一种排列是否符合规则(是否有连续的1)
int w[1001]; //每一个数二进制排列有多少个国王(有多少个1)
void solve() {
int n, m;
cin >> n >> m;
rep(i, 0, (1 << n) - 1) {
for (int j = i; j; j = ((j - 1) & j)) { //计算i的二进制里有多少个1
w[i]++;
}
vis[i] = ((i & (i << 1)) == 0); //判断i的二进制里是否有连续的1
}
f[0][0][0] = 1;
rep(i, 1, n) { //从第一行开始
rep(j, 0, (1 << n) - 1) { //所有排列情况
rep(k, 0, m) { //用了多少个国王
if (f[i - 1][j][k]) { //判断上一行这个状态是否有方案
rep(l, 0, (1 << n) - 1) { //枚举当前的所有排列情况,进行状态转移
//l的二进制有没有国王相互攻击 l与j有没有国王相互攻击
if (vis[l] && ((l & j) == 0) && (((l << 1) & j) == 0) && (((l >> 1) & j) == 0))
f[i][l][k + w[l]] += f[i - 1][j][k];
}
}
}
}
}
ll ret = 0;
rep(i, 0, (1 << n) - 1) { //累加答案
ret += f[n][i][m];
}
cout << ret << endl;
}感觉这几天学习效率有点低,学习也有点拖沓,需要调整一下状态。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










