布隆过滤器——开发必会知识点

后面会更新布隆过滤器（bloom filter）的专栏，包括标准型和目前对其的不同变种，包括涵盖其原理应用优化方案以及未来研究的方向。偏理论（redis或者ORACLE的应用实现看之后有没有时间梳理）这一节会重点介绍标准型BF的使用。下面几讲会谈偏向开发用到的高级的布隆过滤器（想了解更多就关注下博主吧）。

一·标准型BF

布朗过滤器介绍：

是一种用于快速判断一个元素是否属于集合的数据结构，其核心思想是通过多个哈希函数（散列函数）将元素映射到位数组中利用位数的唯一性来表示元素的存在性。标准 BF 的基本操作分为元素查找和元素插入。

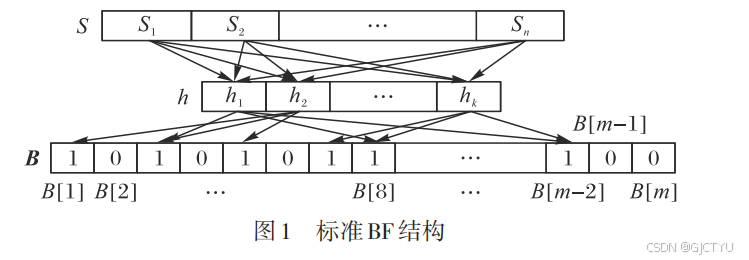
元素插入举例：

S1=100 , 哈希函数分别为h1=xmod7  ,h2=xmod9 h3=xmod6，S1通过哈希函数H1的结果是2，H2的结果是1 ，H3的结果是4。分别映射到位向量B的第2位第1位和第4位，使其存储结果由0变1。S2=50，S2通过哈希函数H2的结果是1，和S1一样，此时B中第1位结果仍然是1。

元素查找举例：

同样根据哈希函数H计算得到 k 个待查找元素的索引值 hi ，如果 ∀i ∈ [1，k]，B 中对应位置都是1，则返回“该元素是集合成员”，否则返回“该元素不是集合成员”。

存在的问题：

聪明的同学已经看出来了，由于空间上的节省且随着集合数据量的增大，位向量中每个位置所映射的元素个数越来越多，从而导致元素查询时发生误判。图 1 中，假设元素 x ∉ S 且 h1 ( x) = 7，h2 ( x) = 5，hn ( x) = 1（其他哈希映射均存在映射地址重复的情况），此时查询结果就会返回“元素属于集合”的错误判断，这种情况发生的概率称为该 BF 的误判率。

布朗过滤器应用场景（列举的其实很少）：

BF在实际的开发应用中是最常用来判断某个元素是否属于集合的工具。下面介绍几个不同方面的使用场景

1. 缓存系统： 在缓存系统中，可以使用布隆过滤器来快速判断一个请求的数据是否在缓存中。这样可以避免频繁地查询缓存存储，从而加快响应速度。

2. 防止缓存穿透： 如果有大量请求访问数据库中不存在的数据，布隆过滤器可以快速拦截这些不存在的请求，避免对数据库造成不必要的查询压力。

3. 垃圾邮件过滤： 在垃圾邮件过滤器中，可以用布隆过滤器存储已知的垃圾邮件特征，以快速识别新的邮件是否为垃圾邮件。

4. 网页爬虫： 在网页爬虫中，布隆过滤器可以用来检测一个URL是否已经被爬取过，避免重复爬取相同的页面，从而节省网络带宽和处理时间。

5. 分布式系统中的唯一性检查： 在分布式系统中，布隆过滤器可以用来检查一个元素是否已经存在于其他节点的数据中，例如分布式缓存或分布式数据库的数据同步过程中。

6. URL 重复检查： 在网址处理程序中，布隆过滤器用于验证新的网址是否已经处理过，避免重复处理相同的网页。

二·拆分向量的布隆过滤器

拆分向量的布隆过滤器依旧是针对标准的布隆过滤器的优化方案，其解决问题是在面对大型数据集和等情况，位向量变大无法完整保存在cache中，在操作中cache的命中率降低，与主存的访存次数变多，性能下降。拆分向量的布隆过滤器核心思想是将数组拆分多个更小的快或层次，更好的利用缓存，减小对主存或硬盘的访存次数，提高查询效率。

2.1并行分区的布隆过滤器（Parallel Partitioned Bloom Filter，PPBF）

并行分区BF将一个过滤器按照 k个哈希函数分为 p个部分，每个部分对应不同的内存块，这样不同部分的查询可以并行进行，互不干扰。可以在查找元素时使用 p 个线程同时进行查找：如果第 i 个部分的查询结果为“真”，则说明元素通过了该部分对应的 k /p 个哈希映射检查，再把该元素放到第下一个部分继续检 查；而如果第 i 个部分的查询结果为“假”，则直接返回“元素 不属于集合”的结果，再把下一个元素放到第 i + 1 个部分中进行检查。

指令访存变为流水线形式，

存储体就相当于BF块，存取周期为T，存取时间为r（这里需要一些计组存储系统的基本概念）

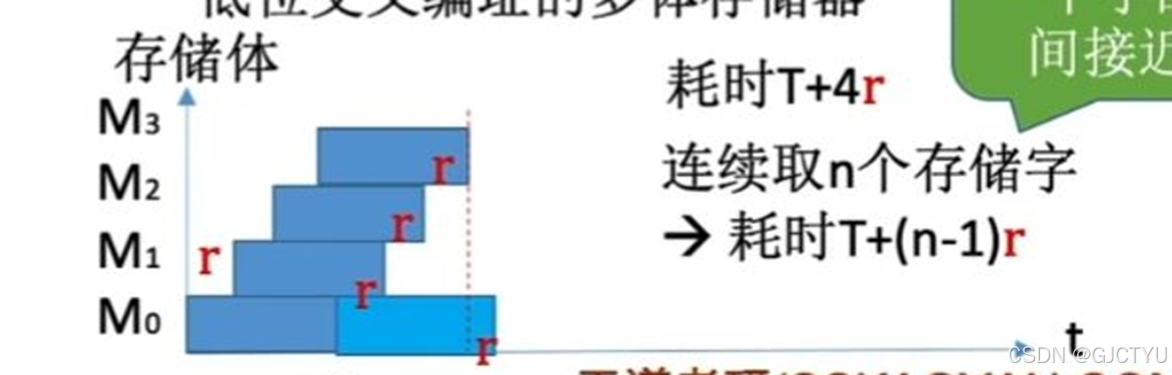
执行过程

2.2缓冲布隆过滤器

缓冲布隆过滤器通过在布隆过滤器外部引入一个缓冲区来解决上述问题。过滤器结构完全置于SSD中（硬盘中）并按照页的大小将其分为若干个子过滤器，在内存中建立于此过滤器数量相等且大小等于块大小的缓冲区。查询操作先在缓冲区进行查找，如果查找不到再查找SSD的子过滤器减少了对SSD的访存次数。类似于计组中虚拟存储器的操作。

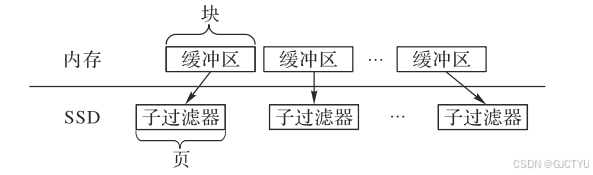
2.3链式布隆过滤器 (Linked Bloom Filter)

在内存中维护一个标准 BF 而不再是一个缓冲区，处理插入操作时，仍然像标准 BF 那样对内存中的过 滤器进行操作，而当内存中过滤器保存的元素数量达到上限 时，将该过滤器转移链接到 SSD 中的子过滤器链表中，然后 在内存中重新构建一个标准 BF，继续保存插入的元素。而 当查询元素时，先查找位于内存中的过滤器。这种方案适合“多插入，少查询”的应用场景。

三·分层的布隆过滤器

需要更精细的数据过滤和查询需求的场景，如ip地址过滤，搜索引擎的索引优化等等的使用场景。

3.1布隆树

布隆树是一棵 d 叉完全树，它的每个节点 都是一个标准 BF，主要解决多集合成员查询问题。一个系统中存在多个集合，每一个集合都有其自身的过滤器，当请求查询一个 Key 对应的 Value 时，检查所有过滤器，如果该 Key 属于其中一个集合，则返回该集合中该 Key 所对应的 Value。

在路由表的自学习算法和路由器过滤中应用较多

3.2持久型BF

解决范围查询，可以用来优化对时间段内某个 IP 地址是否访问过服务器的查询问题

• 类似于线段树（segment tree）的结构，Ⅰ型过滤器使用时间粒度思想对系统的时间范围进行二分划分。
• 每个时间范围划分出的子范围作为树形结构的一个节点，为每个节点分配一个布隆过滤器（BF），负责该时间范围内的元素查询。
• 存储时，只需存储元素内容，而不需要存储时间戳，因为树形结构的每一层都会管理其所负责的时间范围内的元素。
• 为了减少布隆过滤器的数量，文献中规定树形结构的最后一层时间范围不为1，可能是其他的固定时间范围。

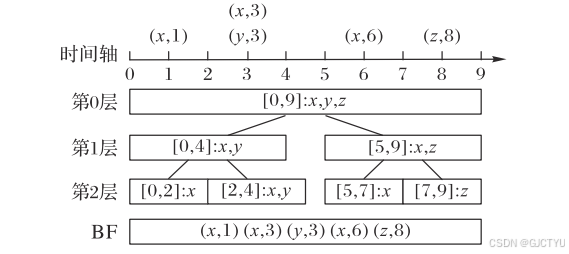
举例 ：

• 存储时，只需要将 IP 地址插入到对应时间段的布隆过滤器中，而不需要存储具体的时间戳。
• 对于查询，例如查询在 0到 9 是否有且什么时候 x 访问过服务器，系统会查询布隆过滤器：
  • 第0层布隆过滤器负责 0 到 9 时间段的查询。
  • 第1层二个布隆过滤器分别负责 0-4 到 5-9 时间段的查询。
• 如果两个布隆过滤器都返回“存在”，那么可以确定在整个 0-4 到 5-9 时间段内确实有 IP1 访问过服务器。
• 以此往下。

四.结语

本文列举的只是不同种类的常见的几种，对应用场景和原理进行了分析，后续内容会继续，求更新点赞关注。