北邮数据结构与算法实践|作业二：迷宫问题

本博客仅供学习交流使用，请勿用于作弊以及用于应付作业，珍惜每一个学习的机会

实验题目

以一个 m×n 的长方阵表示迷宫，0 和1分别表示迷宫中的通路和障碍。设计一个程序,对任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。要求实现以下功能：

1. 以链表作存储结构的栈类型，编写一个求解迷宫的非递归程序。求得的通路以 (i，j) 的形式按通路顺序输出，其中(i，j) 为迷宫中的一个坐标。
2. 求得迷宫中所有可能的通路，并输出最短路径。

以下是仅为一条测试数据：左上角 (0，1)为入口，右下角 (11，12)为出口。

	0	1	2	3	4	5	6	7	8	9	10	11	12
0		入
1
2
3
4
5
6
7
8
9
10
11													出
12

	0	1	2	3	4	5	6	7	8	9	10	11	12
0	1	0	1	1	1	1	1	1	1	1	1	1	1
1	1	0	0	0	0	0	1	0	0	0	0	0	1
2	1	1	1	1	1	0	1	0	1	1	1	0	1
3	1	0	0	0	1	0	1	0	0	0	1	0	1
4	1	0	1	1	1	0	1	1	1	0	1	1	1
5	1	0	0	0	1	0	0	0	1	0	0	0	1
6	1	0	1	0	1	1	1	0	1	0	1	0	1
7	1	0	1	0	1	0	0	0	0	0	1	0	1
8	1	0	1	0	1	0	1	0	1	1	1	0	1
9	1	0	1	0	0	0	1	0	1	0	0	0	1
10	1	0	1	1	1	1	1	1	1	0	1	0	1
11	1	0	0	0	0	0	0	0	0	0	1	0	0
12	1	1	1	1	1	1	1	1	1	1	1	1	1

题目分析与算法设计

题目性质

由于要输出所有路径，所以要用深搜。又因为要非递归，所以这是一道用栈模拟深搜的题目。

难点

在我做的过程中，发现这个题目主要有这么几个难点：

1.要以链表作为栈

不能调用STL,这就需要我们自己建立栈的数据类型了 。所以这题还考差了我们对链表和栈知识 的掌握。

2.要用非递归来实现。

以前我们总是用dfs（）函数来写这种题目，然后每次调用函数结束的时候，总是会回到上次搜索的位置（比如说，按顺时针搜索，上次是搜索这个节点的上方，那当dfs（）结束时，会自动搜索右方），相当于有个记录，避免下次从头开始。而用非递归来实现，则做不到“记录上次状态”的功能。这会导致在回溯时，会走一遍和原来一模一样的路径。

3.如何将路径正序输出

由于是起点先入栈，然后依次入栈，终点最后入栈。所以，如果直接pop的话，会得到一个倒序的序列。因此，我们需要找到方法来让他正序输出。

解决方案

以链表作为栈的实现

首先，我定义了一个栈的类。

class Stack
{
    private:
    Node*top=NULL;
    int size=0;
    public:
    void Push(int row,int col);
    void Pop();
    Node*Top();
    bool Empty();
    int Size();
};

void Stack::Push(int row,int col)//节点入栈的函数
{
    Node*p=new Node;
    p->row=row;
    p->col=col;
    p->next=top;
    top=p;
    size++;
}
void Stack::Pop()//节点出栈的函数
{
    //这里注意要对空指针进行特判，不然会报错
    if(top!=NULL)
    {
        top=top->next;
    }
    size--;
}
bool Stack::Empty()//判断栈是否为空的函数
{
    //这里也要注意空指针的特判
    if(top==NULL)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}
Node* Stack::Top()//返回栈顶的指针
{
    return top;
}
int Stack::Size()//返回栈的大小
{
    return size;
}

这部分比较常规，在此就不再赘述了。唯一需要注意的是对于空指针的特判。

然后，我建立了几个栈的实例（下面会用到）

Stack pathStack;
//建立一个存储栈类型的vector，用来存储所有路径
vector<Stack> allPaths;
//存储最短的路径
Stack shortestPath;
//记录总共路径数的变量的

 非递归的实现（重点）

struct Node
{
    int row;
    int col;
    Node*next;
    //建立一个di，来记录方向，以解决非递归没办法记录上次搜索方向的问题
    int di;
};

首先，为了能记录上次这个节点搜遍了哪些方向，我建立了一个di=0.di=0,1,2,3分别代表搜过了上下左右。每次搜索让di++。

搜索算法的思路：

1.让起点入栈

2.当栈不为空的时候，循环

2.1如果到达终点，打印出路径。比较这条路径和最短路径的长度，如果更小，就覆盖最短路径。并且将终点标为未访问，回溯。

2.2如果到达终点，对这个节点向四个方向搜索。如果找到下一个可以走的节点，就把下一个节点入栈；如果没找到，回溯。

具体的搜索算法：

void Search()//核心：搜索算法
{
    //首先将起点入栈
    now_row=begin_row;
    now_col=begin_col;
    visited[begin_row][begin_col]=1;
    pathStack.Push(begin_row,begin_col);
    //当栈不为空的时候，搜索，启动！
    while(!pathStack.Empty())
    {
        //记录下现在的位置
        now_row=pathStack.Top()->row;
        now_col=pathStack.Top()->col;
        now_di=pathStack.Top()->di;
        if (now_row == end_row && now_col == end_col) //如果走到了终点
        {
            //将这条路径存进放路径的vector中
            allPaths.push_back(pathStack);
            countPaths++;
            //比较路径长短。如果更短，就把shortestPath覆盖掉
            if (shortestPath.Empty() || pathStack.Size() < shortestPath.Size()) 
            {
                shortestPath = pathStack;
            }
            //重新让终点变得可达
            visited[now_row][now_col]=0;
            //回溯到上一个节点
            pathStack.Pop();
            now_row=pathStack.Top()->row;
            now_col=pathStack.Top()->col;
            now_di=pathStack.Top()->di;
        }
        //表示是否找到下一个可达的节点
        bool found=0;
        while(now_di<4&&found==0)
        {
            now_di++;
            //对四个方向进行搜索
            switch(now_di)
            {
                case 0:
                    now_row=pathStack.Top()->row-1;
                    now_col=pathStack.Top()->col;
                    break;//向上搜索
                case 1:
                    now_row=pathStack.Top()->row;
                    now_col=pathStack.Top()->col+1;
                    break;//向右搜索
                case 2:
                    now_row=pathStack.Top()->row+1;
                    now_col=pathStack.Top()->col;
                    break;//向下搜索
                case 3:
                    now_row=pathStack.Top()->row;
                    now_col=pathStack.Top()->col-1;
                    break;//向左搜索
            }
            if(isValid(now_row,now_col))
            {
                found=1;
            }
        }
        if(found==1)//如果找到了可以走的节点
        {
            //将新的节点入栈，接着搜索
            pathStack.Top()->di=now_di;
            pathStack.Push(now_row,now_col);
            pathStack.Top()->row=now_row;
            pathStack.Top()->col=now_col;
            pathStack.Top()->di=-1;
            visited[now_row][now_col]=1;
        }
        //如果没有找到，就回溯
        else
        {
            visited[pathStack.Top()->row][pathStack.Top()->col]=0;//将这个地点标为可达 
            pathStack.Pop();//出栈
        }
    }

}

正序输出的实现

实现思路：

新建一个叫“reversedPath”的栈，然后把原栈复制过来。

之后，将原栈清空。

将“reversedPath”中的栈依次移到原栈中。

最后，将原栈输出，就得到了正序的路径。

void PrintPath(Stack &path) //打印路径
{
    memset(visited,0,sizeof(visited));
    cout<<"Step:"<<path.Size()<<endl;
    //接下来这段代码是为了将栈翻转，来输出正确的路径
    Stack reversedPath = path;//首先建立一个新的栈，将原来的栈拷贝过去
    while(!path.Empty())//然后，将原来的栈清空
    {
        path.Pop();
    }
    while (!reversedPath.Empty())//然后将翻转的栈全部出栈，并以此加入到原栈中
    {
        path.Push(reversedPath.Top()->row,reversedPath.Top()->col);
        reversedPath.Pop();
    }
    //这样我们将原栈输出，就得到了一个顺序正常的栈了！
    cout << "Path: "<<endl;
    if(path.Top()!=NULL)
    {
        cout << "(" << path.Top()->row<< ", " << path.Top()->col << ")";
        visited[path.Top()->row][path.Top()->col]=1;//这个是为了最后打印出可视化路径用的
    }
    
    path.Pop();
    while(!path.Empty())
    {
        cout << "-> (" << path.Top()->row<< ", " << path.Top()->col << ")";
        visited[path.Top()->row][path.Top()->col]=1;
        path.Pop();
    }
    cout<<endl;
    //可视化路径（用“#”来表示路）
    cout << "Visualize:('#'represents the path)"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            if(visited[i][j]==1)
            {
                cout<<"|#";
            }
            else
            {
                cout<<"|"<<map[i][j]<<"";
            }
        }
        cout<<"|"<<endl;
    }
}

其他函数的声明（可略看）

bool isValid(int next_row,int next_col)//判断走的节点是否合法
{
    if(next_row>=0&&next_row<row&&next_col>=0&&next_col<col&&map[next_row][next_col]==0&&visited[next_row][next_col]==0)
    {
        return 1;
    }
    //合法的是哪个条件：1.节点仍然在迷宫中（不越界）2.没有走到墙里面3.节点没有被访问过
    return 0;
}

上面这个函数是用来判断搜索的下一步是否合法的。额外写一个函数只是为了好看，做到“一个函数一个功能”，比较好维护。

void Initialize()
{
    memset(visited,0,sizeof(visited));
    memset(map,1,sizeof(map));
}

上面这个函数是将数组初始化的函数。同样也是为了好看。。。

void Input()//输入模块的函数
{
    //这里用英文的原因是：中文有时候会输出乱码
    cout<<"Please input the number of the row:"<<endl;
    cin>>row;
    cout<<"The maze has "<<row<<" rows."<<endl;
    cout<<"Please input the number of the column:"<<endl;
    cin>>col;
    cout<<"The maze has "<<col<<" columns."<<endl;
    cout<<"Please input the maze(from left to right,from top to down):"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            cin>>map[i][j];
        }
    }
    //这里做了一个确认的环节
    cout<<"The maze you input is:"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            cout<<"|"<<map[i][j];
        }
        cout<<"|";
        cout<<endl;
    }
    //输入起点和终点的位置
    cout<<"Please input where to start:"<<endl;
    cout<<"row:"<<endl;
    cin>>begin_row;
    cout<<"column:"<<endl;
    cin>>begin_col;
    cout<<"Please input where to end:"<<endl;
    cout<<"row:"<<endl;
    cin>>end_row;
    cout<<"column:"<<endl;
    cin>>end_col;
    cout<<"Input finish!Please wait for the result......"<<endl;
}

上面这个函数是用来输入的。因为进行了输入的确认，所以看起来比较长。

void InputTsetMap()//输入测试地图
{
    row=13;
    col=13;
    begin_row=0;
    begin_col=1;
    end_row=11;
    end_col=12;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            map[i][j]=TestMap[i][j];
        }
    }
    cout<<"The test maze is:"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            cout<<"|"<<map[i][j];
        }
        cout<<"|";
        cout<<endl;
    }
    cout<<"Input finish!Please wait for the result......"<<endl;
}

上面这个函数是用来输入初始化的迷宫的。

完整代码

#include<iostream>
#include<stdio.h>
#include<string.h>
#include <vector>
using namespace std;
struct Node
{
    int row;
    int col;
    Node*next;
    //建立一个di，来记录方向，以解决非递归没办法记录上次搜索方向的问题
    int di;
};
//建立一个栈的类（因为接下来会用到两个栈的实例，所以我就建了一个类）
class Stack
{
    private:
    Node*top=NULL;
    int size=0;
    public:
    void Push(int row,int col);
    void Pop();
    Node*Top();
    bool Empty();
    int Size();
};
int row,col,begin_row,begin_col,end_row,end_col;//这几个变量是用来存储起点和终点的坐标的
int now_row,now_col,now_di;//这几个变量是用来存储现在的坐标的
bool map[110][110];//记录迷宫
bool visited[110][110];//记录节点是否被访问过
bool TestMap[13][13]={
1,0,1,1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,1,0,0,0,0,0,1,
1,1,1,1,1,0,1,0,1,1,1,0,1,
1,0,0,0,1,0,1,0,0,0,1,0,1,
1,0,1,1,1,0,1,1,1,0,1,1,1,
1,0,0,0,1,0,0,0,1,0,0,0,1,
1,0,1,0,1,1,1,0,1,0,1,0,1,
1,0,1,0,1,0,0,0,0,0,1,0,1,
1,0,1,0,1,0,1,0,1,1,1,0,1,
1,0,1,0,0,0,1,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,1,0,1,0,1,
1,0,0,0,0,0,0,0,0,0,1,0,0,
1,1,1,1,1,1,1,1,1,1,1,1,1
};//测试地图（从老师那里来的）
Stack pathStack;
//建立一个存储栈类型的vector，用来存储所有路径
vector<Stack> allPaths;
//存储最短的路径
Stack shortestPath;
//记录总共路径数的变量的
int countPaths=0;

void Initialize()//初始化数组的函数
{
    memset(visited,0,sizeof(visited));
    memset(map,1,sizeof(map));
}
void Input()//输入模块的函数
{
    //这里用英文的原因是：中文有时候会输出乱码
    cout<<"Please input the number of the row:"<<endl;
    cin>>row;
    cout<<"The maze has "<<row<<" rows."<<endl;
    cout<<"Please input the number of the column:"<<endl;
    cin>>col;
    cout<<"The maze has "<<col<<" columns."<<endl;
    cout<<"Please input the maze(from left to right,from top to down):"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            cin>>map[i][j];
        }
    }
    //这里做了一个确认的环节
    cout<<"The maze you input is:"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            cout<<"|"<<map[i][j];
        }
        cout<<"|";
        cout<<endl;
    }
    //输入起点和终点的位置
    cout<<"Please input where to start:"<<endl;
    cout<<"row:"<<endl;
    cin>>begin_row;
    cout<<"column:"<<endl;
    cin>>begin_col;
    cout<<"Please input where to end:"<<endl;
    cout<<"row:"<<endl;
    cin>>end_row;
    cout<<"column:"<<endl;
    cin>>end_col;
    cout<<"Input finish!Please wait for the result......"<<endl;
}
void InputTsetMap()//输入测试地图
{
    row=13;
    col=13;
    begin_row=0;
    begin_col=1;
    end_row=11;
    end_col=12;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            map[i][j]=TestMap[i][j];
        }
    }
    cout<<"The test maze is:"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            cout<<"|"<<map[i][j];
        }
        cout<<"|";
        cout<<endl;
    }
    cout<<"Input finish!Please wait for the result......"<<endl;
}
void Stack::Push(int row,int col)//节点入栈的函数
{
    Node*p=new Node;
    p->row=row;
    p->col=col;
    p->next=top;
    top=p;
    size++;
}
void Stack::Pop()//节点出栈的函数
{
    //这里注意要对空指针进行特判，不然会报错
    if(top!=NULL)
    {
        top=top->next;
    }
    size--;
}
bool Stack::Empty()//判断栈是否为空的函数
{
    //这里也要注意空指针的特判
    if(top==NULL)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}
Node* Stack::Top()//返回栈顶的指针
{
    return top;
}
int Stack::Size()//返回栈的大小
{
    return size;
}
bool isValid(int next_row,int next_col)//判断走的节点是否合法
{
    if(next_row>=0&&next_row<row&&next_col>=0&&next_col<col&&map[next_row][next_col]==0&&visited[next_row][next_col]==0)
    {
        return 1;
    }
    //合法的是哪个条件：1.节点仍然在迷宫中（不越界）2.没有走到墙里面3.节点没有被访问过
    return 0;
}
void PrintPath(Stack &path) //打印路径
{
    memset(visited,0,sizeof(visited));
    cout<<"Step:"<<path.Size()<<endl;
    //接下来这段代码是为了将栈翻转，来输出正确的路径
    Stack reversedPath = path;//首先建立一个新的栈，将原来的栈拷贝过去
    while(!path.Empty())//然后，将原来的栈清空
    {
        path.Pop();
    }
    while (!reversedPath.Empty())//然后将翻转的栈全部出栈，并以此加入到原栈中
    {
        path.Push(reversedPath.Top()->row,reversedPath.Top()->col);
        reversedPath.Pop();
    }
    //这样我们将原栈输出，就得到了一个顺序正常的栈了！
    cout << "Path: "<<endl;
    if(path.Top()!=NULL)
    {
        cout << "(" << path.Top()->row<< ", " << path.Top()->col << ")";
        visited[path.Top()->row][path.Top()->col]=1;//这个是为了最后打印出可视化路径用的
    }
    
    path.Pop();
    while(!path.Empty())
    {
        cout << "-> (" << path.Top()->row<< ", " << path.Top()->col << ")";
        visited[path.Top()->row][path.Top()->col]=1;
        path.Pop();
    }
    cout<<endl;
    //可视化路径（用“#”来表示路）
    cout << "Visualize:('#'represents the path)"<<endl;
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<col;j++)
        {
            if(visited[i][j]==1)
            {
                cout<<"|#";
            }
            else
            {
                cout<<"|"<<map[i][j]<<"";
            }
        }
        cout<<"|"<<endl;
    }
}
void Search()//核心：搜索算法
{
    //首先将起点入栈
    now_row=begin_row;
    now_col=begin_col;
    visited[begin_row][begin_col]=1;
    pathStack.Push(begin_row,begin_col);
    //当栈不为空的时候，搜索，启动！
    while(!pathStack.Empty())
    {
        //记录下现在的位置
        now_row=pathStack.Top()->row;
        now_col=pathStack.Top()->col;
        now_di=pathStack.Top()->di;
        if (now_row == end_row && now_col == end_col) //如果走到了终点
        {
            //将这条路径存进放路径的vector中
            allPaths.push_back(pathStack);
            countPaths++;
            //比较路径长短。如果更短，就把shortestPath覆盖掉
            if (shortestPath.Empty() || pathStack.Size() < shortestPath.Size()) 
            {
                shortestPath = pathStack;
            }
            //重新让终点变得可达
            visited[now_row][now_col]=0;
            //回溯到上一个节点
            pathStack.Pop();
            now_row=pathStack.Top()->row;
            now_col=pathStack.Top()->col;
            now_di=pathStack.Top()->di;
        }
        //表示是否找到下一个可达的节点
        bool found=0;
        while(now_di<4&&found==0)
        {
            now_di++;
            //对四个方向进行搜索
            switch(now_di)
            {
                case 0:
                    now_row=pathStack.Top()->row-1;
                    now_col=pathStack.Top()->col;
                    break;//向上搜索
                case 1:
                    now_row=pathStack.Top()->row;
                    now_col=pathStack.Top()->col+1;
                    break;//向右搜索
                case 2:
                    now_row=pathStack.Top()->row+1;
                    now_col=pathStack.Top()->col;
                    break;//向下搜索
                case 3:
                    now_row=pathStack.Top()->row;
                    now_col=pathStack.Top()->col-1;
                    break;//向左搜索
            }
            if(isValid(now_row,now_col))
            {
                found=1;
            }
        }
        if(found==1)//如果找到了可以走的节点
        {
            //将新的节点入栈，接着搜索
            pathStack.Top()->di=now_di;
            pathStack.Push(now_row,now_col);
            pathStack.Top()->row=now_row;
            pathStack.Top()->col=now_col;
            pathStack.Top()->di=-1;
            visited[now_row][now_col]=1;
        }
        //如果没有找到，就回溯
        else
        {
            visited[pathStack.Top()->row][pathStack.Top()->col]=0;//将这个地点标为可达 
            pathStack.Pop();//出栈
        }
    }

}
int main()
{
    Initialize();
    cout<<"If you want to input your own maze,input 1."<<endl
    <<"If you want to see the test maze,input 2."<<endl;
    cout<<"Your choice:"<<endl;
    int choice;
    cin>>choice;
    if(choice==1)
    {
        Input();
        Search();
        cout<<"All paths:"<<endl;
        for(int i=0;i<countPaths;i++)
        {
            cout<<i+1<<":"<<endl;
            PrintPath(allPaths[i]);
            cout<<endl;
        }
        cout<<"The shortest path:"<<endl;
        PrintPath(shortestPath);
    }
    if(choice==2)
    {
        InputTsetMap();
        Search();
        cout<<"All paths:"<<endl;
        for(int i=0;i<countPaths;i++)
        {
            cout<<i+1<<":"<<endl;
            PrintPath(allPaths[i]);
            cout<<endl;
        }
        cout<<"The shortest path:"<<endl;
        PrintPath(shortestPath);
    }
    system("pause");
}

程序复杂度分析

空间复杂度

该程序的空间开销主要是存地图，以及存是否有被访问过。复杂度为为O（n^2）。

bool map[110][110];
bool visited[110][110];
bool TestMap[13][13]={
1,0,1,1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,1,0,0,0,0,0,1,
1,1,1,1,1,0,1,0,1,1,1,0,1,
1,0,0,0,1,0,1,0,0,0,1,0,1,
1,0,1,1,1,0,1,1,1,0,1,1,1,
1,0,0,0,1,0,0,0,1,0,0,0,1,
1,0,1,0,1,1,1,0,1,0,1,0,1,
1,0,1,0,1,0,0,0,0,0,1,0,1,
1,0,1,0,1,0,1,0,1,1,1,0,1,
1,0,1,0,0,0,1,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,1,0,1,0,1,
1,0,0,0,0,0,0,0,0,0,1,0,0,
1,1,1,1,1,1,1,1,1,1,1,1,1
};

这里我做了优化。不同于传统的int型存地图，然后用例如-1来标记访问过（开销4字节），我全部用bool型来存，另外开了个bool型的visited数组标记是否有被走过。这样节省了一半的空间开销。

此外的空间开销就是两个栈和一个vector。复杂度为O（n）。

Stack pathStack;
//建立一个存储栈类型的vector，用来存储所有路径
vector<Stack> allPaths;
//存储最短的路径
Stack shortestPath;
//记录总共路径数的变量的

时间复杂度

时间复杂度主要在于DFS。查找所有点的邻接点所需时间为O(n^2)，访问顶点的邻接点所花时间为O（1）,此时，总的时间复杂度为O(n^2)。

程序运行结果展示

我还做了一下迷宫的可视化，用“#”来表示路径。

选择自己输入迷宫

输入

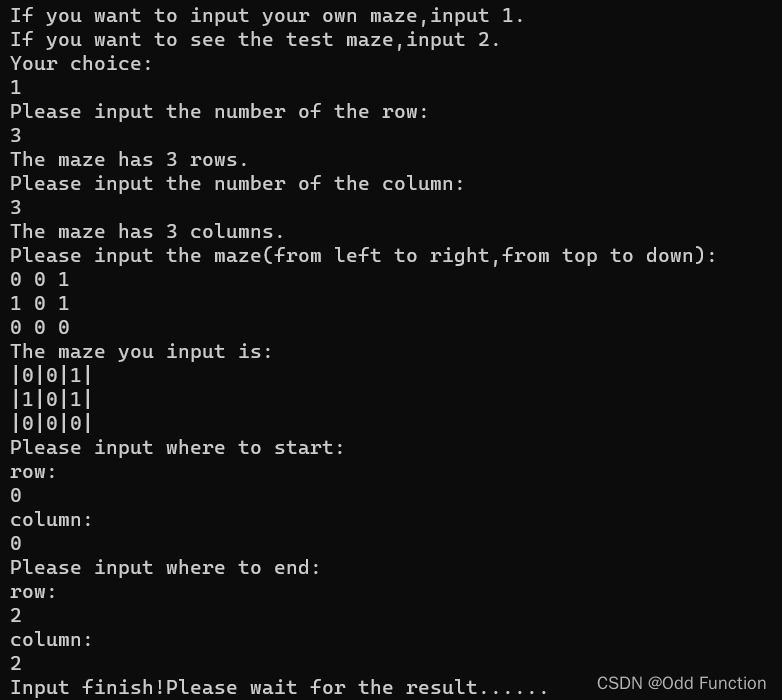
输出

选择运行测试例

输入

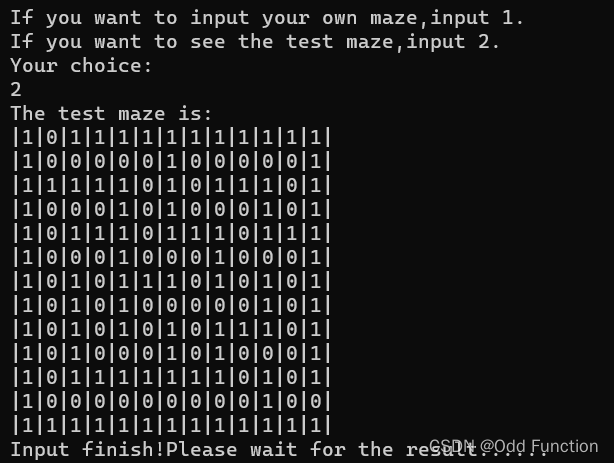
输出

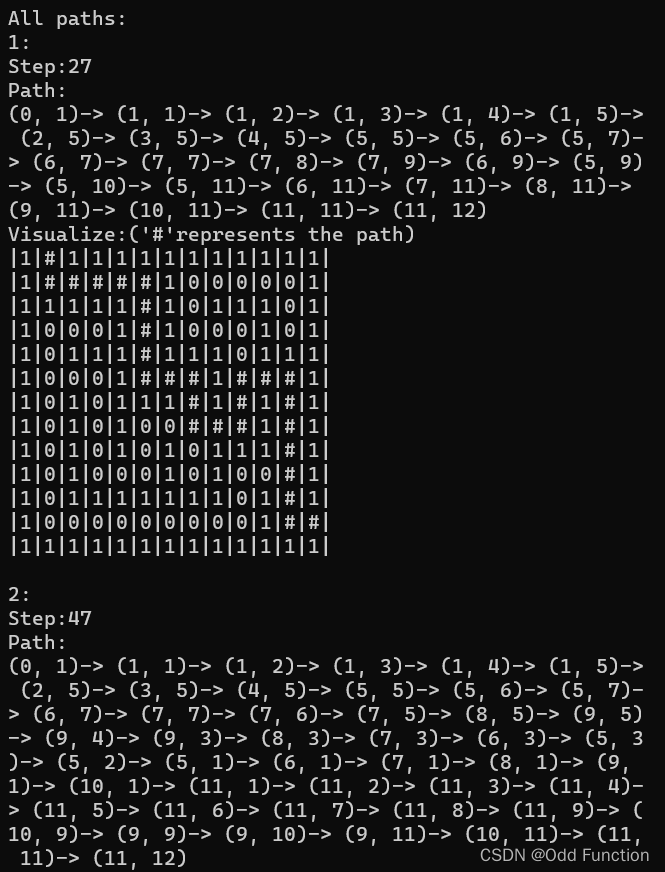
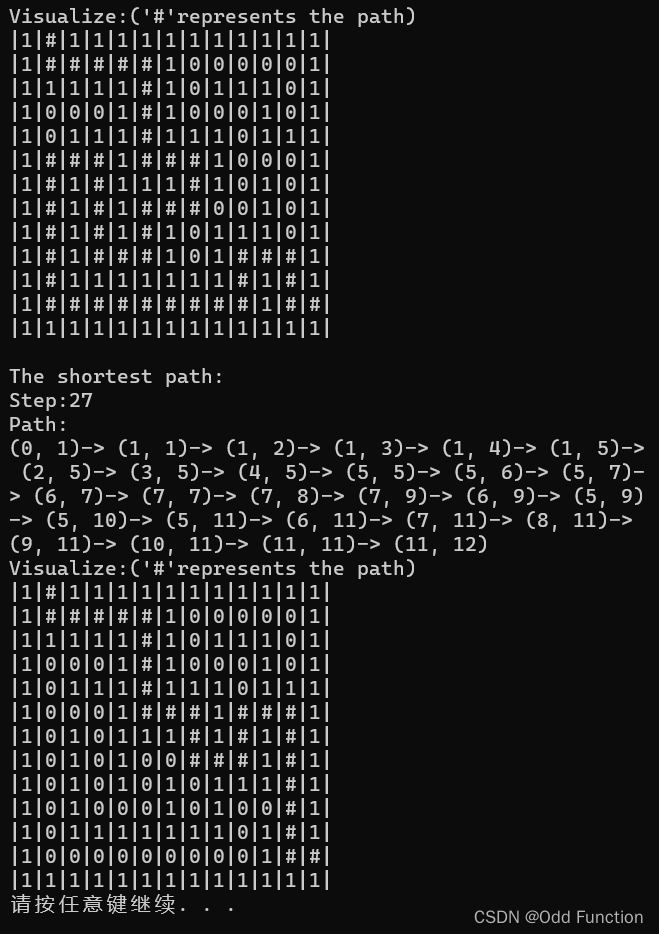
碎碎念

一开始，我只做出来了一个栈，并没有定义栈这个数据类型。

后来，由于要输出所有的路径，以及最短的路径，需要用到多个栈，我才定义了栈的数据类型。

在最后输出路径的时候，我遇到了一个问题：由于栈是先进后出的，所以如果我从上到下pop，输出来的是反向的路径。

为此，我的解决方法是：

1.再建立一个栈，叫reversedPath，并且把path赋值给它。

2.让path的元素弹出

3.将reversedPath的元素依次弹出，并且加入到新的栈中。

4.最后再把新的栈pop。

这样子，就得到了正序输出的路径。

在输出最短路径的时候，我又遇到了个问题：

如何比较路径的长短？

为了解决这个问题，我在栈这个类里面定义了一个private的元素size=0；并且开了个public的接口函数Size（）来访问这个元素。之后，我在Push函数中加了size++；，在Pop函数中加了size--。这样，不同的栈就可以通过比较size来确定最短路径了。