前言:
我们从一开始接触map和set时就惊叹于这两个容器的强大之处,set可以高效的为我们进行排序去重,而map就像一个字典一样,不仅可以为我们实现去重排序,也可以帮助我们进行一一对应的查找。接下来我们又学习了AVL树和红黑树,我们也算是了解到了map和set的底层是基于红黑树实现的。
因此现在我们已经具备对map和set进行自主实现了!在你阅读本章之前,你需要熟悉红黑树的特性,以及我们之前对list容器进行的自主实现。
从STL源码出发
我们不放先来看看STL源码中,map和set的底层是如何通过红黑树来实现的!!!
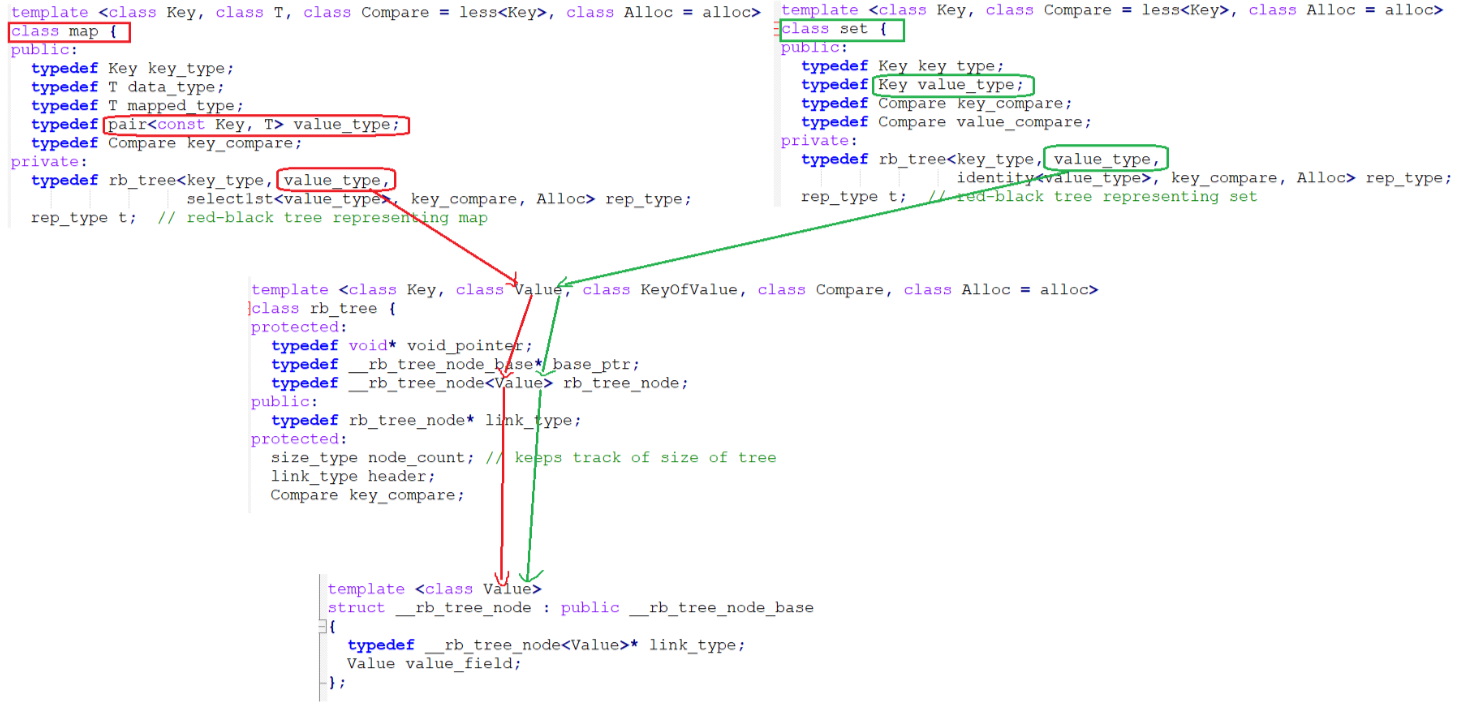
这里最重要的一点就是红黑树的第二个模版参数Value
- 对于map来说,Value是一个pair<const Key, T>类型
- 对于set来说,Value是一个Key类型
而这个Value,本质就是红黑树节点中的数据类型,简单来说,红黑树节点中存储的是一个pair还是一个K值,取决于Value!!!
为什么要这么设计?
首先,我们要知道的是,红黑树作为底层代码,它不会去关心你节点中是什么,作为创作者你只能去控制红黑树对节点数据的范围。而当我们仔细研究源码中对红黑树的模版封装时,会发现它是这么一个结构
template<class Key, class Value, class KeyOfValue, ....>
class RBTree{// ...}
既然你需要控制数据范围,这个问题很好解决,使用模版参数Value就可以很好地解决“区分两种类型”的问题。
这一点你当然可以想得到,但是为什么我还要再添加一个模版参数Key呢?而且当我们仔细剖析源码,我们会发现
- set在定义模版参数时,将Key和Value设置成了一样的
- map在定义模版参数时,给Key设置了Key_value而Value给了pair<const K, V>
很明显,对于set来说,我们会觉得class key貌似有点多余了。
对于我们后面实现的insert来说,确实是多余了
但是!我们在实现find时,你就不会这么说了。
我们先来理清find的实现逻辑
- 确定需要查找的key值
- 找到之后返回
逻辑不是问题,问题的关键在于编写find函数的返回值,对于这个返回值是个什么是最重要的。
如果红黑树只依赖 Value,那么在 map 的情况下,必须始终从 Value 中提取键,这会带来以下问题:
- 红黑树必须假设
Value一定有键存在(例如std::pair<Key, Value>的first),导致模板代码强耦合,灵活性降低。 - 如果
Value的键存储方式改变(例如改为自定义结构体),红黑树实现需要额外修改。
为什么需要在模板中记录Key的类型
排序逻辑独立于值类型:Key 作为排序依据,与 Value 分离,提升代码解耦性。
支持灵活的键提取逻辑:通过 KeyOfValue 提取键,适配 set 和 map 的不同需求。
提高效率和安全性:避免频繁提取键,优化比较性能,同时提供类型安全。
容器间复用性更高:显式记录键类型,让红黑树模板适配更多场景,而无需特化实现。
对代码进行修改处理
因为现在红黑树的各个节点即有可能是key和pair,所以我们这里直接对节点的结构体搞成一个class T即可。
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
Colour _col;
T _data;
RBTreeNode(const T& data)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)
, _data(data)
{}
};
取出节点的数据
我们在实现insert的时候,是会对红黑树的各个节点进行比较的,大的去右边、小的去左边,这一部分很好理解我就不赘述了。这里最重要的就是“从节点中取出数据”这一部分。
为什么说这一部分重要呢?
主要原因,是因为你节点里的数据类型可能是一个key,也可能是一个pair啊!你要是pair的话,那你得取出pair的first,又因为set和map是共用一颗红黑树,那你代码是写死的,而你要是用pair的fitst的话,你对于key该怎么处理呢?
所以在这里我们就可以使用仿函数来解决了,针对于map和set都应该设置一个自己的仿函数
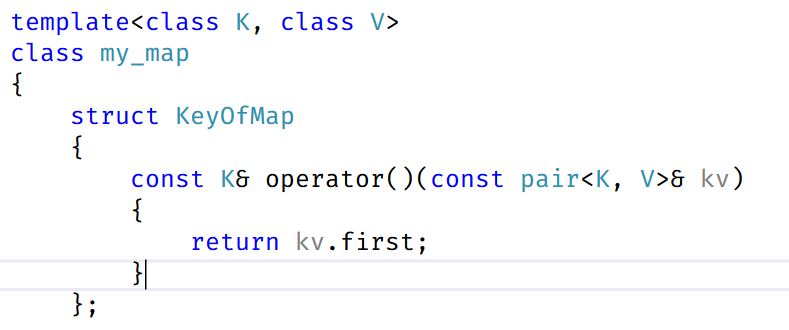
我们也要对红黑树的代码进行修改:

在insert函数中



这样不管红黑树的节点里的数据是pair还是key,我们都能将数据从中取出!!
迭代器的实现
++it
迭代器的实现也是不同于学习的vector和string,参考于我们在学习list时对迭代器的实现,在这里我们可以将迭代器封装起来,在迭代器类内部实现一个Node* _node,用来实现指向。
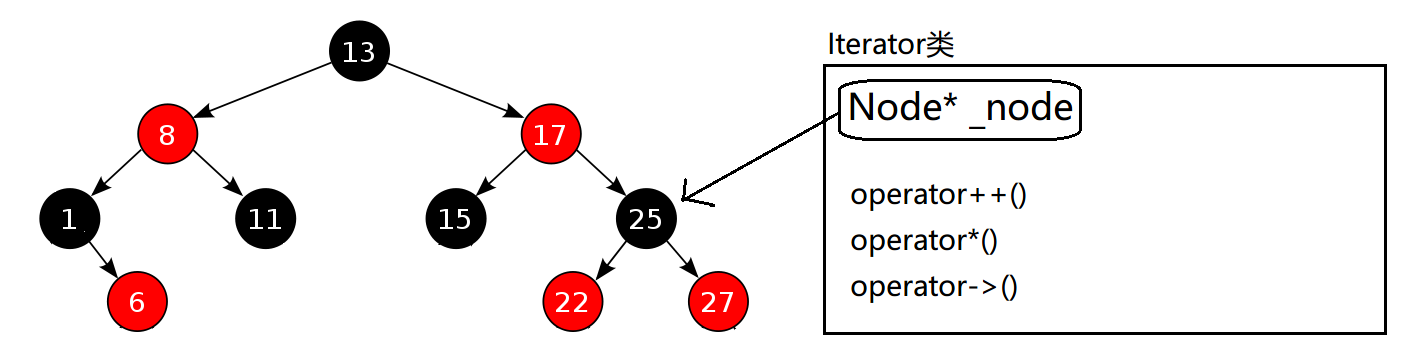
而对于++it的实现,考虑的就是类似算法的逻辑思维了
- 判断当前节点右孩子有没有数据
- 有右孩子就去找右孩子的最左节点
- 没有右孩子就去判断是要去找父亲还是找祖父
代码如下:
// 找右边的最左
Self& operator++()
{
if (_node->_right)
{
// 如果右边有数据,去右边找最左边的(找最小的)
Node* leftmin = _node->_right;
while (leftmin->_left)
{
leftmin = leftmin->_left;
}
_node = leftmin;
}
else
{
// 右边没数据了,去找父亲的父亲
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
还是很简单的。
剩下的重载及构造:
template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, Ref, Ptr> Self;
// 精华所在
Node* _node;
__RBTreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const Self& s)
{
return _node != s._node;
}
};
实现operator[]
我们在讲解map的时候,提到过map拥有自己的[],这是个很实用高效的功能,所以我们不妨来自己手搓一个。
最主要的问题就是insert插入的时候,是返回的pair<iterator, bool>。
所以我们还要进行修改。
V& operator[](const K& key)
{
pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));
}
// 为了实现map的方括号重载,所以这里需要进行修改
pair<Iterator, bool> Insert(const T& data)
{
// 实例化仿函数
KeyOfT kot;
// 判断“根节点”是否为空
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(Iterator(_root), true);
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kot(data) < kot(cur->_data))
{
// 小的去左边
parent = cur;
cur = cur->_left;
}
else if (kot(data) > kot(cur->_data))
{
// 大的去右边
parent = cur;
cur = cur->_right;
}
else return make_pair(Iterator(cur), false);
}
cur = new Node(data);
cur->_col = RED; // 默认新增节点给红色
if (kot(cur->_data) < kot(parent->_data)) parent->_left = cur;
else parent->_right = cur;
cur->_parent = parent;
// parent的颜色是黑色也结束
while (parent && parent->_col == RED)
{
Node* grandparent = parent->_parent;
if (parent == grandparent->_left)
{
Node* uncle = grandparent->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandparent->_col = RED;
// 继续向上更新
cur = grandparent;
parent = cur->_parent;
}
else
{
// 叔叔不存在,或者为黑
if (cur == parent->_left)
{
// g
// p u
// c
RotateR(grandparent);
parent->_col = BLACK;
grandparent->_col = RED;
}
else
{
// g
// p u
// c
RotateL(parent);
RotateR(grandparent);
cur->_col = BLACK;
grandparent->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandparent->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandparent->_col = RED;
// 继续向上更新
cur = grandparent;
parent = cur->_parent;
}
else
{
// 叔叔不存在,或者为黑
if (cur == parent->_right)
{
// g
// u p
// c
RotateL(grandparent);
parent->_col = BLACK;
grandparent->_col = RED;
}
else
{
// g
// u p
// c
RotateR(parent);
RotateL(grandparent);
cur->_col = BLACK;
grandparent->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(Iterator(cur), false);
}
void InOrder()
{
return _InOrder(_root);
cout << "\n";
}
bool IsBanlance()
{
if (_root->_col == RED)
{
return false;
}
int refNum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refNum;
}
cur = cur->_left;
}
return _IsValidRBTRee(_root, 0, refNum);
}
总结:
以上就是map和set的主要逻辑结构,简单总结一下,我们在下来自主实现的时候,在处理仿函数还有理解源码时会出现困难,但是对于迭代器的实现这部分逻辑,我觉得目前阶段我们简单讲解不成问题,如果你对迭代器的封装存在疑问,不妨去看看我之前写的对list的迭代器进行封装那部分再回顾回顾。https://blog.youkuaiyun.com/weixin_72917087/article/details/137979785?spm=1001.2014.3001.5502
全部代码在我的gitee下:https://gitee.com/wushuangqq/c_-plus_-plus_-acer/tree/master/my_map&&set/my_map&&set




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










