public class exemple {
public static void findPrimePlan1(int n){
//埃氏筛
List<Integer> prime = new ArrayList<>();//存储素数
boolean[] isPrime = new boolean[n + 1];//0 - 100的下标,开始所有都为素数假设
for(int i = 2;i <= n;i++){
if(!isPrime[i]){//加入素数
prime.add(i);
if((long) i * i > n){
continue;
}
for (int j = i * i; j <= n; j += i) {//删除为合数
isPrime[j] = true;
}
}
}
for(int x : prime){
System.out.print(x + " ");
}
}
public static void findPrimePlan2(int n) {
//线性筛
List<Integer> prime = new ArrayList<>();//存储素数
boolean[] isPrime = new boolean[n + 1];//0 - 100的下标,开始所有都为合数假设
for (int i = 2; i <= n; i++) {
if(!isPrime[i]){
prime.add(i);
}
for(int x : prime){
if(x * i > n){
break;
}
isPrime[x * i] = true;
if(i % x == 0){
break;
}
}
}
for(int x : prime){
System.out.print(x + " ");
}
}
public static void main(String[] args) {
long start1 = System.currentTimeMillis();
findPrimePlan1(100000000);
long end1 = System.currentTimeMillis();
System.out.println();
System.out.println(end1 - start1);
long start2 = System.currentTimeMillis();
findPrimePlan2(100000000);
long end2 = System.currentTimeMillis();
System.out.println();
System.out.println(end2 - start2);
}
}
先将最终代码放在这里
1.埃氏筛
埃氏筛是先将比如你找出0 - 100 之间的素数,我们先建立一个boolean类型的数组,以下标当作0 - 100 的数字,先将所有的数都当作素数标记为false,当遇到合数标记成素数
其中标记的方法是素数相乘就是合数
比如2是素数,2 * i 和 3 * i 等等都属于合数我们都标记成true
所以每一次我们将素数先添加到我们准备好的素数存储数组之中,然后将属于合数的全部进行标记
划掉合数的例子

细节
public static void findPrimePlan1(int n){
//埃氏筛
List<Integer> prime = new ArrayList<>();//存储素数
boolean[] isPrime = new boolean[n + 1];//0 - 100的下标,开始所有都为素数假设
for(int i = 2;i <= n;i++){
if(!isPrime[i]){//加入素数
prime.add(i);
if((long) i * i > n){//细节1
continue;
}
for (int j = i * i; j <= n; j += i) {//细节2
isPrime[j] = true;
}
}
}
for(int x : prime){
System.out.print(x + " ");
}
}1 ) 我在写代码过程中发现如果没有注意到细节1的话,当你输入的n为1000000就会发生溢出
原因就在i * i上,我们使用的是int来存储相乘就会发生溢出的情况,所以我们要加上细节1来进行判断
将 i 强转成long相乘来判断是否大于n,如果大于n的话就不需要进行划掉合数直接跳到下一个数进行
2) 我开始是填 i * 2来作为j的开始,发现这样会影响效率会出现多次划掉同一个元素(不加其实也会,加了会快一内内),然后改成了i * i
(3) 由于我设立的数组是0 - 100我是判断包含100的元素,所有要注意<=号的添加,如果不添加的话会漏掉100这个元素
2.欧拉筛
欧拉筛对埃氏筛进行了一定的优化,不会发生重复的划掉同一个合数,如埃氏筛举例中划掉相同元素会浪费时间
public static void findPrimePlan2(int n) {
//线性筛
List<Integer> prime = new ArrayList<>();//存储素数
boolean[] isPrime = new boolean[n + 1];//0 - 100的下标,开始所有都为合数假设
for (int i = 2; i <= n; i++) {
if(!isPrime[i]){
prime.add(i);
}
for(int x : prime){
if(x * i > n){
break;
}
isPrime[x * i] = true;
if(i % x == 0){
break;
}
}
}
for(int x : prime){
System.out.print(x + " ");
}
}由于每个数都有一个最小的质因子,我们根据每个数最小的质因子来划掉合数
划掉合数的例子
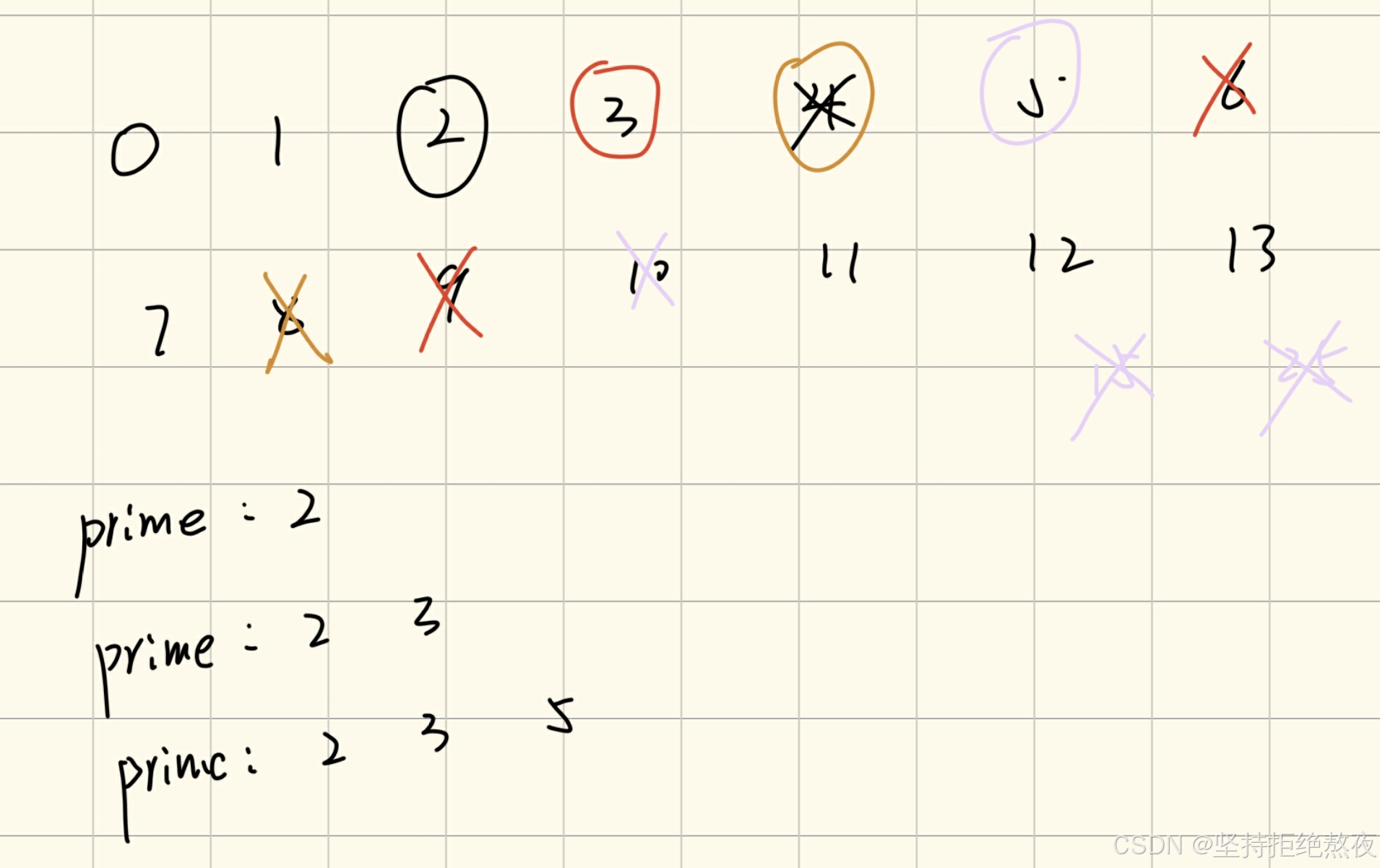
欧拉筛是将每一个标记为素数的元素先添加到prime里面,然后将prime里的元素进行逐一判断,如果相乘大于n就直接退出循环,没有大于就将合数划掉,然后判断是不是最小的质因子
比如4的最小质因子是2所以划掉8之后就会停止(自己模拟一遍比较好)
细节
欧拉筛唯一需要注意的就是 <= 符号,如果你不包括100的话就不需要=号























 783
783

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








