刷题计划 day21 二叉树（十）【删除二叉搜索树中的节点】【修剪二叉搜索树】【将有序数组转换为二叉搜索树】【把二叉搜索树转换为累加树】

⚡刷题计划day21 二叉树（十）继续，二叉树专题终于结束了哈哈，下一期是回溯专题，敬请期待关注，可以点个免费的赞哦~

往期可看专栏，关注不迷路，

您的支持是我的最大动力🌹~

目录

题目一：50. 删除二叉搜索树中的节点

题目二：669. 修剪二叉搜索树

题目三：108. 将有序数组转换为二叉搜索树

题目四：538. 把二叉搜索树转换为累加树

---

题目一：50. 删除二叉搜索树中的节点

50.删除二叉搜索树中的节点

(https://leetcode.cn/problems/delete-node-in-a-bst/description/)

删除会比插入要复杂一些，需要考虑的情况比较多。

---

有以下五种情况：

• 第一种情况：没找到删除的节点，遍历到空节点直接返回了

• 找到删除的节点

  • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点

  • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点

  • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点

  • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

第五种情况有点难以理解，看下面动画：

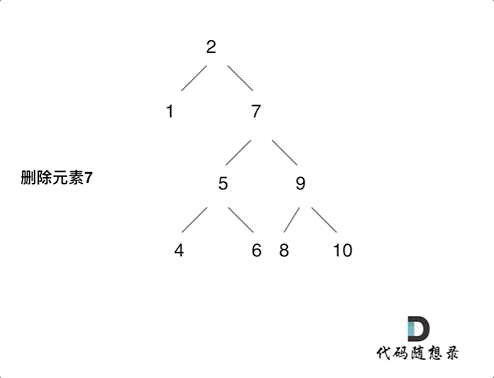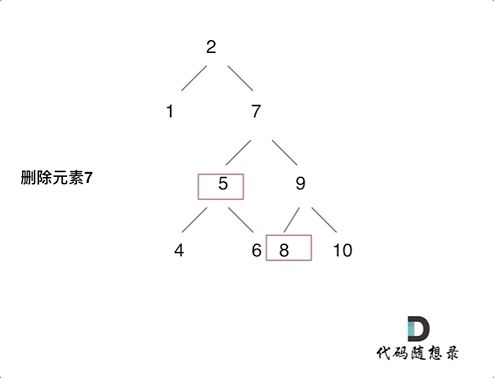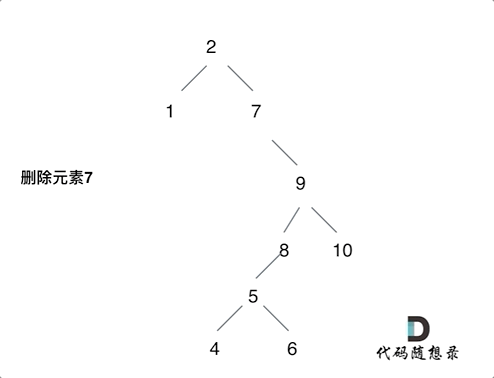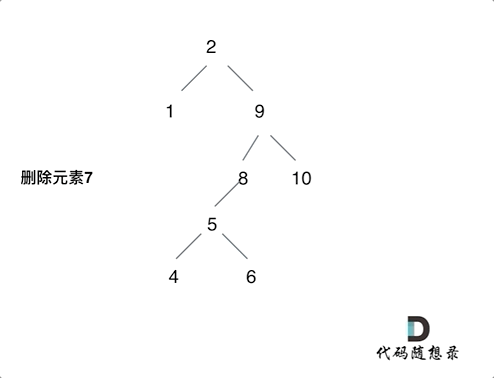
AC代码如下：

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
​
        if (root ==null){
            return root;
        }
​
        if(key==root.val){
​
            if(root.left==null && root.right==null) {
                return null;
            }else if (root.left==null) {
                return root.right;
            }else if (root.right==null) {
                return root.left;
            }else {
                TreeNode cur = root.right;
                while (cur.left!=null){
                    cur = cur.left;
                }
                cur.left = root.left;
                root = root.right;
                return root;
            }
        }
        if(key<root.val) root.left = deleteNode(root.left,key);
        if(key>root.val) root.right = deleteNode(root.right,key);
        return root;
    }
}

题目二：669. 修剪二叉搜索树

669.修剪二叉搜索树

(https://leetcode.cn/problems/trim-a-binary-search-tree/description/)

主要思路：

• 若 root.val 小于边界值 low，则 root 的左子树必然均小于边界值，我们递归处理 root.right 即可；

• 若 root.val 大于边界值 high，则 root 的右子树必然均大于边界值，我们递归处理 root.left 即可；

• 若 root.val 符合要求，则 root 可被保留，递归处理其左右节点并重新赋值即可

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) return null;
        if (root.val < low) return trimBST(root.right, low, high);
        else if (root.val > high) return trimBST(root.left, low, high);
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}
参考题解

题目三：108. 将有序数组转换为二叉搜索树

108.将有序数组转换为二叉搜索树

(https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/)

题目需要我们将有序数组转换为一棵平衡二叉搜索树。

那怎么处理呢？因为是有序数组，我们直接取Mid节点即可。

那么如果数组长度为偶数，中间节点有两个取那个呢？都是可以的，只是构成了不同的平衡二叉搜索树。

例如：输入：[-10,-3,0,5,9]

如下两棵树，都是这个数组的平衡二叉搜索树：

然后就简单了，我们之前也做过构造二叉树的方法，不多叙述，直接看代码更加清晰：

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        TreeNode root = dfs(nums,0,nums.length-1);//左闭右闭
        return root;
​
    }
​
    public TreeNode dfs(int[] nums,int left,int right){
        if(left>right){
            return null;
        }
​
        int mid = left + ((right-left)>>1);
        TreeNode root = new TreeNode(nums[mid]);
        root.left = dfs(nums,left,mid-1);
        root.right = dfs(nums,mid+1,right);
        return root;
    }
}

题目四：538. 把二叉搜索树转换为累加树

58.把二叉搜索树转换为累加树

(https://leetcode.cn/problems/convert-bst-to-greater-tree/description/)

一看到累加树，相信很多小伙伴都会疑惑：如何累加？遇到一个节点，然后再遍历其他节点累加？怎么一想这么麻烦呢。

然后再发现这是一棵二叉搜索树，二叉搜索树啊，这是有序的啊。

那么有序的元素如何求累加呢？

其实这就是一棵树，大家可能看起来有点别扭，换一个角度来看，这就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]，是不是感觉这就简单了。

怎么遍历呢，我们从后向前累加就OK了。

从树中遍历顺序则是右中左，然后累加即可。

思路明白了，那具体代码怎么实现呢，

见代码即可：

class Solution {
    int sum =0;
    public TreeNode convertBST(TreeNode root) {
    dfs(root);
    return root;
​
    }
    public void dfs(TreeNode root){
        if(root==null){
            return;
        }
        dfs(root.right);
        sum += root.val;
        root.val = sum;
        dfs(root.left);
    }
}

点个免费的赞赞吧~