卷积的原理

一、卷积的概念

卷积（Convolution）是一种积分变换的数学方法，常用在数字信号处理、通信系统或者光学系统中。而在人工神经网络中，卷积操作是一种特殊的线性变换，它的设计灵感来自于生物学中的视觉系统，旨在模拟人类视觉处理的方式。

人工神经网络中的卷积过程为：使用卷积核（即滤波器）在输入数据上进行滑动，每次计算与卷积核重叠部分的点乘和。 这样的操作可以提取输入数据的局部特征，实现特征的共享和抽象，从而使得网络对输入数据的变化更加鲁棒和准确。

卷积核，是一种可学习的滤波器，用于对输入图像进行特征提取。卷积核通常是一个小的二维矩阵，其大小通常为 k×k ，其中 k 是一个正整数，称为卷积核大小（例如3*3, 5*5, 7*7等等），卷积核的大小也可以称为感受野。

二、卷积的操作

卷积核的值通常是由神经网络自动学习得到的。卷积核的作用是提取输入数据的局部特征。在卷积操作中，卷积核可以识别输入图像中的不同特征，例如边缘、纹理、角落等，从而提取更加高级的特征表示。

最常见的二维卷积操作，由一个二维输入数组和一个二维卷积核数组通过卷积运算，输出一个二维数组，例如下图所示：

通常，卷积层的操作是由多个输入和多个卷积核分别进行运算，然后再求和，以提取更为抽象的特征，比如下图：

上图中，通过2个输入通道和2个卷积核可以求出一组特征，那么，通过多个卷积核，就可以生成多个输出层（即提取多个抽象的特征）。比如2个通道和4个卷积核，就可以卷积出两组特征。

以下为3个通道和6个卷积核，输出两组特征的示例：

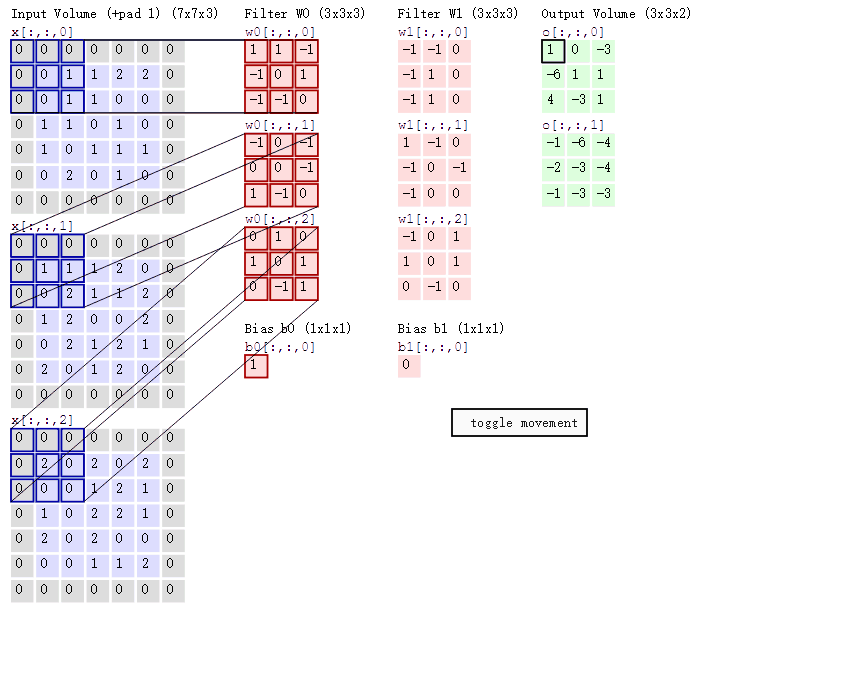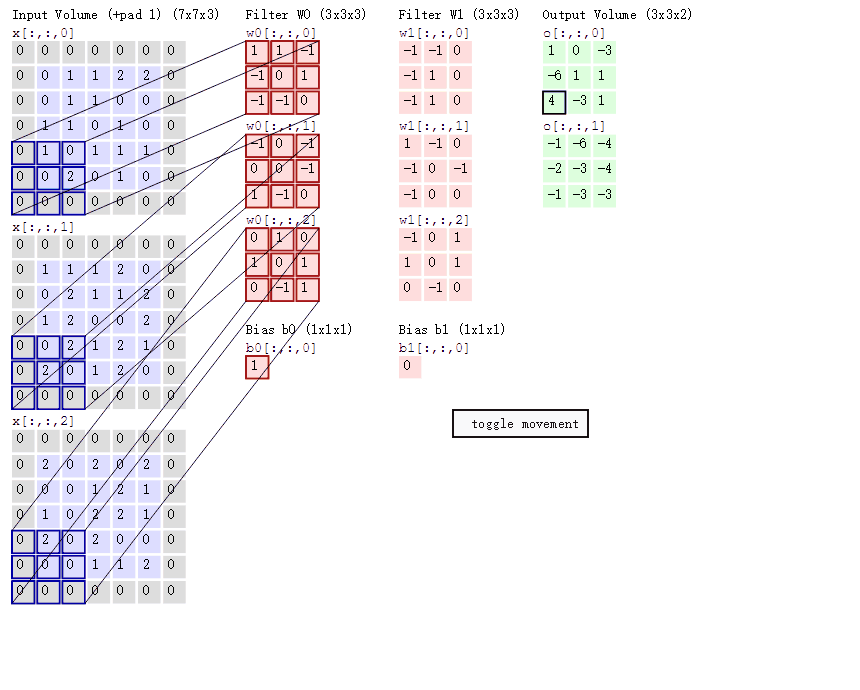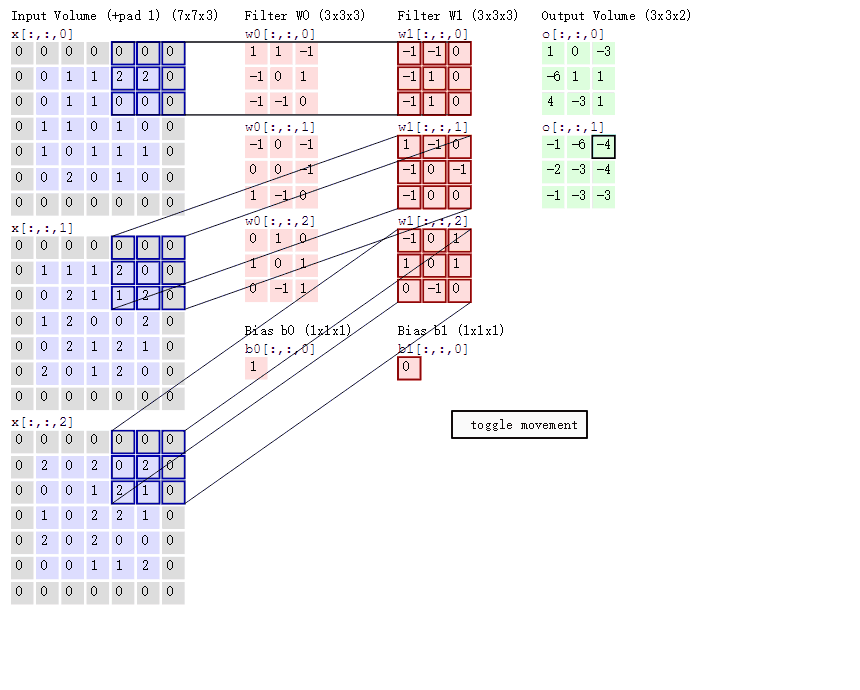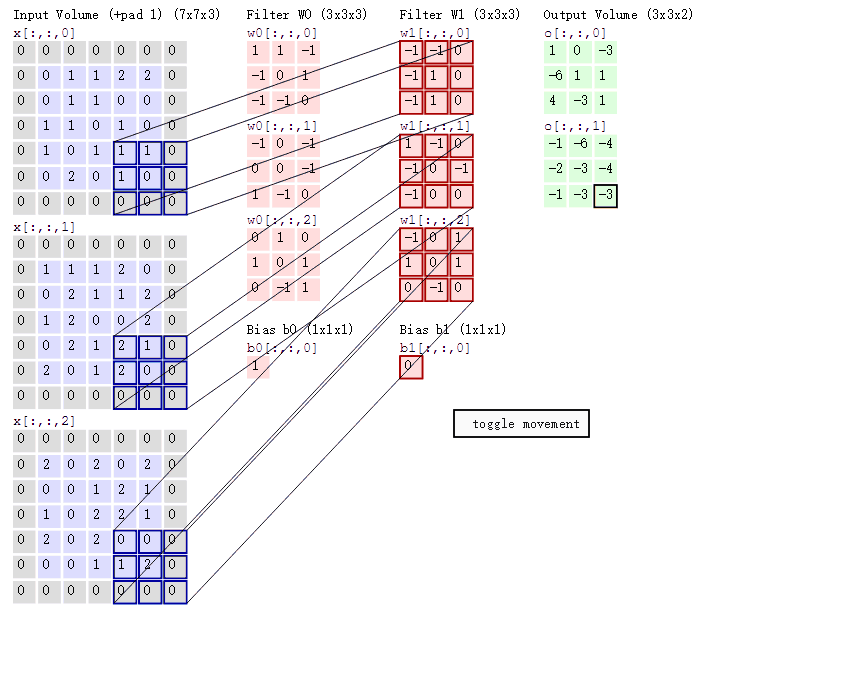
上图中，我们可以看到最左边的矩阵周围都是0，就是做了填充的操作。

例如：输入图像大小为3*3，卷积核大小为2*2，卷积的步长为1，那么输出的矩阵大小为2*2。可以看出，输出的大小比输入大小减小了。

为了操持输入大小与输出大小一致，则需要在输入的高和宽两侧填充元素（通常使用0进行填充）。

下图可以更直观的看到卷积的过程：

三、图像卷积后的可视图：

通过不同的卷积核，可以看到图像的不同特征，如下图所示：

因此，多个卷积核，就可以提取图像的丰富的特征。

参考来源：

【深度学习】一文搞懂卷积神经网络（CNN）的原理（超详细）_卷积神经网络原理-优快云博客

更多：

⁣西克中国 | SICK

传感器技术学习平台