红黑树插入过程

红黑树特点

1. 一个节点要么是黑色，要么是红色；
2. 根节点是黑色；
3. 所有叶子节点是黑色的，而且叶子节点不存储数据；
4. 红色节点的左右孩子节点都是黑色；
5. 从根节点到叶子节点通过的黑色节点个数相同；

红黑树节点插入过程

新节点默认为红色

插入的新的节点颜色都是红色。

根节点固定为黑色

如果新插入的节点是红黑树的根节点，那么应该变为黑色。

父节点为黑色，直接插入

父节点为红色

叔节点为红色

将父节点和叔节点变为黑色，同时将爷爷节点变为红色，以爷爷节点为当前节点，继续判断。

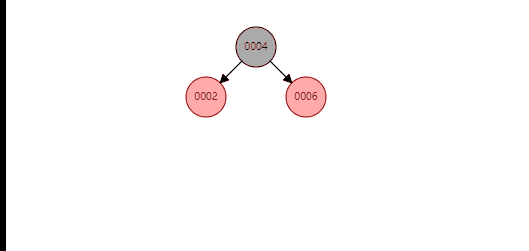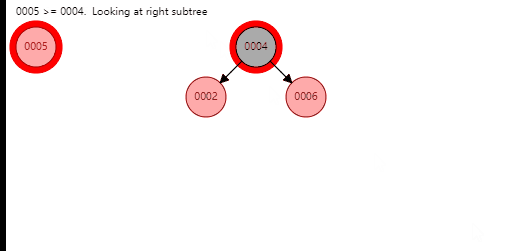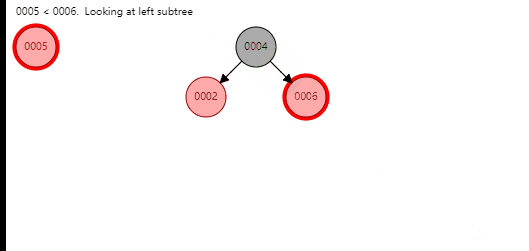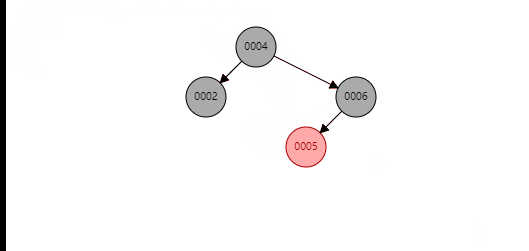
叔节点为黑色（空节点）

这种情况会稍微麻烦点，具体还要分为两种情况，

1. 父节点为爷爷节点的左孩子节点而且新节点为父节点的右孩子节点，或父节点为爷爷节点的右孩子节点而且新节点为父节点的左孩子节点；
2. 父节点为爷爷节点的左孩子节点而且新节点为父节点的左孩子节点，或父节点为爷爷节点的右孩子节点而且新节点为父节点的右孩子节点。

情况1

对于第一种情况，需要首先进行旋转，变成新节点是爷爷节点的左孩子，父节点是新节点的左孩子；或新节点是爷爷节点的右孩子，父节点是新节点的右孩子，针对第一种情况，看图

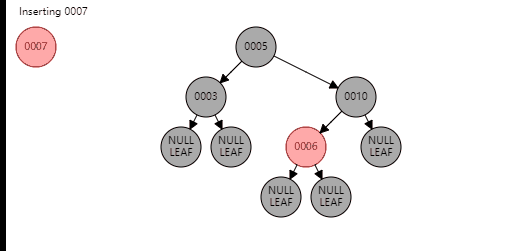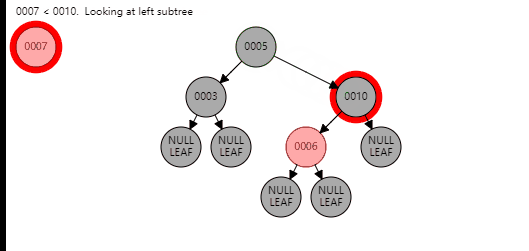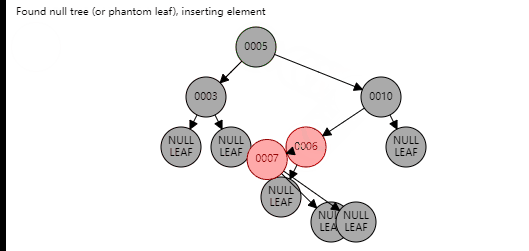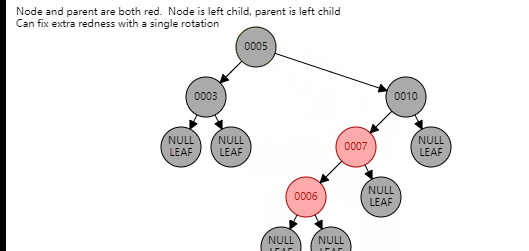
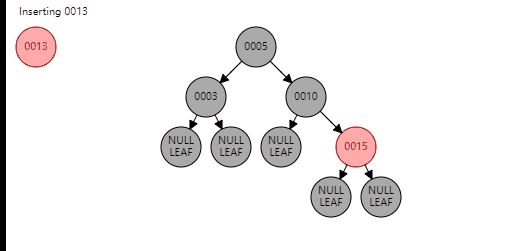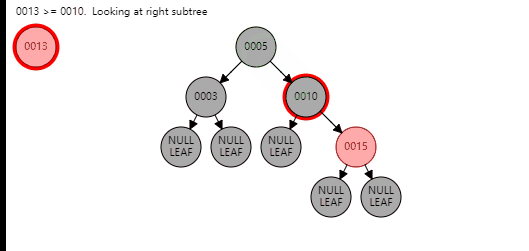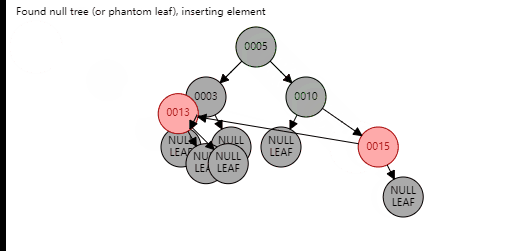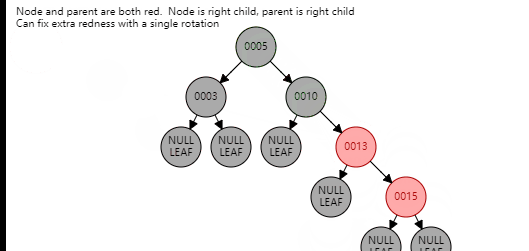
到这里，第一种情况都变成了第二种情况，新节点和父节点和爷爷节点在一条线上，下面按照第二种情况进行操作即可。

情况2

这里就是比较简单的旋转了，主要分为两步，旋转、变色，直接看图就可以

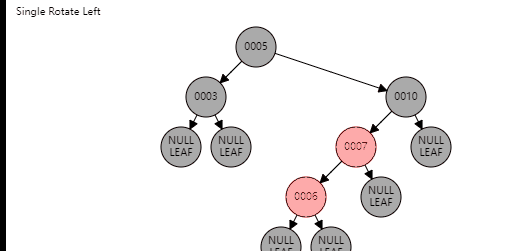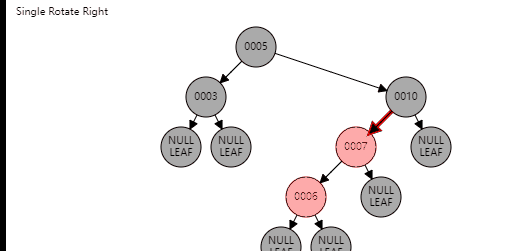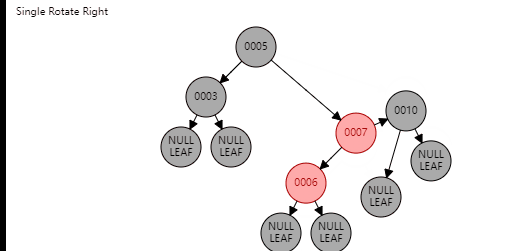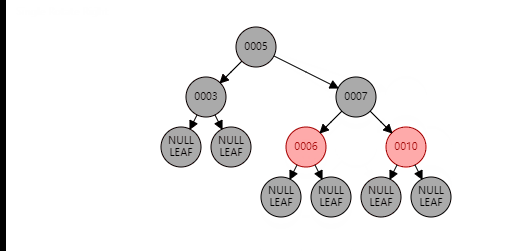
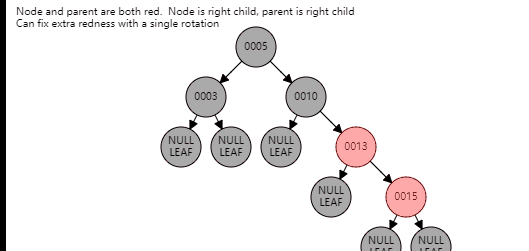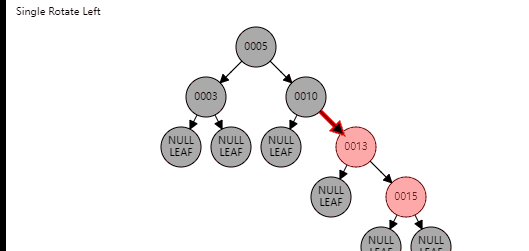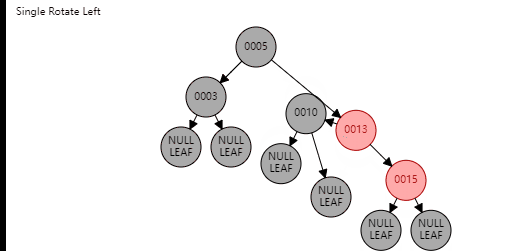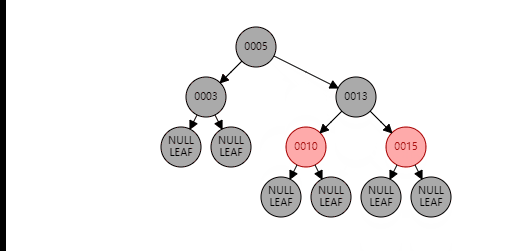
叔节点为黑色（非空）

这种情况只会出现在从叶节点向根节点调整的过程中，看图（例子中按照顺序插入1 3 5 7 9 11 13后暂停，再插入15即可）

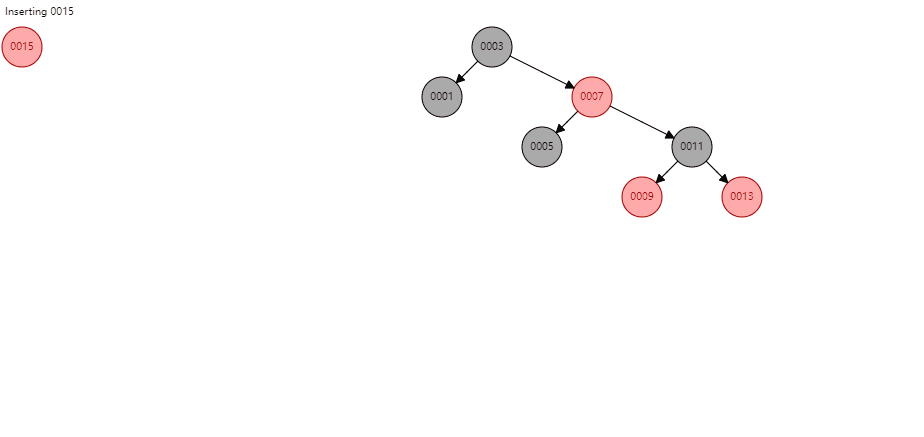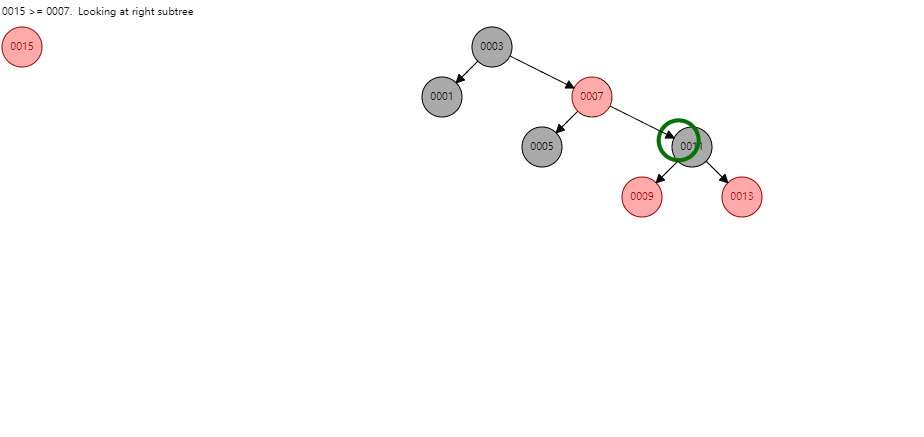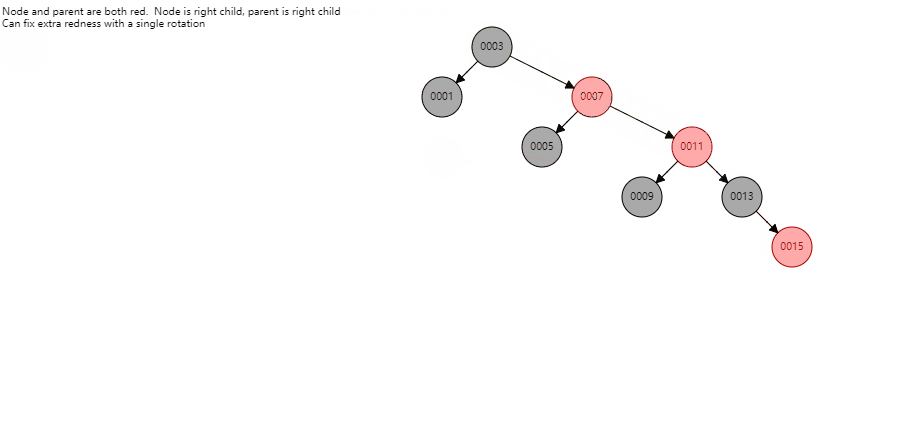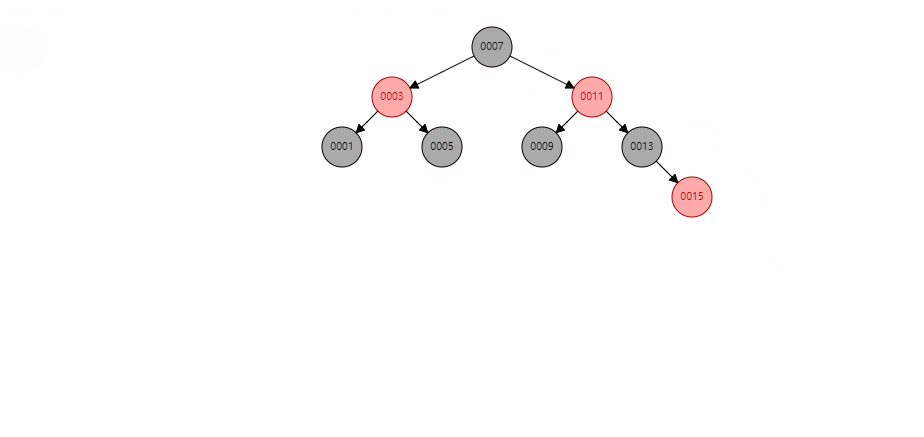
在对新节点15的父辈节点和爷爷节点调整颜色后，以新节点15的爷爷节点11为当前节点，发现11的父节点为红且叔节点为黑且叔节点不是空，调整过程为：

1. 将11节点的父节点往上提；
2. 将11的爷爷节点3作为父节点7的左孩子节点，同时将父节点7的左孩子节点作为爷爷节点3的右孩子节点；
3. 旋转后，将11的父节点7和11的兄弟节点对换颜色即可。

可以自己生成些随机数，通过下方可视化网站看下具体过程。

---

完…

https://www.cs.usfca.edu/~galles/visualization/Algorithms.html