Python| 水文 |利用动态规划求解水电站机组间最优负荷分配问题（附代码）

本文链接：https://blog.youkuaiyun.com/weixin_67437706/article/details/143101606

Tips：
本期向大家分享水电站厂内经济运行中求解机组间最优负荷分配的代码编写，其主要思路还是动态规划（之前有发过一期用动态规划做优化调度的博客），我们仍然是结合具体例题，用代码去实现它。

1 算例说明

选用教材《水利水电工程优化调度》（唐德善唐彦黄显峰史记毅超等编著）（中国水利水电出版社）上对应P56页的例题进行代码验证。

1.1具体例题资料

1.2思路说明

我们需要关注的信息是：
1）共有4台机组（i=1，2，3，4），其中3台小机组最大负荷为3万kw，1台大机组（i=2）最大负荷为4万kw；

2）表4-1中，i对应的行表示各机组；N对应的列表示各机组可能的负荷；

3）表4-1中，表格内具体的值表示流量Q，即：该机组在该负荷下的发电流量；

4）我们的目的是求：在总负荷为NCT=5kw时，满足该负荷要求且总的发电流量最小的方案；

5）把方案用[ ]储存，比如[0，1，0，1，0]表示N2机组和N4机组各负荷1万kw，总出力2万kw。

2 代码内容

注：以下所有代码均按顺序在同一个py文件里，方便解释才将其拆开

2.1参数设置

按照题意和表4-1数据将参数进行设置。最大总负荷为5kw，4个机组最大负荷分别为3kw，4kw，3kw，3kw，与之对应的有4个流量列表，针对各机组相应负荷会有对应的流量。

import numpy as np
# H1=35 #水头m（此例题用不上）
NCT=5 #最大总负荷kw
# 第一台机组对应装机容量
P1=3
# 第二台机组对应装机容量
P2=4
# ... ...
P3=3
P4=3

# 第一台机组对应负荷的发电流量
Q11=[0,30,34,38] #水流m3/s
# 第二台机组对应负荷的发电流量
Q12=[0,31,34,37,40]
# ... ...
Q13=[0,29,35,38]
Q14=[0,28,35,37]

2.2 数据整理

为了后续方便调用和索引，首先将各机组的可能出力用列表推导式生成列表进行储存，然后将数据以二维表的形式储存在数组中，我叫它tab。表格的第一列表示该机组可能出力，第二列表示对应的发电流量，而后定义为函数get_tab，通过接收参数N，Q：对应机组的可能出力以及发电流量列表，返回二维表。本题有4个机组，所以调用函数后会生成4个tab。

# 生成各机组对应可能的出力
N1=[i for i in range(0,P1+1)]
N2=[i for i in range(0,P2+1)]
N3=[i for i in range(0,P3+1)]
N4=[i for i in range(0,P4+1)]
# 获取二维表格：出力N对应的流量Q
def get_tab(N,Q):
    tab=np.zeros((len(N),2))
    for i in range (len(N)):
        n=N[i]
        q=Q[i]
        tab[i,0]=n
        tab[i,1]=q
    return tab
tab1=get_tab(N1,Q11)
tab2=get_tab(N2,Q12)
tab3=get_tab(N3,Q13)
tab4=get_tab(N4,Q14)

2.3最优负荷分配计算

将整个规划分配过程定义为函数plan，通过接收参数NCT（最大总负荷），返回最终所有可能总负荷对应的最优方案。k对应的for循环用于遍历可能总负荷（1万kw，2万kw，3万kw，4万kw，5万kw），i、j、a、b对应的for循环用于遍历4个机组各自的可能出力，当满足4个机组的组合出力加起来等于总负荷时，则将对应的出力值在tab中进行索引，找到其所在行，该行第1个元素是出力N，第2个元素是发电流量Q。而后通过获取tab中对应的流量值并相加，求得该方案下的总流量。在求得的上述方案中选择各可能总负荷对应的最优负荷分配方案进行保留储存。判断各可能总负荷是否对应了多个最优方案，将多个方案存储到同一个子列表里。最后添加表头文字便于识别各元素含义。

def plan(NCT):
    lst_Nr=[i for i in range(0,NCT+1)]
    lst_PLAN=[]
    for k in(lst_Nr):
        lst_save = []
        lst_q=[]
        lst_plan = [k]
        for i in(N1):
            for j in(N2):
                 for a in(N3):
                     for b in(N4):
                         if i+j+a+b==k:
                             q1_index=np.where(tab1[:,0] == i)[0]
                             q2_index=np.where(tab2[:,0] == j)[0]
                             q3_index=np.where(tab3[:,0] == a)[0]
                             q4_index=np.where(tab4[:,0] == b)[0]
                             q=tab1[q1_index.item()][1]+tab2[q2_index.item()][1]+tab3[q3_index.item()][1]+tab4[q4_index.item()][1]
                             lst_q.append(q)
                             a_forindex=[i,j,a,b,q]
                             lst_save.append(a_forindex)
        # 列表转换为数组方便找索引
        a_save=np.array(lst_save)
        # 找到流量最小的行索引
        min_row=np.where(a_save[:,4]==min(lst_q))[0]
        # 如果符合if，说明有多个相同的最小值
        if len(min_row)>1:
            # item()用来提取数组的值作为最后的索引
            for i in range(len(min_row)):
                # 将多个方案追加到lst_plan中，比如：k=2时，有两个方案的q最小
                # 都是34，对应lst_save[min_row[i]]的值为[2,0,34]和[0,2,34]
                # 追加之后，首个元素是k=2，代表了当前要求出力N，便有：[2,[2,0,34],[0,2,34]]
                lst_plan.append(lst_save[min_row[i]])
        # 如果只有一个最小值，直接item提取值，索引到相应方案，追加到lst_plan中
        else:
            lst_plan.append(lst_save[min_row.item()])
        lst_PLAN.append(lst_plan)
    lst_PLAN.insert(0, ['N', 'N1', 'N2', 'N3', 'N4', 'Q'])
    return lst_PLAN

2.4 结果输出

调用plan函数，获取最优方案。由于最优方案是以嵌套列表的形式存储的，所以遍历result，输出子列表。

result=plan(NCT)
# 遍历嵌套列表，每行输出一个子列表
for sublist in result:
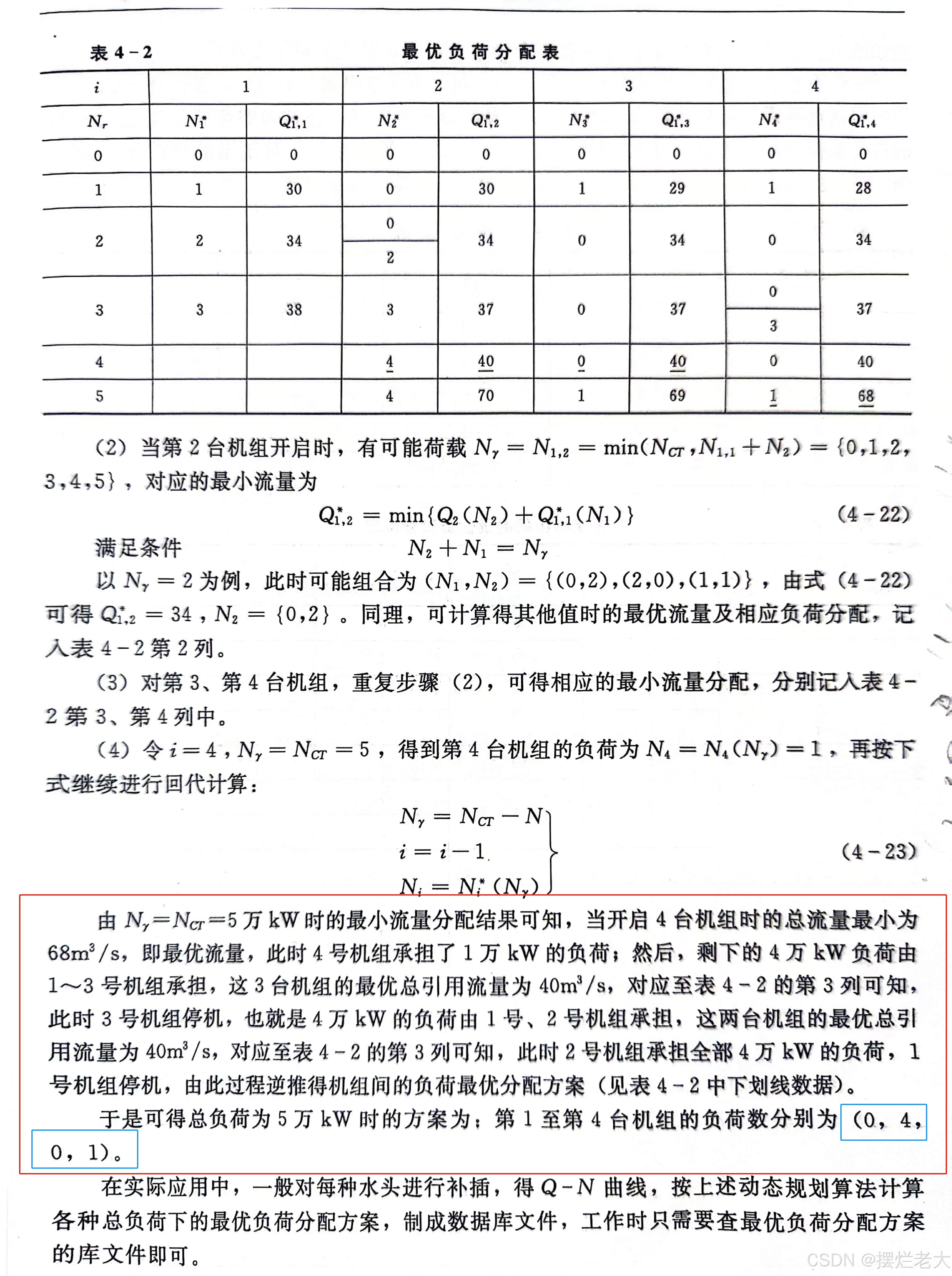
    print(sublist)

由输出结果可以看出，在总负荷为2kw和3kw时，均有两个最优负荷分配方案，对应最小发电流量相同。按照题意，总负荷为5kw时的最有负荷分配方案为（0，4，0，1）。

通过与教材例题的结果进行对比，发现结果一致，说明代码运行准确可行。

3 完整代码

import numpy as np

NCT=5 #最大总负荷kw
# 第一台机组对应装机容量
P1=3
# 第二台机组对应装机容量
P2=4
# ... ...
P3=3
P4=3

# 第一台机组对应负荷的发电流量
Q11=[0,30,34,38] #水流m3/s
# 第二台机组对应负荷的发电流量
Q12=[0,31,34,37,40]
# ... ...
Q13=[0,29,35,38]
Q14=[0,28,35,37]

# 生成各机组对应可能的出力
N1=[i for i in range(0,P1+1)]
N2=[i for i in range(0,P2+1)]
N3=[i for i in range(0,P3+1)]
N4=[i for i in range(0,P4+1)]
# 获取二维表格：出力N对应的流量Q
def get_tab(N,Q):
    tab=np.zeros((len(N),2))
    for i in range (len(N)):
        n=N[i]
        q=Q[i]
        tab[i,0]=n
        tab[i,1]=q
    return tab
tab1=get_tab(N1,Q11)
tab2=get_tab(N2,Q12)
tab3=get_tab(N3,Q13)
tab4=get_tab(N4,Q14)

def plan(NCT):
    lst_Nr=[i for i in range(0,NCT+1)]
    lst_PLAN=[]
    for k in(lst_Nr):
        lst_save = []
        lst_q=[]
        lst_plan = [k]
        for i in(N1):
            for j in(N2):
                 for a in(N3):
                     for b in(N4):
                         if i+j+a+b==k:
                             q1_index=np.where(tab1[:,0] == i)[0]
                             q2_index=np.where(tab2[:,0] == j)[0]
                             q3_index=np.where(tab3[:,0] == a)[0]
                             q4_index=np.where(tab4[:,0] == b)[0]
                             q=tab1[q1_index.item()][1]+tab2[q2_index.item()][1]+tab3[q3_index.item()][1]+tab4[q4_index.item()][1]
                             lst_q.append(q)
                             a_forindex=[i,j,a,b,q]
                             lst_save.append(a_forindex)
        # 列表转换为数组方便找索引
        a_save=np.array(lst_save)
        # 找到流量最小的行索引
        min_row=np.where(a_save[:,4]==min(lst_q))[0]
        # 如果符合if，说明有多个相同的最小值
        if len(min_row)>1:
            # item()用来提取数组的值作为最后的索引
            for i in range(len(min_row)):
                # 将多个方案追加到lst_plan中，比如：k=2时，有两个方案的q最小
                # 都是34，对应lst_save[min_row[i]]的值为[2,0,34]和[0,2,34]
                # 追加之后，首个元素是k=2，代表了当前要求出力N，便有：[2,[2,0,34],[0,2,34]]
                lst_plan.append(lst_save[min_row[i]])
        # 如果只有一个最小值，直接item提取值，索引到相应方案，追加到lst_plan中
        else:
            lst_plan.append(lst_save[min_row.item()])
        lst_PLAN.append(lst_plan)
    lst_PLAN.insert(0, ['N', 'N1', 'N2', 'N3', 'N4', 'Q'])
    return lst_PLAN
result=plan(NCT)
# 遍历嵌套列表，每行输出一个子列表
for sublist in result:
    print(sublist)

本篇博客旨在帮助大家理解练习动态规划在水电站机组最优负荷分配中的应用，在实际的机组最优负荷分配案例中将会有更为复杂的状况，且还要对水头进行离散，计算量将大幅度增加。

以上是全部内容，欢迎大家评论区留言，批评指正。