Codeforces Round 930 (Div. 2 ABCDEF题) 视频讲解

A. Shuffle Party

Problem Statement

You are given an array $a_1,a_2,\dots ,a_n$. Initially, $a_i=i$ for each $1\le i\le n$.

The operation $\text{swap}(k)$ for an integer $k\ge 2$ is defined as follows:

• Let $d$ be the largest divisor${}^{†}$ of $k$ which is not equal to $k$ itself. Then swap the elements $a_d$ and $a_k$.

Suppose you perform $\text{swap}(i)$ for each $i=2,3,\dots ,n$ in this exact order. Find the position of $1$ in the resulting array. In other words, find such $j$ that $a_j=1$ after performing these operations.

${}^{†}$ An integer $x$ is a divisor of $y$ if there exists an integer $z$ such that $y=x\cdot z$.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\le t\le 10^4$). The description of the test cases follows.

The only line of each test case contains one integer $n$ ($1\le n\le 10^9$) — the length of the array $a$.

Output

For each test case, output the position of $1$ in the resulting array.

Example

Example

input
4
1
4
5
120240229

output
1
4
4
67108864

Note

In the first test case, the array is $[1]$ and there are no operations performed.

In the second test case, $a$ changes as follows:

• Initially, $a$ is $[1,2,3,4]$.
• After performing $\text{swap}(2)$, $a$ changes to $[\underline{2},\underline{1},3,4]$ (the elements being swapped are underlined).
• After performing $\text{swap}(3)$, $a$ changes to $[\underline{3},1,\underline{2},4]$.
• After performing $\text{swap}(4)$, $a$ changes to $[3,\underline{4},2,\underline{1}]$.

Finally, the element $1$ lies on index $4$ (that is, $a_4=1$). Thus, the answer is $4$.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

void solve()
{
   
   
	int n;

	cin >> n;

	int i = 1;
	while (i * 2 <= n) i *= 2;

	cout << i << endl;
}

signed main()
{
   
   
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int Data;

	cin >> Data;

	while (Data --)
		solve();

	return 0;
}

---

B. Binary Path

Problem Statement

You are given a $2\times n$ grid filled with zeros and ones. Let the number at the intersection of the $i$-th row and the $j$-th column be $a_{ij}$.

There is a grasshopper at the top-left cell $(1,1)$ that can only jump one cell right or downwards. It wants to reach the bottom-right cell $(2,n)$. Consider the binary string of length $n+1$ consisting of numbers written in cells of the path without changing their order.

Your goal is to:

1. Find the lexicographically smallest${}^{†}$ string you can attain by choosing any available path;
2. Find the number of paths that yield this lexicographically smallest string.

${}^{†}$ If two strings $s$ and $t$ have the same length, then $s$ is lexicographically smaller than $t$ if and only if in the first position where $s$ and $t$ differ, the string $s$ has a smaller element than the corresponding element in $t$.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\le t\le 10^4$). The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2\le n\le 2\cdot 10^5$).

The second line of each test case contains a binary string $a_{11}{a}_{12}\dots a_{1n}$ ($a_{1i}$ is either $0$ or $1$).

The third line of each test case contains a binary string $a_{21}{a}_{22}\dots a_{2n}$ ($a_{2i}$ is either $0$ or $1$).

It is guaranteed that the sum of $n$ over all test cases does not exceed $2\cdot 10^5$.

Output

For each test case, output two lines:

1. The lexicographically smallest string you can attain by choosing any available path;
2. The number of paths that yield this string.

Example

Example

input
3
2
00
00
4
1101
1100
8
00100111
11101101

output
000
2
11000
1
001001101
4

Note

In the first test case, the lexicographically smallest string is $000$. There are two paths that yield this string:

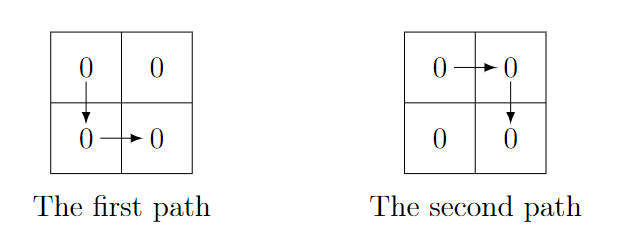
In the second test case, the lexicographically smallest string is $11000$. There is only one path that yields this string:

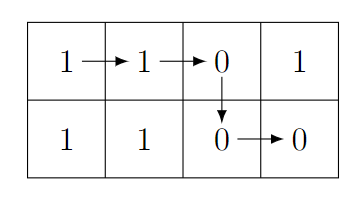
Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

void solve()
{
   
   
	int n;
	string s[2];
	cin >> n >> s[0] >> s[1];

	int p = n - 1;
	for (int i = 1; i < n; i ++)
		if (s[0][i] != '0' && s[1][i - 1] == '0')
		{
   
   
			p = i - 1;
			break;
		}
	string res;
	for (int i = 0; i <= p; i ++)
		res += s[0][i];
	res += s[1][p];
	for (int i = p + 1; i < n; i ++)
		res += s[1][i];

	int lst = 0;
	for (int i = n - 1, j = n; i >= 0; i --, j --)
		if (res[j] != s[1][i])
		{
   
   
			lst = i + 1;
			break;
		}

	cout << res << endl;
	cout << p - lst + 1 << endl;
}

signed main()
{
   
   
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int Data;

	cin >> Data;

	while (Data --)
		solve();

	return 0;
}

---

C. Bitwise Operation Wizard

Problem Statement

There is a secret sequence $p_0,p_1,\dots ,p_{n-1}$, which is a permutation of { 0 , 1 , … , n − 1 } \{0,1,\ldots,n-1\} { 0,1,…,n−1}.

You need to find any two indices $i$ and $j$ such that $p_i\oplus p_j$ is maximized, where $\oplus$ denotes the bitwise XOR operation.

To do this, you can ask queries. Each query has the following form: you pick arbitrary indices $a$, $b$, $c$, and $d$ ($0\le a,b,c,d<n$). Next, the jury calculates $x=(p_a\mid p_b)$ and $y=(p_c\mid p_d)$, where $|$ denotes the bitwise OR operation. Finally, you receive the result of comparison between $x$ and $y$. In other words, you are told if $x<y$, $x>y$, or $x=y$.

Please find any two indices $i$ and j j