Codeforces Round 955 (Div. 2 ABCDEF题) 视频讲解

A. Soccer

Problem Statement

Dima loves watching soccer. In such a game, the score on the scoreboard is represented as $x$ : $y$, where $x$ is the number of goals of the first team, and $y$ is the number of goals of the second team. At any given time, only one team can score a goal, so the score $x$ : $y$ can change to either $(x+1)$ : $y$, or $x$ : $(y+1)$.

While watching a soccer game, Dima was distracted by very important matters, and after some time, he returned to watching the game. Dima remembers the score right before he was distracted, and the score right after he returned. Given these two scores, he wonders the following question. Is it possible that, while Dima was not watching the game, the teams never had an equal score?

It is guaranteed that at neither of the two time points Dima remembers the teams had equal scores. However, it is possible that the score did not change during his absence.

Help Dima and answer the question!

Input

Each test consists of several test cases. The first line contains an integer $t$ ($1\le t\le 10^4$) — the number of test cases. Then follows the description of the test cases.

The first line of each test case contains two integers $x_1,y_1$ ($0\le x_1,y_1\le 10^9$, $x_1\ne y_1$) — the score before Dima was distracted.

The second line of each test case contains two integers $x_2,y_2$ ($x_1\le x_2\le 10^9$, $y_1\le y_2\le 10^9$, $x_2\ne y_2$) — the score when Dima returned.

Output

For each test case, output “YES” without quotes if it is possible, that the teams never had a tie while Dima was away, otherwise output “NO” without quotes.

You can output each letter in any case (for example, the strings “yEs”, “yes”, “Yes”, and “YES” will be recognized as a positive answer).

Example

input
6
1 0
5 0
1 2
3 2
1 2
4 5
1 2
4 3
1 2
1 2
998244353 0
1000000000 999999999

output
YES
NO
YES
NO
YES
YES

Note

In the first test case, the score before Dima left was $1$ : $0$. When he leaves, the first team scores several goals in a row until the score becomes $5$ : $0$, so the answer is YES.

In the second test case, the score could only change as follows:

• $1$ : $2$
• $2$ : $2$
• $3$ : $2$

In this scenario, there is a moment when the teams have an equal score, so the answer is NO.

In the third test case, one of the possible developments is:

• $1$ : $2$
• $1$ : $3$
• $2$ : $3$
• $2$ : $4$
• $2$ : $5$
• $3$ : $5$
• $4$ : $5$

In this scenario, there was no time when the score was equal, so the answer is YES.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

void solve() {
	int lx, ly, x, y;
	cin >> lx >> ly >> x >> y;
	int l1 = x, r1 = lx, l2 = y, r2 = ly;
	if (l1 > r1) swap(l1, r1);
	if (l2 > r2) swap(l2, r2);
	if (l1 >= l2 && r1 <= r2 || l2 >= l1 && r2 <= r1) cout << "NO" << endl;
	else cout << "YES" << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

---

B. Collatz Conjecture

Problem Statement

Note that both of these actions are performed sequentially within one operation.Recently, the first-year student Maxim learned about the Collatz conjecture, but he didn’t pay much attention during the lecture, so he believes that the following process is mentioned in the conjecture:

There is a variable $x$ and a constant $y$. The following operation is performed $k$ times:

• increase $x$ by $1$, then
• while the number $x$ is divisible by $y$, divide it by $y$.

Note that both of these actions are performed sequentially within one operation.

For example, if the number $x=16$, $y=3$, and $k=2$, then after one operation $x$ becomes $17$, and after another operation $x$ becomes $2$, because after adding one, $x=18$ is divisible by $3$ twice.

Given the initial values of $x$, $y$, and $k$, Maxim wants to know what is the final value of $x$.

Input

Each test consists of multiple test cases. The first line contains an integer $t$ ($1\le t\le 10^4$) — the number of test cases. Then follows the description of the test cases.

The only line of each test case contains three integers $x$, $y$, and $k$ ($1\le x,k\le 10^9$, $2\le y\le 10^9$) — the initial variable, constant and the number of operations.

Output

For each test case, output a single integer — the number obtained after applying $k$ operations.

Example

input
13
1 3 1
2 3 1
24 5 5
16 3 2
2 2 1
1337 18 1
1 2 144133
12345678 3 10
998244353 2 998244353
998244353 123456789 998244352
998244354 998241111 998244352
998244355 2 9982443
1000000000 1000000000 1000000000

output
2
1
1
2
3
1338
1
16936
1
21180097
6486
1
2

Note

In the first test case, there is only one operation applied to $x=1$, resulting in $x$ becoming $2$.

In the second test case, for $x=2$, within one operation, one is added to $x$ and it’s divided by $y=3$, resulting in $x$ becoming $1$.

In the third test case, $x$ changes as follows:

• After the first operation, $x=1$, because $24+1=25$ and $25$ is divisible by $y=5$ twice within one operation.
• After the second operation, $x=2$.
• After the third operation, $x=3$.
• After the fourth operation, $x=4$.
• After the fifth operation, $x=1$.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

void solve() {
	int x, y, k;
	cin >> x >> y >> k;
	while (x != 1) {
		int aim = (x / y + 1) * y;
		if (k < aim - x) {
			cout << x + k << endl;
			return;
		} else {
			k -= aim - x, x = aim;
			while (x % y == 0) x /= y;
		}
	}

	k %= (y - x);
	cout << 1 + k << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

---

C. Boring Day

Problem Statement

On another boring day, Egor got bored and decided to do something. But since he has no friends, he came up with a game to play.

Egor has a deck of $n$ cards, the $i$-th card from the top has a number $a_i$ written on it. Egor wants to play a certain number of rounds until the cards run out. In each round, he takes a non-zero number of cards from the top of the deck and finishes the round. If the sum of the numbers on the cards collected during the round is between $l$ and $r$, inclusive, the round is won; otherwise, it is lost.

Egor knows by heart the order of the cards. Help Egor determine the maximum number of rounds he can win in such a game. Note that Egor is not required to win rounds consecutively.

Input

Each test consists of several test cases. The first line contains an integer $t$ ($1\le t\le 10^4$) — the number of test cases. This is followed by a description of the test cases.

The first line of each test case contains three integers $n$, $l$, and $r$ ($1\le n\le 10^5$, $1\le l\le r\le 10^9$).

The second line of each test case contains $n$ integers $a_1,a_2,\dots ,a_n$ ($1\le a_i\le 10^9$) — the numbers on the cards from top to bottom.

It is guaranteed that the sum of $n$ for all test cases does not exceed $2\cdot 10^5$.

Output

For each test case, output a single number — the maximum number of rounds Egor can win.

Example

input
8
5 3 10
2 1 11 3 7
10 1 5
17 8 12 11 7 11 21 13 10 8
3 4 5
3 4 2
8 12 25
10 7 5 13 8 9 12 7
2 3 3
5 2
9 7 9
2 10 5 1 3 7 6 2 3
1 8 10
9
5 5 6
1 4 2 6 4

output
3
0
1
4
0
3
1
2

Note

In the first test case, Egor can win $3$ rounds:

• In the first round, take the top $2$ cards with values $2$ and $1$ and win, as their sum is $3$. After this, the deck will look like this: $[11,3,7]$.
• In the second round, take the top card and lose, as its value $11$ is greater than $r=10$. After this, the deck will look like this: $[3,7]$.
• In the third round, take the top card with value $3$ and win. After this, the deck will look like this: $[7]$.
• After this, in the fourth round, Egor only has to take the last card in the deck with value $7$ and win again.

In the second test case, Egor cannot win any rounds, no matter how hard he tries.

In the third test case, you can take one card in each round, then the first and third rounds will be losing, and the second round will be winning.

In the fourth test case, you can take two cards in each round and always win.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

void solve() {
	int n, L, R;
	cin >> n >> L >> R;
	std::vector<int> a(n + 1, 0);
	for (int i = 1; i <= n; i ++)
		cin >> a[i], a[i] += a[i - 1];

	int m = 1, res = 0;
	while (m <= n) {
		int l = m, r = n;
		while (l < r) {
			int mid = l + r >> 1;
			if (a[mid] - a[m - 1] >= L) r = mid;
			else l = mid + 1;
		}
		if (a[r] - a[m - 1] >= L && a[r] - a[m - 1] <= R) res ++, m = r + 1;
		else m ++;
	}

	cout << res << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

---

D. Beauty of the mountains

Problem Statement

Nikita loves mountains and has finally decided to visit the Berlyand mountain range! The range was so beautiful that Nikita decided to capture it on a map. The map is a table of $n$ rows and $m$ columns, with each cell containing a non-negative integer representing the height of the mountain.

He also noticed that mountains come in two types:

• With snowy caps.
• Without snowy caps.

Nikita is a very pragmatic person. He wants the sum of the heights of the mountains with snowy caps to be equal to the sum of the heights of the mountains without them. He has arranged with the mayor of Berlyand, Polikarp Polikarpovich, to allow him to transform the landscape.

Nikita can perform transformations on submatrices of size $k\times k$ as follows: he can add an integer constant $c$ to the heights of the mountains within this area, but the type of the mountain remains unchanged. Nikita can choose the constant $c$ independently for each transformation. Note that $c$ can be negative.

Before making the transformations, Nikita asks you to find out if it is possible to achieve equality of the sums, or if it is impossible. It doesn’t matter at what cost, even if the mountains turn into canyons and have negative heights.

If only one type of mountain is represented on the map, then the sum of the heights of the other type of mountain is considered to be zero.

Input

Each test consists of several test cases. The first line contains an integer $t$ ($1\le t\le 10^4$) — the number of test cases. This is followed by a description of test cases.

The first line of each test case contains three integers $n,m,k$ ($1\le n,m\le 500,1\le k\le min(n,m)$).

The next $n$ lines of each test case contain $m$ integers $a_{ij}$ ($0\le a_{ij}\le 10^9$) — the initial heights of the mountains.

The next $n$ binary strings of length $m$ for each test case determine the type of mountain, ‘$0$’ — with snowy caps, ‘$1$’ — without them.

It is guaranteed that the sum of $n\cdot m$ for all test cases does not exceed $250000$.

Output

For each test case, output “YES” without quotes if it is possible to equalize the sums of the mountain heights, otherwise output “NO” without quotes. You can output each letter in any case (for example, the strings “yEs”, “yes”, “Yes”, and “YES” will be recognized as a positive answer).

Example

input
8
3 3 2
7 11 3
4 2 3
0 1 15
100
010
000
4 4 3
123 413 24 233
123 42 0 216
22 1 1 53
427 763 22 6
0101
1111
1010
0101
3 3 2
2 1 1
1 1 2
1 5 4
010
101
010
3 3 2
2 1 1
1 1 2
1 5 3
010
101
010
3 4 3
46 49 50 1
19 30 23 12
30 25 1 46
1000
0100
0010
5 4 4
39 30 0 17
22 42 30 13
10 44 46 35
12 19 9 39
21 0 45 40
1000
1111
0011
0111
1100
2 2 2
3 4
6 7
00
00
2 2 2
0 0
2 0
01
00

output
YES
NO
YES
NO
YES
NO
YES
YES

Note

The mountain array from the first test case looks like this:

Initially, the sum of the heights of the mountains with snowy caps is $11+3+4+3+0+1+15=37$, and without them is $7+2=9$.

To equalize these sums, we can perform two transformations:

First transformation:

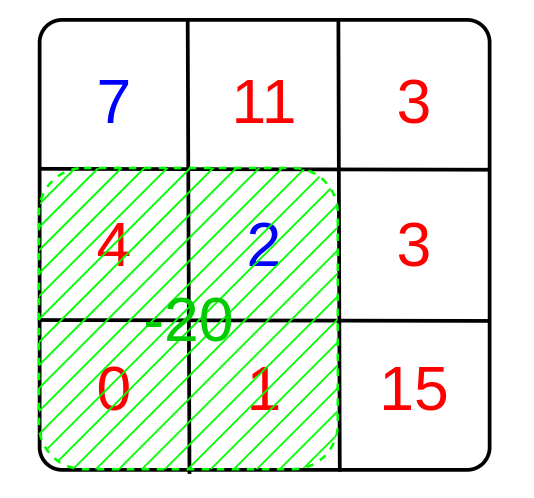
Note that the constant $c$ can be negative.

After the first transformation, the mountain array looks like this:

Second transformation:

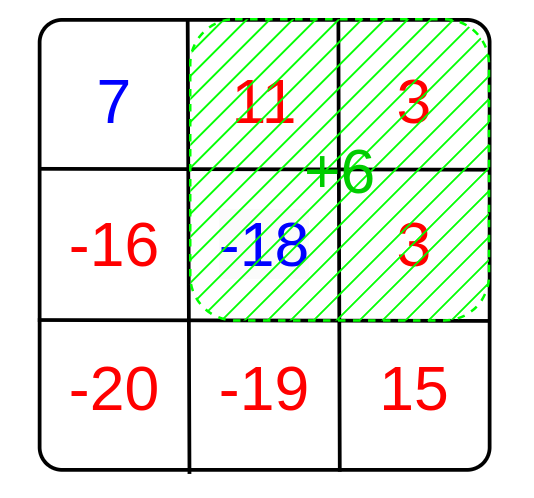
As a result, the mountain array looks like this:

The sum of the heights of the mountains with snowy caps is $17+9+9-16-20-19+15=-5$, and without them is $7-12=-5$, thus the answer is YES.

Solution

具体见文后视频。

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 5e2 + 10;

int n, m, k;
int a[N][N], b[N][N];

void solve() {
	cin >> n >> m >> k;
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
			cin >> a[i][j];
	char x;
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++) {
			cin >> x, b[i][j] = (x ^ 48), b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
			if (x & 1) a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] - a[i][j];
			else a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + a[i][j];
		}
	int d = 0;
	for (int i = k; i <= n; i ++)
		for (int j = k; j <= m; j ++)
			d = __gcd(d, abs(k * k - 2 * (b[i][j] - b[i - k][j] - b[i][j - k] + b[i - k][j - k])));

	a[n][m] = abs(a[n][m]);
	if (!d) {
		if (a[n][m] == 0) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	else if (a[n][m] % d == 0) cout << "YES" << endl;
	else cout << "NO" << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

---

E. Number of k-good subarrays

Problem Statement

Let $bit(x)$ denote the number of ones in the binary representation of a non-negative integer $x$.

A subarray of an array is called $k$-good if it consists only of numbers with no more than $k$ ones in their binary representation, i.e., a subarray $(l,r)$ of array $a$ is good if for any $i$ such that $l\le i\le r$ condition $bit(a_i)\le k$ is satisfied.

You are given an array $a$ of length $n$, consisting of consecutive non-negative integers starting from $0$, i.e., $a_i=i$ for $0\le i\le n-1$ (in $0$-based indexing). You need to count the number of $k$-good subarrays in this array.

As the answer can be very large, output it modulo $10^9+7$.

Input

Each test consists of multiple test cases. The first line contains an integer $t$ ($1\le t\le 10^4$) — the number of test cases. The following lines describe the test cases.

The single line of each test case contains two integers $n$, $k$ ($1\le n\le 10^{18},1\le k\le 60$).

Output

For each test case, output a single integer — the number of $k$-good subarrays modulo $10^9+7$.

Example

input
10
6 1
16 2
1 1
3 1
31 3
14 1
1337 5
100000 20
795569939321040850 56
576460752303423268 59

output
7
35
1
6
155
8
7323
49965
741136395
66679884

Note

For the first test case $a=[0,1,2,3,4,5]$, $k=1$.

To find the answer, let’s write all the numbers in binary representation:

$$a=[000,001,010,011,100,101]$$

From this, it can be seen that the numbers $3$ and $5$ have $2\ge (k=1)$ ones in their binary representation, so the answer should include all subarrays that do not contain either $3$ or $5$, which are the subarrays (in $0$-based indexing): ($0$, $0$), ($0$, $1$), ($0$, $2$), ($1$, $1$), ($1$, $2$), ($2$, $2$), ($4$, $4$).

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 62, mod = 1e9 + 7;

struct Info {
	int len, l, r, cnt;
	Info operator+ (const Info &tmp) {
		Info res;
		res.len = len + tmp.len;
		res.l = len == l ? tmp.l + l : l, res.r = tmp.len == tmp.r ? r + tmp.r : tmp.r;
		res.cnt = (cnt + tmp.cnt + (r % mod) * (tmp.l % mod) % mod) % mod;
		return res;
	}
}f[N][N];

Info getf(int n, int k) {
	if (k >= 0) return f[n][k];
	return {1ll << n, 0, 0, 0};
}
void solve() {
	int n, k;
	cin >> n >> k;

	Info res = {0, 0, 0, 0};
	int s = 0;
	for (int i = 60; i >= 0; i --)
		if (n >> i & 1) {
			res = res + getf(i, k - s);
			s ++;
		}

	cout << res.cnt << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	for (int i = 0; i < N; i ++)
		f[0][i] = {1, 1, 1, 1};
	for (int i = 1; i < N; i ++)
		for (int j = 0; j < N; j ++)
			f[i][j] = getf(i - 1, j) + getf(i - 1, j - 1);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

---

F. Sorting Problem Again

Problem Statement

You have an array $a$ of $n$ elements. There are also $q$ modifications of the array. Before the first modification and after each modification, you would like to know the following:

What is the minimum length subarray that needs to be sorted in non-decreasing order in order for the array $a$ to be completely sorted in non-decreasing order?

More formally, you want to select a subarray of the array $(l,r)$ with the minimum value of $r-l+1$. After that, you will sort the elements $a_l,a_{l+1},\dots ,a_r$ and want the condition $a_i\le a_{i+1}$ to hold for all $1\le i<n$. If the array is already sorted in non-decreasing order, then $l$ and $r$ should be considered as equal to $-1$.

Note that finding such $(l,r)$ does not change the array in any way. The modifications themselves take the form: assign $a_{pos}=x$ for given $pos$ and $x$.

Input

Each test consists of several test cases. The first line contains an integer $t$ ($1\le t\le 10$) — the number of test cases. Then follows the description of test cases.

The first line of each test case contains a single integer $n$ ($1\le n\le 5\cdot 10^5$).

The second line of each test case contains $n$ integers $a_i$ ($0\le |a_i|\le 10^9$) — the initial elements of the array $a$.

The third line of each test case contains a number $q$ ($0\le q\le 5\cdot 10^5$) — the number of modifications to the array.

The following $q$ lines of each test case contain two integers $po{s}_i$ ($1\le po{s}_i\le n$) and $va{l}_i$ ($0\le |va{l}_i|\le 10^9$) — this means that for the $i$-th modification, $a_{po{s}_i}$ is assigned the value $va{l}_i$.

It is guaranteed that the sum of $n$ and the sum of $q$ for all test cases does not exceed $5\cdot 10^5$.

Output

For each test case, output $q+1$ lines. Each line should contain $2$ integers $l,r$ — the boundaries of the minimum subarray, such that sorting it will make the array $a$ completely sorted. If $a$ is already sorted, then output $l=-1$, $r=-1$.

Example

input
2
5
2 2 3 4 5
3
2 1
4 1
1 1
5
1 2 3 4 5
9
1 4
2 3
5 2
3 1
1 1
5 1
4 1
3 1
2 1

output
-1 -1
1 2
1 4
3 4
-1 -1
1 3
1 3
1 5
1 5
2 5
2 5
2 5
2 5
-1 -1

Note

Let’s consider the first test case:

• Initially, the array is sorted in non-decreasing order: $[2,2,3,4,5]$
• After the first query, the array looks like this: $[2,1,3,4,5]$.
• After the second query, the array looks like this: $[2,1,3,1,5]$.
• After the third query, the array looks like this: $[1,1,3,1,5]$.

The red segments indicate the subarrays that need to be sorted in order for the entire array to be sorted in non-decreasing order.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 5e5 + 10, INF = 2e9;

int n, q;
int a[N], mn[N << 2], mx[N << 2];

void pushup(int u) {
	mn[u] = min(mn[u << 1], mn[u << 1 | 1]);
	mx[u] = max(mx[u << 1], mx[u << 1 | 1]);
}
void modify(int u, int l, int r, int x, int d) {
	if (l == r) mn[u] = mx[u] = d;
	else {
		int mid = l + r >> 1;
		if (mid >= x) modify(u << 1, l, mid, x, d);
		else modify(u << 1 | 1, mid + 1, r, x, d);
		pushup(u);
	}
}
PII query(int u, int l, int r, int ql, int qr) {
	if (l >= ql && r <= qr) return {mn[u], mx[u]};
	int mid = l + r >> 1, rmn = INF, rmx = -INF;
	if (mid >= ql) {
		auto tmp = query(u << 1, l, mid, ql, qr);
		rmn = min(rmn, tmp.fi), rmx = max(rmx, tmp.se);
	}
	if (mid < qr) {
		auto tmp = query(u << 1 | 1, mid + 1, r, ql, qr);
		rmn = min(rmn, tmp.fi), rmx = max(rmx, tmp.se);
	}
	return {rmn, rmx};
}
void solve() {
	cin >> n;
	set<int> pos;
	memset(mn, -0x3f, sizeof mn), memset(mx, 0x3f, sizeof mx);
	for (int i = 1; i <= n; i ++) {
		cin >> a[i], modify(1, 1, n, i, a[i]);
		if (i > 1 && a[i] < a[i - 1]) pos.insert(i);
	}

	if (!pos.size()) cout << -1 << " " << -1 << endl;
	else {
		int l = *pos.begin(), r = *pos.rbegin();
		auto tmp = query(1, 1, n, l - 1, r);
		int L = upper_bound(a + 1, a + l, tmp.fi) - a, R = lower_bound(a + r + 1, a + 1 + n, tmp.se) - a - 1;
		cout << L << " " << R << endl;
	}
	cin >> q;
	while (q -- ) {
		int p, v;
		cin >> p >> v;
		a[p] = v, modify(1, 1, n, p, v);
		if (p > 1 && a[p] < a[p - 1]) pos.insert(p);
		if (p > 1 && a[p] >= a[p - 1] && pos.count(p)) pos.erase(p);
		if (p < n && a[p + 1] < a[p]) pos.insert(p + 1);
		if (p < n && a[p + 1] >= a[p] && pos.count(p + 1)) pos.erase(p + 1);
		if (!pos.size()) {
			cout << -1 << " " << -1 << endl;
			continue;
		}
		int l = *pos.begin(), r = *pos.rbegin();
		auto tmp = query(1, 1, n, l - 1, r);
		int L = upper_bound(a + 1, a + l, tmp.fi) - a, R = lower_bound(a + r + 1, a + 1 + n, tmp.se) - a - 1;
		cout << L << " " << R << endl;
	}
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

---

视频讲解

Codeforces Round 955 (Div. 2)（A ~ F 题讲解）

---

最后祝大家早日