文章详细介绍了快速排序算法的三种不同实现方式：Hoare版本、挖坑法和前后指针版本，包括各自的代码实现。同时，讨论了快速排序的时间复杂度，并提出了针对有序或接近有序数组的优化策略，如三数取中和在小规模时切换排序算法。
目录
1.hoare版本
快速排序是一种二叉树结构的交换排序方法，其基本思想为：
任取待排序元素序列中的某元素作为基准值（一般取数组首元素），按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
以升序为例，当选取左边第一个元素做基准值时，右边先走去找数组中比基准值小的值，右边先走是为了保证相遇的位置的值比基准值小。
相遇分两种情况
一种是R 停住，L在寻找比基准值大的值时遇到R，相遇的位置就是R停住的位置。这种情况是R找到了一个比基准值小的元素等待L去找一个比基准值大的元素，与R所在位置的元素进行交换，如果L与R相遇了，就表示没有找到，这时R与L相遇的位置的值是比基准值是要小的。
一种是L停住了，R在寻找比基准值小的值时遇到L，相遇的位置就是L停住的位置。这种情况是L找到了一个比基准值大的元素等待R去找一个比基准值小的元素，与L所在位置的元素进行交换，如果R与L相遇了，就表示没有找到，这时R与L相遇的位置的值是比基准值是要大的。
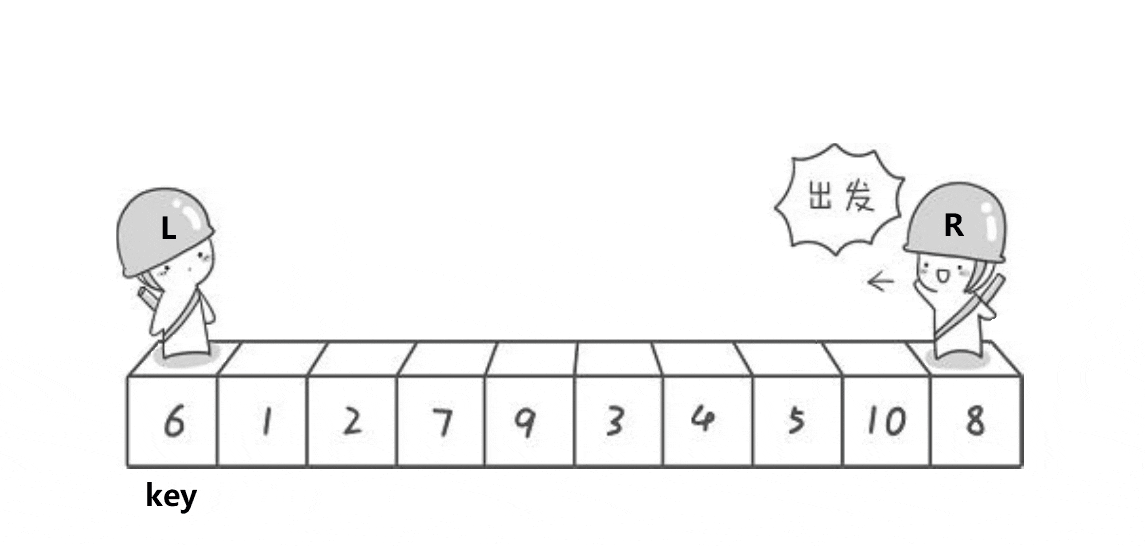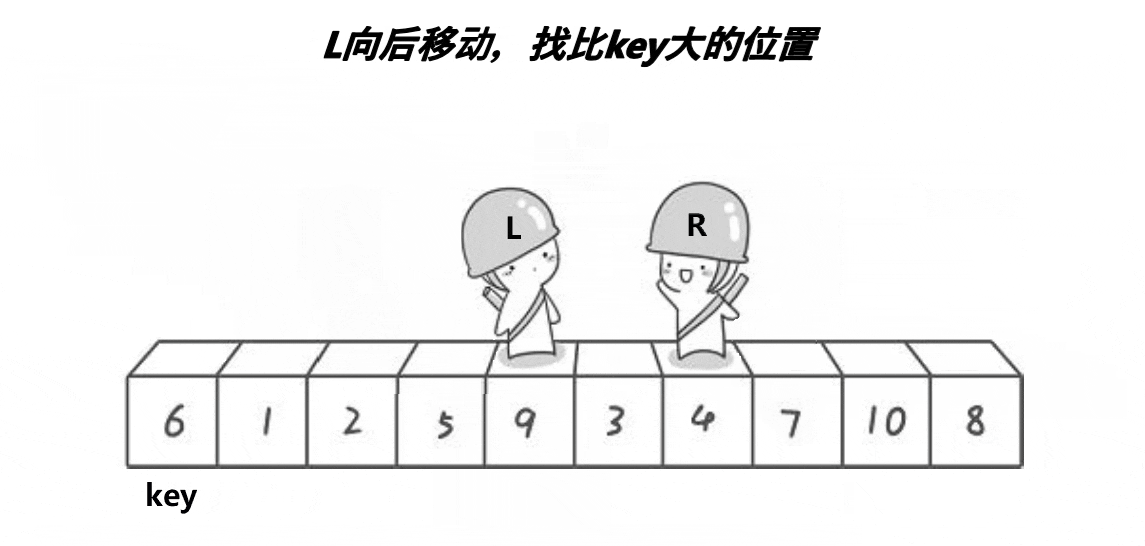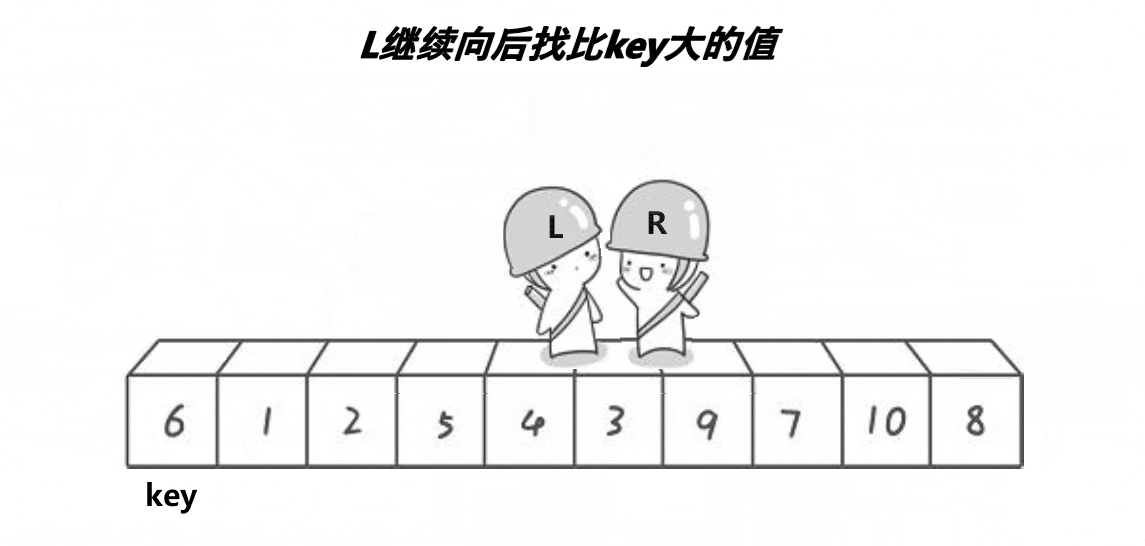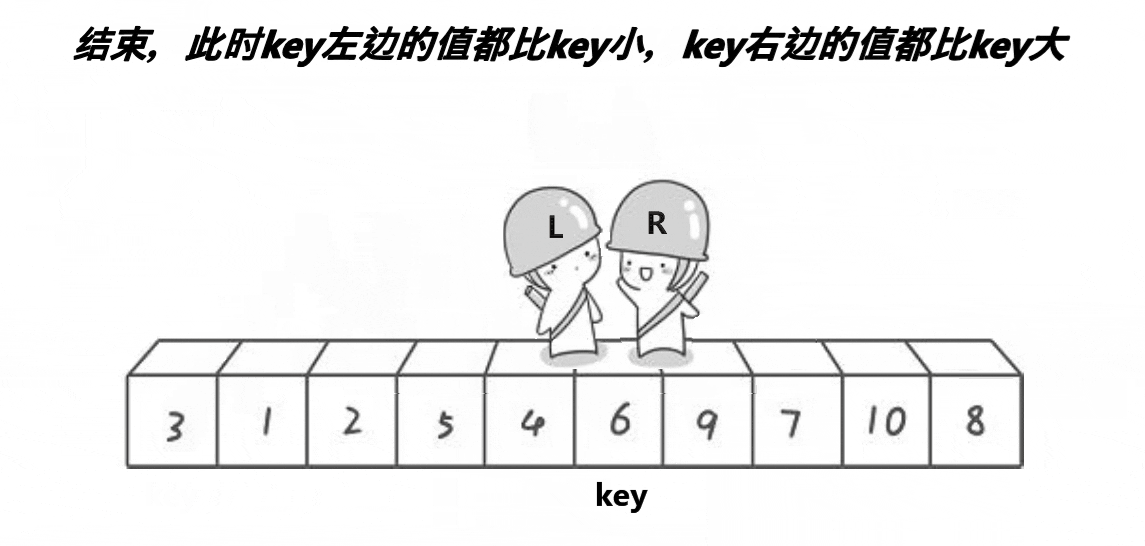
单趟排序
经过单趟排序后，分割出了：
1.比Key值小的左子序列,key值,比key值大的右子序列
2.这时的key值的位置就是排序后的位置了，也就是说在之后的排序中都不再对key值做进行操作。
3.只要左右区间有序那么整体就有序，接下来的操作就是对左右子序列进行排序。
void swap(int* r, int* h)
{
int tmp;
tmp = *r;
*r = *h;
*h = tmp;
}
void quicsort(int *a,int begin,int end)
{
if (begin >= end)
{
return;
}
int left = begin, right = end;
int keyi = left;
while (left < right)
{
//右边先走，找小
while (left < right&&a[right] >= a[keyi])
{
--right;
}
//找大
while (left < right&&a[left] <= a[keyi])
{
++left;
}
swap(&a[left], &a[right]);
}
swap(&a[left], &a[keyi]);
keyi = left;
quicsort(a, begin, keyi - 1);
quicsort(a, keyi +1,end);
}
时间复杂度
最坏情况(以升序为例)
对于规模N的数组，如果数组有序的话，这时是最环情况，因为每次右子序列规模只比原数组少一个元素素，导致递归次数变多，
每次分割后，数组都会被划分为一个大小为0的左子序列和比原数组少一个元素的右子序列。
设要排序规模为N的数组所花费的时间T（N)，那T（N）等于分割数组时花的时间加左右子序列所花的时间，分割数组时会遍历数万花时间为O（N）
所以 T（N）=T（O)+T(N-1)+0(N)。
现在只需要算出T（N)即可
将上式各项相加
最好情况就是每次选到一个基准值刚好位于中间，此时两个子数组刚好是原数组的一半，那么T（N）= 2*T（N/2）+O(N)
优化
优化1：当数组有序或接近有序时快排的时间复杂度为O（N^2)，那我们如何优化？
三数取中
所谓的三数取中，是指在待排数组中的首元素和最后一个元素以及中间位置，在这三个位置中选取元素数大小排在中间的值，做为基准值这样就可以防止O（N^2)的情况出现
优化2：
在使用快速排序排到小区间时，使用其他的排序方法辅助排序，减少递归。
hoare版本完整代码
#include<stdio.h>
void swap(int* r, int* h)
{
int tmp;
tmp = *r;
*r = *h;
*h = tmp;
}
//三数取中 最左begin 最右end 中间mid
//三个数中第二大的数
int GetMidindex(int *a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] > a[end])
{
return begin;
}
else//a[end]>a[begin]
return end;
}
else//a[begin]>a[mid]
{
if (a[mid] > a[end])
{
return mid;
}
else if(a[end]>a[mid])
{
return end;
}
else//a[begin]<a[end]
{
return begin;
}
}
}
//hoare版本
void quicsort1(int *a,int begin,int end)
{
if (begin >= end)
{
return;
}
if ((end - begin + 1) < 10)
{
//调用插入排序
}
else//小区间优化
{
int mid = GetMidindex(a, begin, end);
swap(&a[begin], &a[mid]);
int left = begin, right = end;
int keyi = left;
while (left < right)
{
//右边先走，找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
//找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
swap(&a[left], &a[right]);
}
swap(&a[left], &a[keyi]);
keyi = left;
quicsort1(a, begin, keyi - 1);
quicsort1(a, keyi + 1, end);
}
}
int main()
{
int a[] = {943, 3,11,21,55,88,109,302,13,16,11,21,55,88,109,302,13,16 };
quicsort1(a, 0, sizeof(a)/sizeof(int)-1);
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ",a[i]);
}
return 0;
}
2.挖坑法
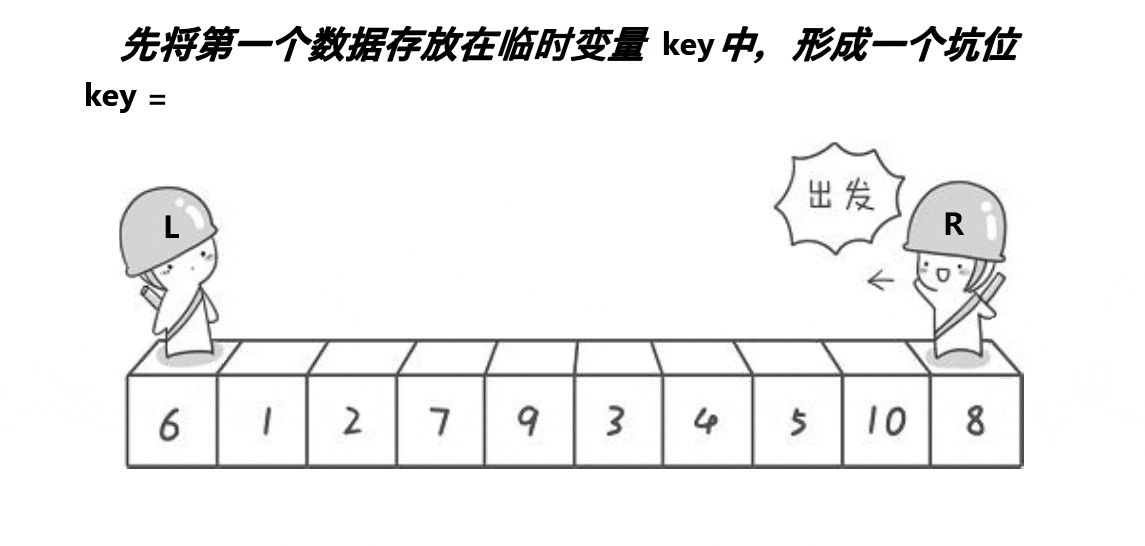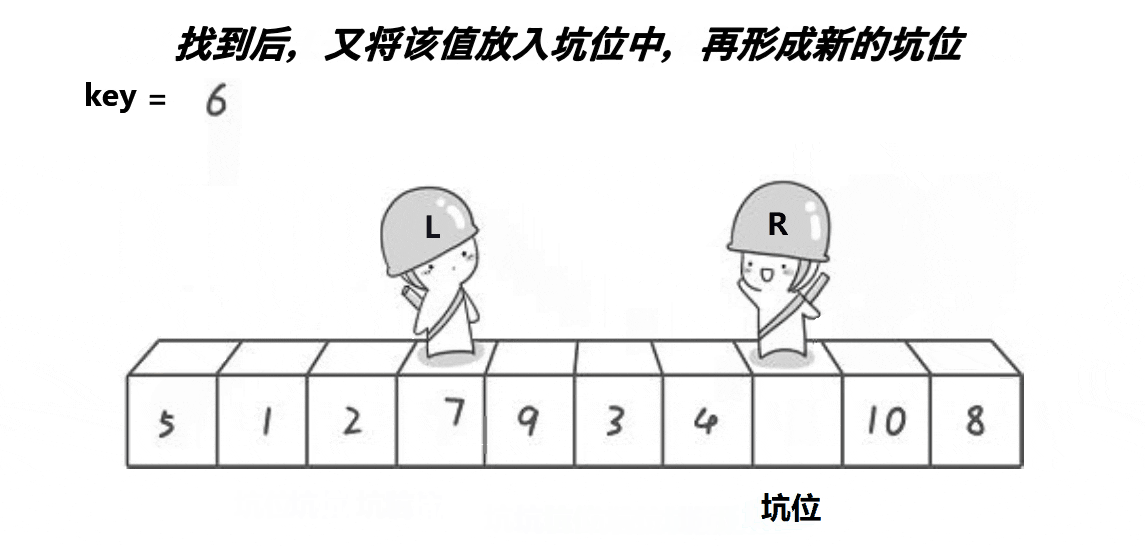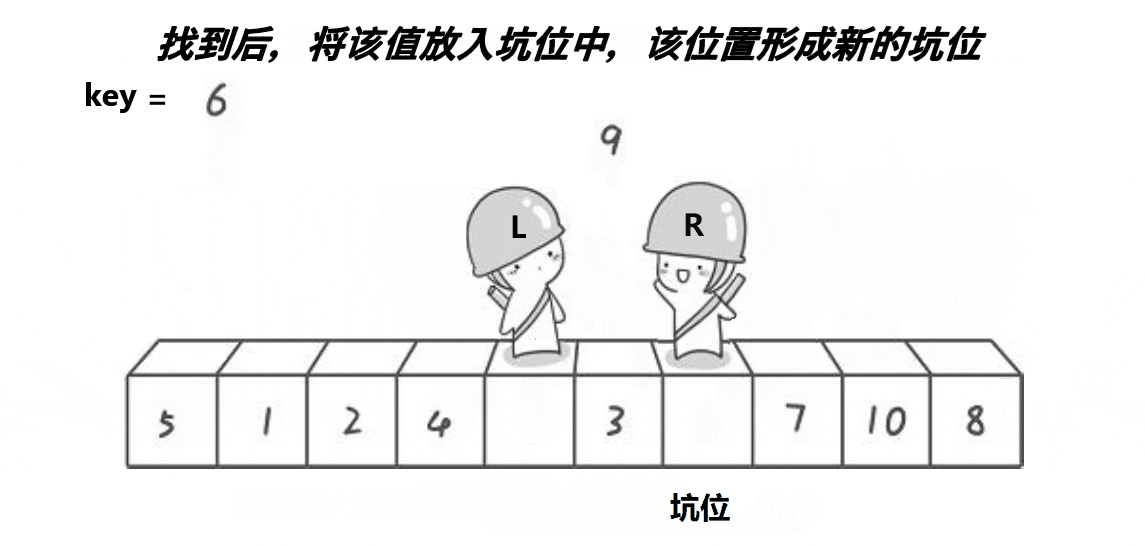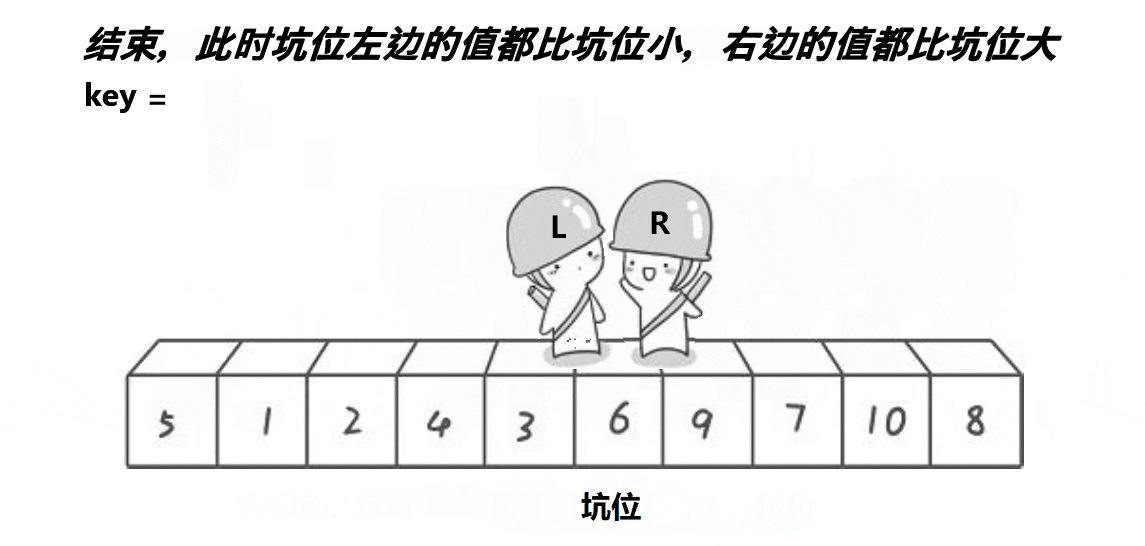
挖坑法完整代码
#include<stdio.h>
void swap(int* r, int* h)
{
int tmp;
tmp = *r;
*r = *h;
*h = tmp;
}
//三数取中 最左begin 最右end 中间mid
//三个数中第二大的数
int GetMidindex(int *a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] > a[end])
{
return begin;
}
else//a[end]>a[begin]
return end;
}
else//a[begin]>a[mid]
{
if (a[mid] > a[end])
{
return mid;
}
else if(a[end]>a[mid])
{
return end;
}
else//a[begin]<a[end]
{
return begin;
}
}
}
//挖坑
int PartSort2(int* a, int begin, int end)
{
int mid = GetMidindex(a, begin, end);
swap(&a[begin], &a[mid]);
int left = begin, right = end;
int key = a[left];
int hole = left;
while (left < right)
{
// 右边找小，填到左边坑里面
while (left < right && a[right] >= key)
{
--right;
}
a[hole] = a[right];
hole = right;
// 左边找大，填到右边坑里面
while (left < right && a[left] <= key)
{
++left;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
//if ((end - begin + 1) < 15)
//{
// // 小区间用直接插入替代，减少递归调用次数
// //InsertSort(a + begin, end - begin + 1);
//}
else
{
int keyi = PartSort2(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}
int main()
{
int a[] = {943, 3,11,21,55,88,109,302,13,16,11,21,55,88,109,302,13,16 };
QuickSort(a, 0, sizeof(a)/sizeof(int)-1);
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ",a[i]);
}
return 0;
}3. 前后指针版本
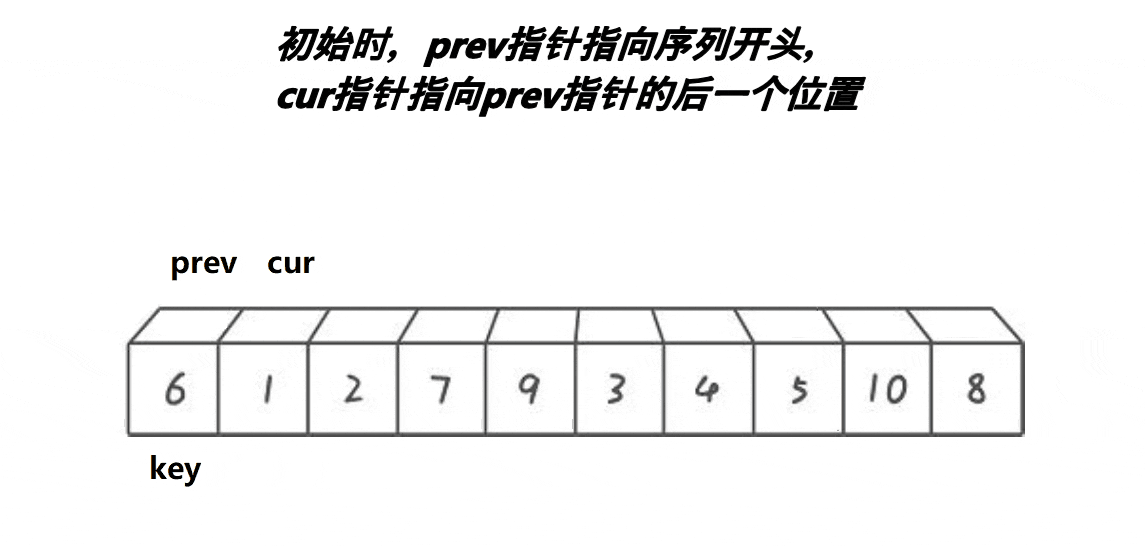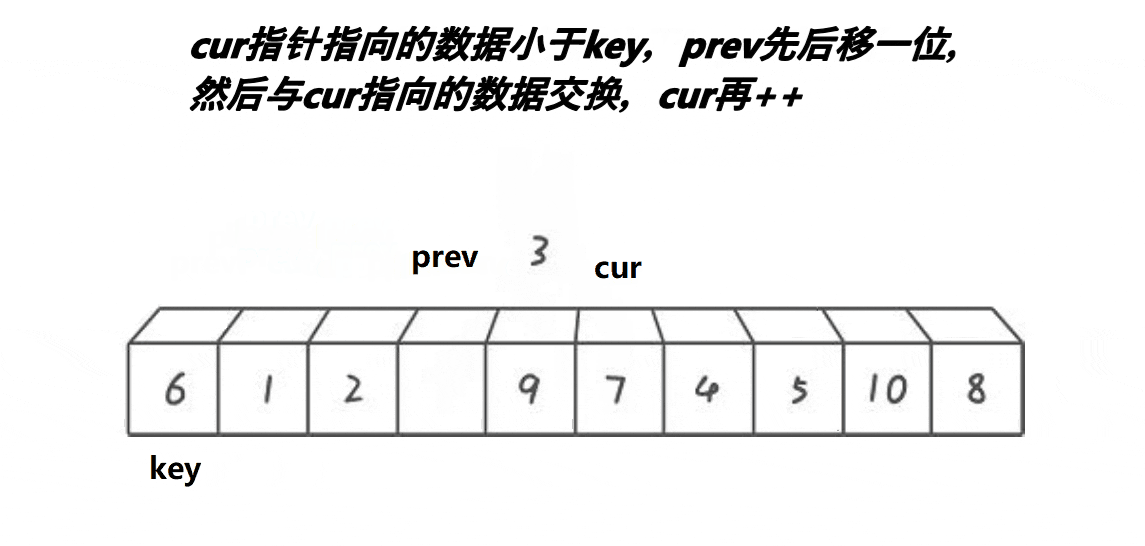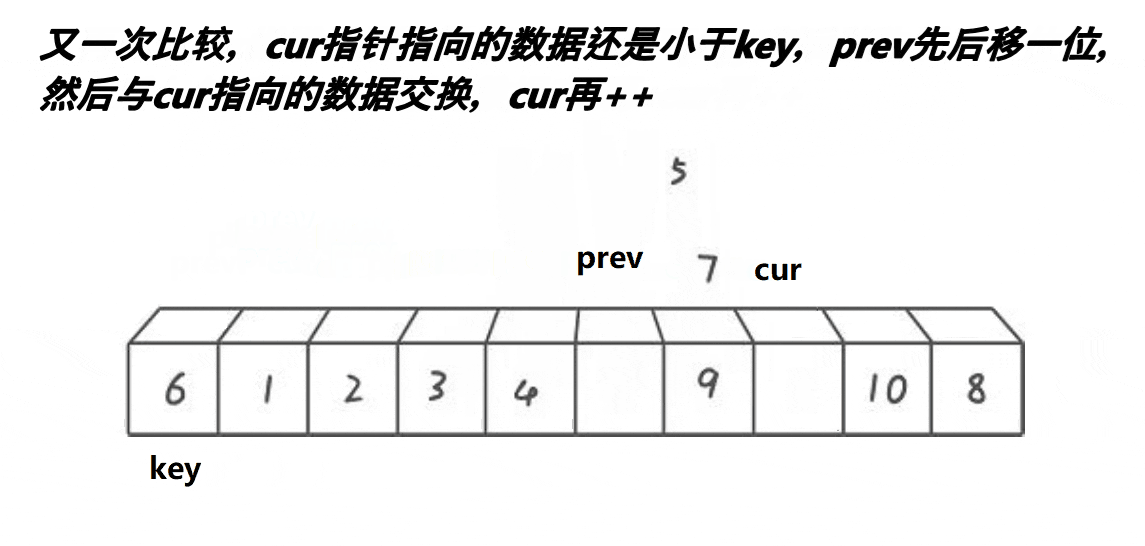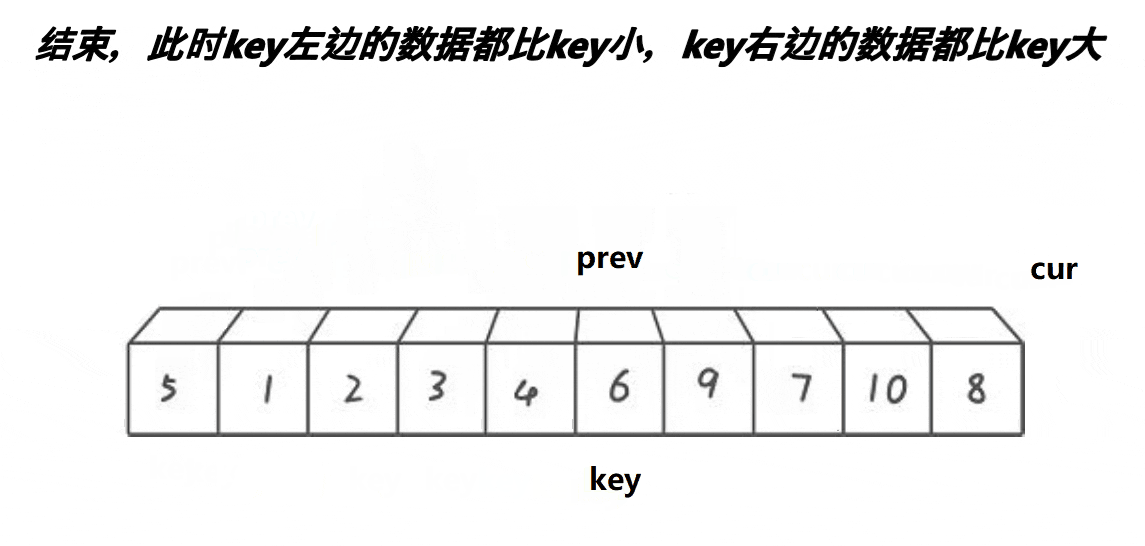
单趟排序
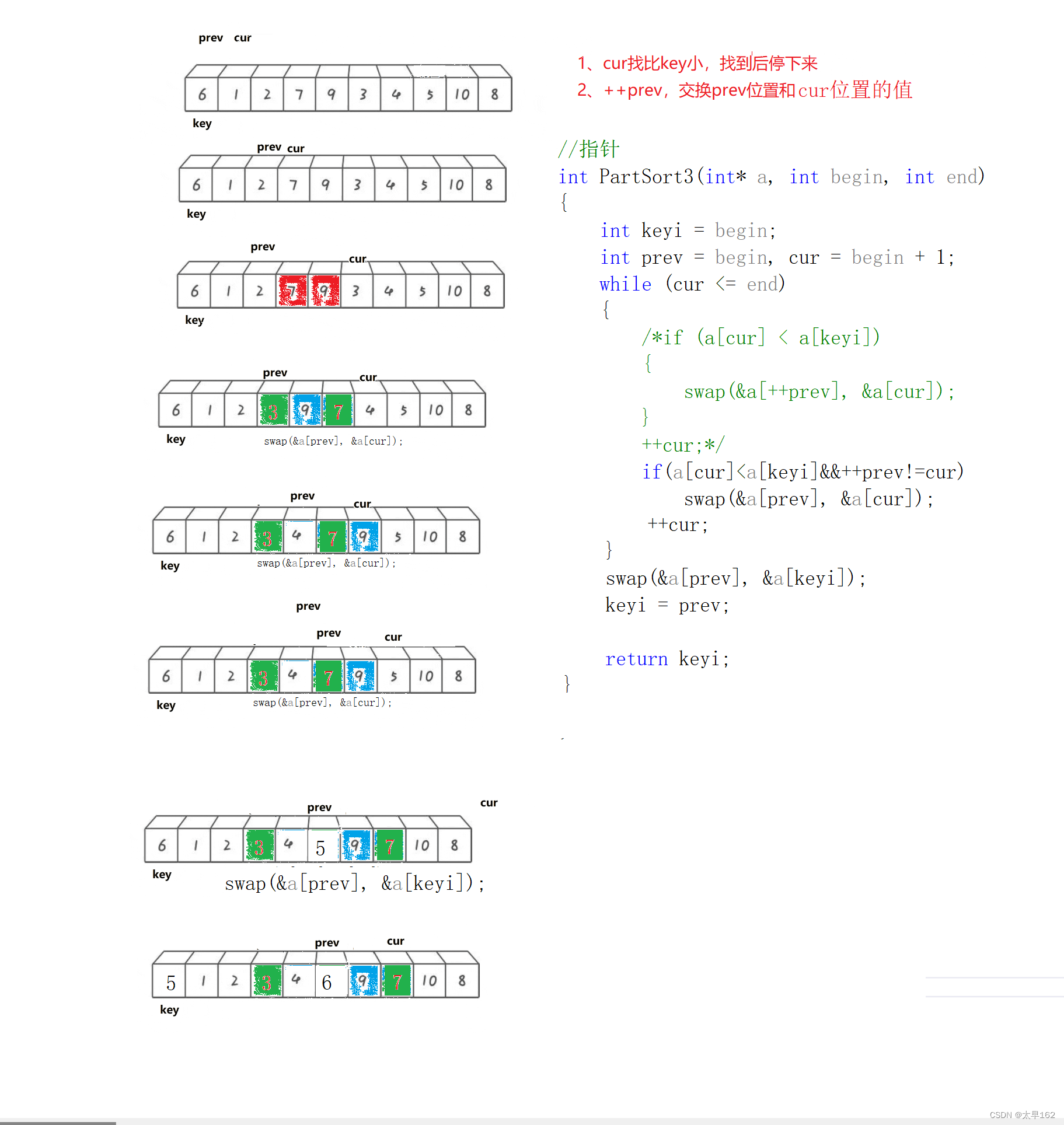
前后指针版本完整代码
#include<stdio.h>
void swap(int* r, int* h)
{
int tmp;
tmp = *r;
*r = *h;
*h = tmp;
}
//指针
int PartSort3(int* a, int begin, int end)
{
int keyi = begin;
int prev = begin, cur = begin + 1;
while (cur <= end)
{
if(a[cur]<a[keyi]&&++prev!=cur)
swap(&a[prev], &a[cur]);
++cur;
}
swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
//if ((end - begin + 1) < 15)
//{
// // 小区间用直接插入替代，减少递归调用次数
// //InsertSort(a + begin, end - begin + 1);
//}
else
{
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}
int main()
{
int a[] = {943, 3,11,21,55,88,109,302,13,16,11,21,55,88,109,302,13,16 };
QuickSort(a, 0, sizeof(a)/sizeof(int)-1);
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ",a[i]);
}
return 0;
}
扫一扫
1092
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
