问题 F: 图的最短路径-Floyd算法输出最短路径包含的边

题目描述

在Floyd算法求解图的最短路径过程中，会记录两个顶点之间最短路径所经过的边。
如下图例子所示，本题给出Floyd算法的最后结果，请求出任意两点之间最短路径长度，以及相应的最短路径所包含的边。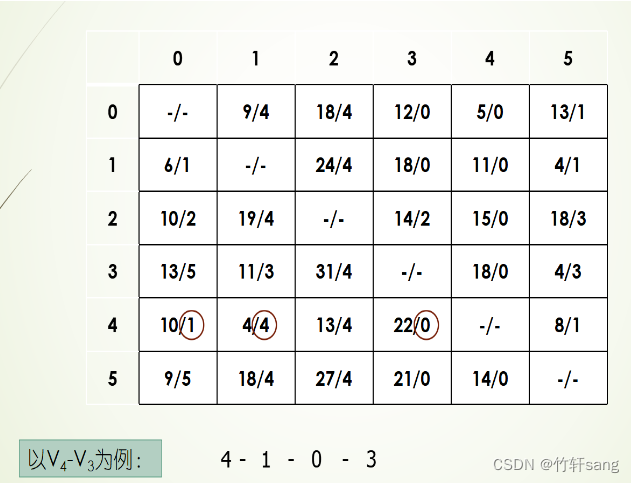 

输入格式

输入第一行为正整数n，表示图的节点数量（小于100）
接下来是n*n的矩阵，每个元素包含两个整数，分别是两点之间最短路径长度，和路径经过的中间节点。
最后是两个整数p和q，表示两个顶点序号。

输出格式

第一行输出从顶点p到顶点q的最短路径长度。
第二行输出该最短路径经过的边对应的顶点序列。

输入样例

6
-1 -1 9 4 18 4 12 0 5 0 13 1
6 1 -1 -1 24 4 18 0 11 0 4 1
10 2 19 4 -1 -1 14 2 15 0 18 3
13 5 11 3 31 4 -1 -1 18 0 4 3
10 1 4 4 13 4 22 0 -1 -1 8 1
9 5 18 4 27 4 21 0 14 0 -1 -1
4 3

输出样例  

22
4 1 0 3 

代码展示 

#include<iostream>
#include<bits/stdc++.h>
#include<vector>
#include<utility>
#include<climits>
using namespace std;


int main(){
    //freopen("/config/workspace/test/test","r",stdin);
    int n;
    cin>>n;
	
	int a[n][n*2];
	for(int i=0;i<n;i++){
		for(int j=0;j<n*2;j++){
			cin>>a[i][j];
		}
	}

	int p,q;
	cin>>p>>q;

	cout<<a[p][q*2]<<endl;

	stack<int>path;
	path.push(q);
	for(int i=p,j=q;a[i][j*2+1]!=p;j=a[i][j*2+1]){
		path.push(a[p][j*2+1]);
	}
	path.push(p);
	while(!path.empty()){
		cout<<path.top()<<" ";
		path.pop();
	}


    return 0;
}

//闲叙题外话：怎么有点头疼...