C语言青蛙跳台阶详解

一 递归方式实现

青蛙跳台阶,可以一次跳一个台阶,也可以一次跳两个台阶,现在有N个台阶,请问青蛙有多少种跳台阶的方式?
分析问题:

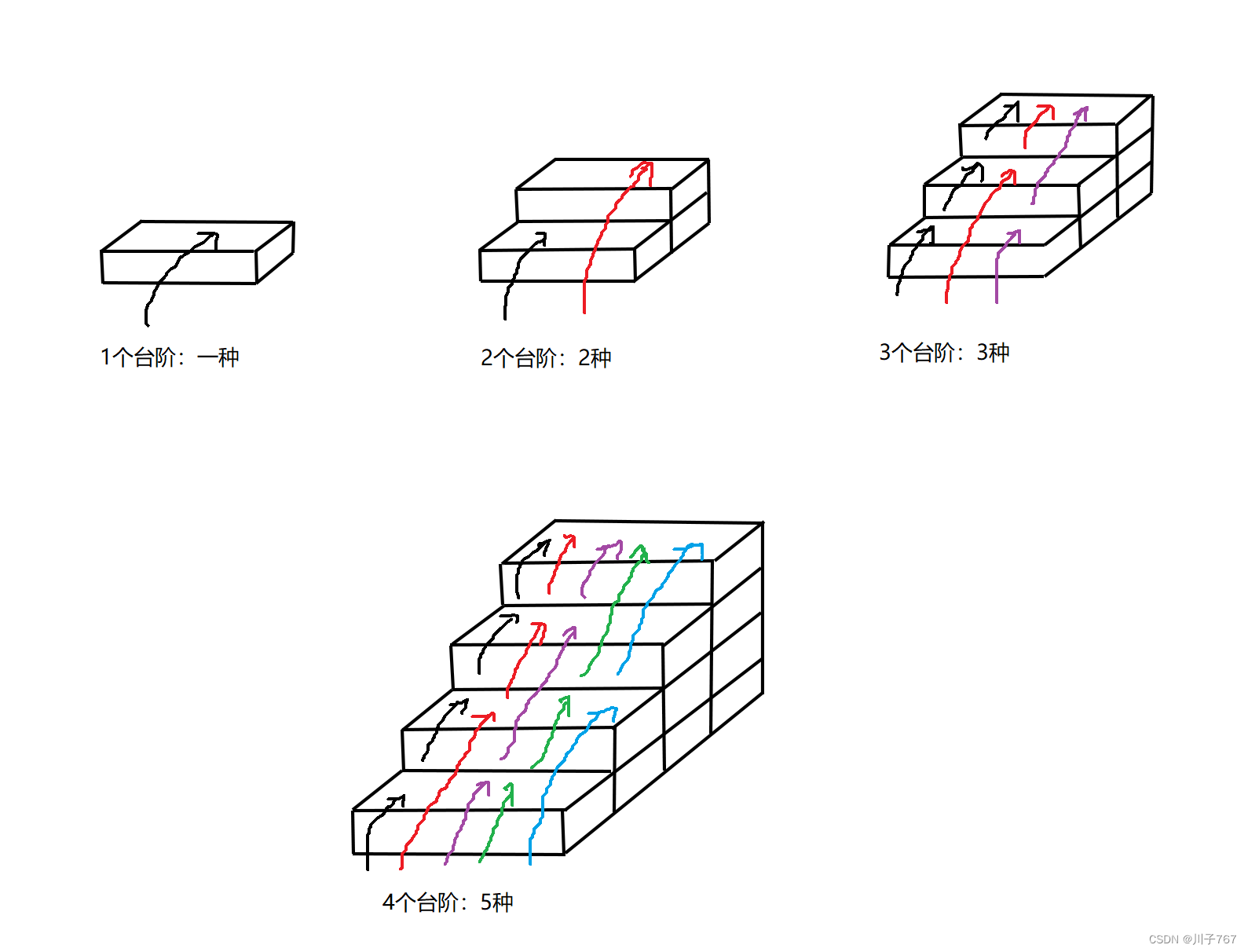
由上图可知:

台阶个数	方法个数	公式
1	1	n
2	2	n
3	3	1+2
4	5	2+3
n	…	(n-2)+(n-1)

第n个台阶的方法个数是n的前两个数的和,也就是f(n-2)+(n-1),这个公式和求第n个斐波那契数列是同种思路,相当于是斐波那契数列的变种;而第一项和第二项的方法个数都是台阶的个数,这样就很好写代码啦
递归实现的代码:

#include<stdio.h>
int D_step(int n)
{
	if (n <= 2)
		return n;
	else
		return D_step(n - 1) + D_step(n - 2);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = D_step(n);
	printf("%d", ret);
	return 0;
}

二 非递归方式实现

n的前两个数之和是n个台阶的方法数,a=1,b=2,c=a+b;
然后把b的值赋值给a,把c的值赋值给b,n–,直到n的值小于等于2结束.

非递归实现的代码:

#include<stdio.h>
int FD_step(int n)
{
	int a = 1;
	int b = 2;
	int c = 0;
	while (n > 2)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	return c;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = FD_step(n);
	printf("%d", ret);
	return 0;
}

三 总结

其实青蛙跳台阶这个问题,可以通过找规律来解决,通过上述发现,青蛙跳台阶问题其实就是斐波那契数列的变种,和斐波那契数列的思想一样,找到规律来解决这个问题就非常简单啦~