在前文 Graph Neural Networks 中,我们采用GNN架构建立了模型求解节点分类问题。在本文中,我们将讨论GNN架构的局限性,这将帮助我们了解提出GCN架构的动机。之后,我们将介绍GCN架构是如何工作的,并探究其优于GNN架构的原因。最后,我们将GCN架构运用于Cora数据集中,观察模型的性能,并将GCN架构运用于节点回归中,观察其表现。
文章目录
前言
图卷积网络(GCN)架构是GNN的蓝图。它基于创建卷积神经网络(CNN)应用于图的有效变体的想法。更准确地说,它是图信号处理中图卷积运算的近似。由于其通用性和易用性,GCN已成为科学文献中最受欢迎的GNN。并且,它往往是面对图数据时的基线模型。
提示:以下是本篇文章正文内容,下面案例可供参考
一、图卷积层
首先观察GNN层:
h
i
=
∑
j
∈
N
i
x
j
W
T
h_i=\sum_{j\in N_i}{x_jW^T}
hi=j∈Ni∑xjWT
可以发现我们并没有考虑邻居数量的差异,GNN层由一个没有任何归一化系数的简单和组成。
假设节点1有1000个邻居,节点2只有1个邻居,此时,节点1的嵌入向量
h
A
h_A
hA会比节点2的嵌入向量
h
B
h_B
hB拥有更多更大的数值。这会导致问题当我们在比较两者的嵌入向量时。因此,为了进行更有意义的比较,我们将嵌入向量除于邻居的数量,写作
d
e
g
(
A
)
deg(A)
deg(A),其具体的表示如下:
h
i
=
1
d
e
g
(
i
)
∑
j
∈
N
i
x
j
W
T
h_i=\frac{1}{deg\left( i \right)}\sum_{j\in N_i}{x_jW^T}
hi=deg(i)1j∈Ni∑xjWT
转化为矩阵乘法,写作:
H
=
D
~
−
1
A
~
X
W
T
或者
H
=
A
~
D
~
−
1
X
W
T
H=\tilde{D}^{-1}\tilde{A}XW^T 或者 H=\tilde{A}\tilde{D}^{-1}XW^T
H=D~−1A~XWT或者H=A~D~−1XWT
式中:
A
~
=
A
+
I
\tilde{A}=A+I
A~=A+I 表示邻接矩阵和自循环矩阵之和。左侧表示归一化每一行的特征,右侧表示归一化每一列的特征。
然而,上式会导致有很多邻居的节点更容易传播,而孤立的节点不易传播。因此,赋予更高的权重予以更少邻居的节点,上式变更为:
H
=
D
~
−
1
2
A
~
T
D
~
−
1
2
X
W
T
H=\tilde{D}^{-\frac{1}{2}}\tilde{A}^T\tilde{D}^{-\frac{1}{2}}XW^T
H=D~−21A~TD~−21XWT
二、Cora分类数据集
1、导入数据库
import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch.nn.functional as F
import torch_geometric.transforms as T
import seaborn as sns
from scipy.stats import norm
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import degree
from torch_geometric.utils import to_dense_adj
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import FacebookPagePage
from torch_geometric.datasets import WikipediaNetwork
from sklearn.metrics import mean_squared_error, mean_absolute_error
from collections import Counter
np.random.seed(42)
torch.manual_seed(42)
torch.cuda.manual_seed(42)
torch.cuda.manual_seed_all(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
2、观察数据集
我们导入Cora的数据集,并可视化各节点的邻居节点个数。
# Import dataset from PyTorch Geometric
dataset = Planetoid(root=".", name="Cora")
data = dataset[0]
# Get list of neighbors for each node
degrees = degree(data.edge_index[0]).numpy()
# adjacency = to_dense_adj(data.edge_index)[0]
# Count the number of nodes for each degree
numbers = Counter(degrees)
# Bar plot
fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()

3、分类GCN架构
提出GCN类如下。
def accuracy(y_pred, y_true):
"""Calculate accuracy."""
return torch.sum(y_pred == y_true) / len(y_true)
class GCN(torch.nn.Module):
"""Graph Convolutional Network"""
def __init__(self, dim_in, dim_h, dim_out):
super().__init__()
# deg_inv_sqrt = deg.pow_(-0.5)
# adj_t = torch_sparse.mul(adj_t, deg_inv_sqrt.view(-1, 1))
# adj_t = torch_sparse.mul(adj_t, deg_inv_sqrt.view(1, -1))
self.gcn1 = GCNConv(dim_in, dim_h)
self.gcn2 = GCNConv(dim_h, dim_out)
def forward(self, x, edge_index):
h = self.gcn1(x, edge_index)
h = torch.relu(h)
h = self.gcn2(h, edge_index)
return F.log_softmax(h, dim=1)
def fit(self, data, epochs):
# cross-entropy loss
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(self.parameters(),
lr=0.01, # a learning rate
weight_decay=5e-4) # L2 regularization
self.train()
losses = []
accs = []
val_losses = []
val_accs = []
for epoch in range(epochs+1):
optimizer.zero_grad()
out = self(data.x, data.edge_index)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
acc = accuracy(out[data.train_mask].argmax(dim=1),
data.y[data.train_mask])
loss.backward()
optimizer.step()
val_loss = criterion(out[data.val_mask], data.y[data.val_mask])
val_acc = accuracy(out[data.val_mask].argmax(dim=1),
data.y[data.val_mask])
print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | Train Acc:'
f' {acc*100:>5.2f}% | Val Loss: {val_loss:.2f} | '
f'Val Acc: {val_acc*100:.2f}%')
losses.append(loss)
accs.append(acc)
val_losses.append(val_loss)
val_accs.append(val_acc)
self.train_loss = losses
self.train_acc = accs
self.val_loss = val_losses
self.val_acc = val_accs
@torch.no_grad()
def test(self, data):
self.eval()
out = self(data.x, data.edge_index)
acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
return acc
下述备注内容,体现了GCN层的运算特征。
deg_inv_sqrt = deg.pow_(-0.5)
adj_t = torch_sparse.mul(adj_t, deg_inv_sqrt.view(-1, 1))
adj_t = torch_sparse.mul(adj_t, deg_inv_sqrt.view(1, -1))
4、训练GCN分类模型
# Create the Vanilla GNN model
gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)
# Train
gcn.fit(data, epochs=100)
# Test
acc = gcn.test(data)
print(f'\nGCN test accuracy: {acc*100:.2f}%\n')
# plot
num = range(1, len(gcn.train_loss)+1)
plt.plot(num, np.array(gcn.train_loss), label="Training loss")
plt.plot(num, np.array(gcn.val_loss), ":", label="Val loss")
plt.title("GCN Training and validation loss")
plt.style.use('seaborn-colorblind')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
plt.plot(num, np.array(gcn.train_acc), label="Training acc")
plt.plot(num, np.array(gcn.val_acc), ':', label="Val acc")
plt.style.use('seaborn-colorblind')
plt.title("GCN Training and validation acc")
plt.xlabel("Epochs")
plt.ylabel("acc")
plt.legend()
plt.show()
运行上述代码,可以得到训练结果如图2所示。


三、Wikipedia Network回归数据集
数据来自英文版维基百科(2018年12月)。这些数据集代表特定主题(变色龙、鳄鱼和松鼠)的页面-页面网络。节点代表物品,边是物品之间的相互链接。边csv文件包含边-节点从o开始索引。特征json文件包含文章的特征,每个键是一个页面id,节点特征以列表的形式给出。在特征列表中出现一个特征意味着在维基百科文章的文本中出现了一个信息性名词。目标csv包含节点标识符和每个页面在2017年10月至2018年11月之间的月平均流量。
1、观察数据集
# Wikipedia Network
dataset = WikipediaNetwork(root=".",
name="chameleon",
transform = T.RandomNodeSplit(num_val=200, num_test=500))
data = dataset[0]
path = "F:\Python_eBook\Graph Neural Networks\Dataset\wikipedia\chameleon\musae_chameleon_target.csv"
df = pd.read_csv(path)
values = np.log10(df['target'])
data.y = torch.tensor(values)
# Get list of degrees for each node
degrees = degree(data.edge_index[0]).numpy()
# Count the number of nodes for each degree
numbers = Counter(degrees)
# Bar plot
fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()
df['target'] = values
fig = sns.distplot(df['target'], fit=norm)
plt.show()
在上述代码中,将网站的日流量作为预测目标,并同时用对数函数处理目标值。
在回归问题中,检验目标值的分布是必须的,非正态分布的目标值较难预测。


2、回归GCN架构
基于GCN回归建立类。
# GCN class
class GCN(torch.nn.Module):
"""Graph Convolutional Network"""
def __init__(self, dim_in, dim_h, dim_out):
super().__init__()
self.gcn1 = GCNConv(dim_in, dim_h*4)
self.gcn2 = GCNConv(dim_h*4, dim_h*2)
self.gcn3 = GCNConv(dim_h*2, dim_h)
self.linear = torch.nn.Linear(dim_h, dim_out)
def forward(self, x, edge_index):
h = self.gcn1(x, edge_index)
h = torch.relu(h)
h = F.dropout(h, p=0.5, training=self.training)
h = self.gcn2(h, edge_index)
h = torch.relu(h)
h = F.dropout(h, p=0.5, training=self.training)
h = self.gcn3(h, edge_index)
h = torch.relu(h)
h = self.linear(h)
return h
def fit(self, data, epochs):
optimizer = torch.optim.Adam(self.parameters(),
lr=0.02,
weight_decay=5e-4)
self.train()
losses = []
val_losses = []
for epoch in range(epochs+1):
optimizer.zero_grad()
out = self(data.x, data.edge_index)
loss = F.mse_loss(out.squeeze()[data.train_mask], data.y[data.train_mask].float())
loss.backward()
optimizer.step()
val_loss = F.mse_loss(out.squeeze()[data.val_mask], data.y[data.val_mask])
print(f"Epoch {epoch:>3} | Train Loss: {loss:.5f} | Val Loss: {val_loss:.5f}")
losses.append(loss)
val_losses.append(val_loss)
self.train_loss = losses
self.val_loss = val_losses
def test(self, data):
self.eval()
out = self(data.x, data.edge_index)
return F.mse_loss(out.squeeze()[data.test_mask], data.y[data.test_mask].float())
在上述代码中,加深GCN卷积层并逐层减小神经元的数量,这样设置的目的是为了使得强迫模型去选择同目标值预测高度相关的输入特征。
3、训练GCN回归模型
# Create the Vanilla GNN model
gcn = GCN(dataset.num_features, 128, 1)
print(gcn)
# Train
gcn.fit(data, epochs=200)
# Test
loss = gcn.test(data)
print(f'\nGCN test loss: {loss:.5f}\n')
# plot
num = range(1, len(gcn.train_loss)+1)
plt.plot(num[20:], np.array(gcn.train_loss[20:]), label="Training loss")
plt.plot(num[20:], np.array(gcn.val_loss[20:]), ":", label="Val loss")
plt.title("GCN Training and validation loss")
plt.style.use('seaborn-colorblind')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
# evaluate
out = gcn(data.x, data.edge_index)
y_pred = out.squeeze()[data.test_mask].detach().numpy()
mse = mean_squared_error(data.y[data.test_mask], y_pred)
mae = mean_absolute_error(data.y[data.test_mask], y_pred)
print('=' * 43)
print(f'MSE = {mse:.4f} | RMSE = {np.sqrt(mse):.4f} | MAE = {mae:.4f}')
print('=' * 43)
fig = sns.regplot(x=data.y[data.test_mask].numpy(), y=y_pred)
fig.set(xlabel='Ground truth', ylabel='Predicted values')
plt.show()

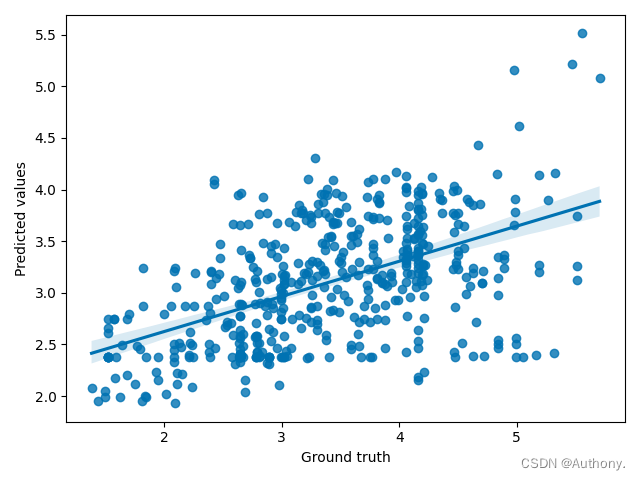
MSE = 0.7000 | RMSE = 0.8367 | MAE = 0.6409
总结
在本文中,我们改进了我们的GNN层来正确地规范化特征。这个增强引入了GCN层和智能规范化。我们将这个新架构与我们在Cora数据集上的GNN进行了比较。由于这种归一化过程,GCN在这种情况下都获得了最高的准确率分数。最后,我们将其应用于维基百科网络的节点回归,并学习如何处理这个新任务。
























 5171
5171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








