词法分析器3-正规式到词法分析器_词法分析器正规式-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_64343068/article/details/134408425

对于有限自动机，目标是使得从一组正规式导出可执行词法分析器的过程自动化。这一节，将开发一些构造法，以便将RE转换为适合于实现的FA，还将设计一种算法，从FA接受的语言推导出对应的RE。

要解释这些构造法，我们需要先了解NFA和DFA。

3.1 NFA和DFA

对于RE的定义，规定 $\epsilon$ 为RE，但是我们之前手工构建的FA都不包含 $\epsilon$ ，但一些RE确实用到了 $\epsilon$ 。

FA在S1->S2的转移不会消耗任何字符，目测我们可以合并这两个状态，形成下图：

举例：对于a*和ab的FA

可以用一个 $\epsilon$ 转移合并它们，形成一个处理a*ab的FA

$\epsilon$ 的引入使得S0在遇到字母a时可以有两种转移：1）转移到S0 2）转移到S2。

识别ab和aab的转移是不同的。采取哪一种转移取决于a后面的那个字符。对于包含S0这种状态的FA称为NFA。

NFA：非确定有限自动机：对单个输入字符有多种可能的转移；弧上的标记可以是 $\sum$ 中的一个字，而不一定是单个字符；初态不唯一，终态集可空。

DFA：确定有限自动机：每个状态对任一输入字符都具有唯一可能的转移；初态唯一，终态集合可空。

注：NFA和DFA在表达力上是等价的，任何DFA都是某个NFA的一个特例。

3.2 正规式与NFA

3.21 正规式->NFA

对于 $\sum$ 上的正规式，我们将构造一个NFA M，使L(M)=L(r)，并且M只有一个终态，而且没有从该终态出发的箭弧。

1）转换模板

2）引入两个新的状态：初态和终态

3）若RE中没有运算符，转换图3.11

4）举例：a(b|c)*

手工生成的NFA如下图，与上述NFA相比简洁很多，后续会对上述NFA进行简化。

正规式->NFA构造的特性：

（1）每个NFA都有一个起始状态和接受状态。

（2）除了进入起始状态的初始转移之外，没有其他转移；没有从接受状态发出的转移。

（3）在连接早先构建的对应于一些组件RE的NFA时，总是使用 $\epsilon$ 转移来连接前一个NFA的接受状态和后一个NFA的起始状态。

（4）每个状态至多有两个进入该状态和两个退出该状态的 $\epsilon$ 转移，对于字母表中的每个符号，至多有一个进入该状态和一个退出该状态的转移。

3.22 NFA->正规式

对于 $\sum$ 上的NFA M，我们来构造 $\sum$ 上的正规式r，使L(r)=L(M)

（1）转换模板

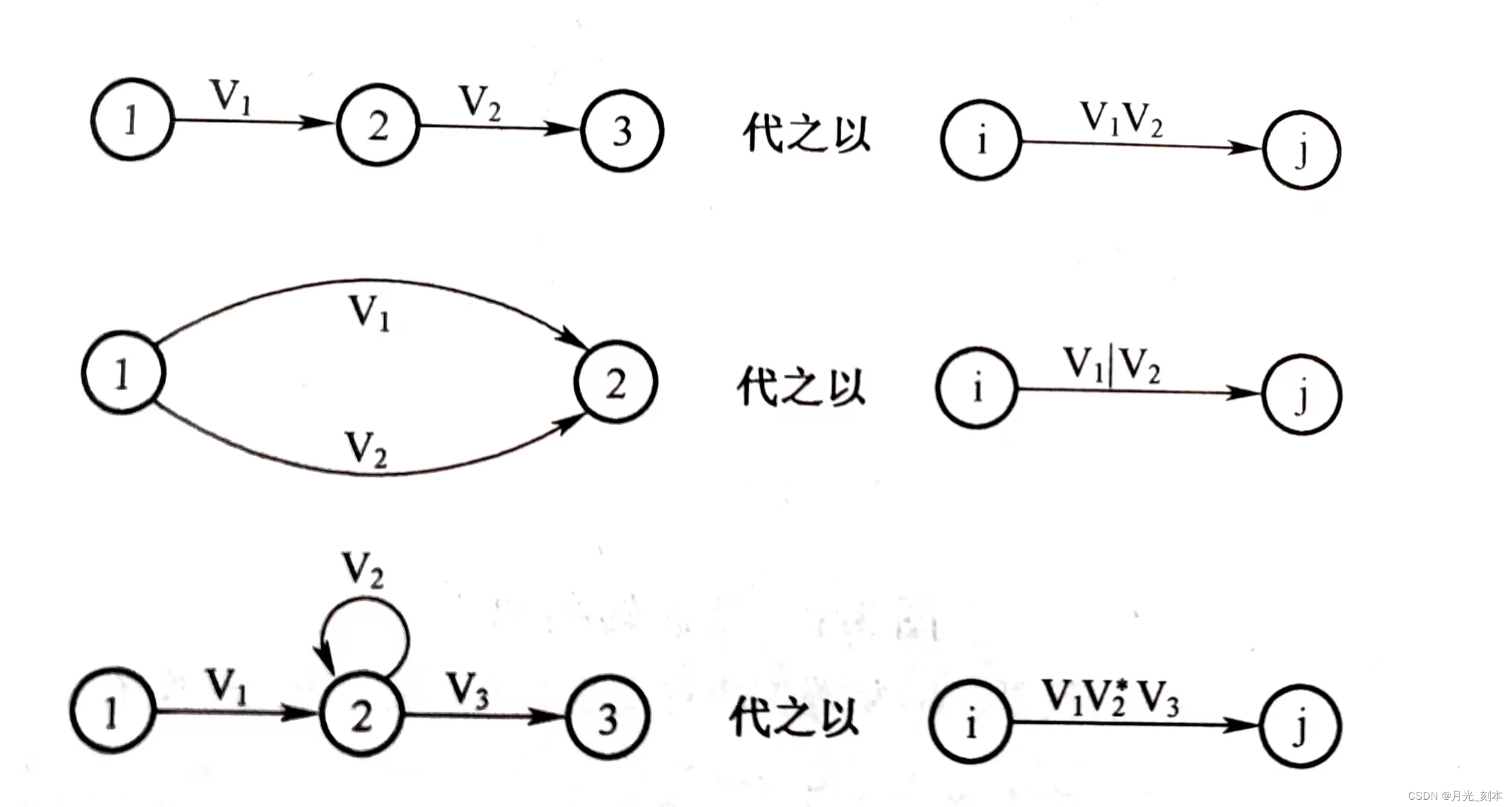
（2）在M的转换图上加入两个状态，初态X，终态Y。从X用 $\epsilon$ 弧连接到M的所有初态；从M的所有终态结点用 $\epsilon$ 弧连接到Y，从而形成一个新的NFA，记为M‘

（3）反复利用（1）的转换规则，逐步消去M’中的所有结点，直至只剩下X和Y为止。

3.3 NFA->DFA:子集法

识别RE定义的语言，与NFA的执行相比，DFA的执行要容易模拟的多，所以在构造法的循环中，下一步是将NFA转换为可以识别同一语言的DFA。

NFA和DFA使用同样的字母表 $\sum$ ，DFA的起始状态和接受状态集是通过构造逐渐得到的，比较复杂的是从NFA的状态集推导DFA的状态集，以及DFA的转移函数的推导。

3.31 步骤

（1）转换模板

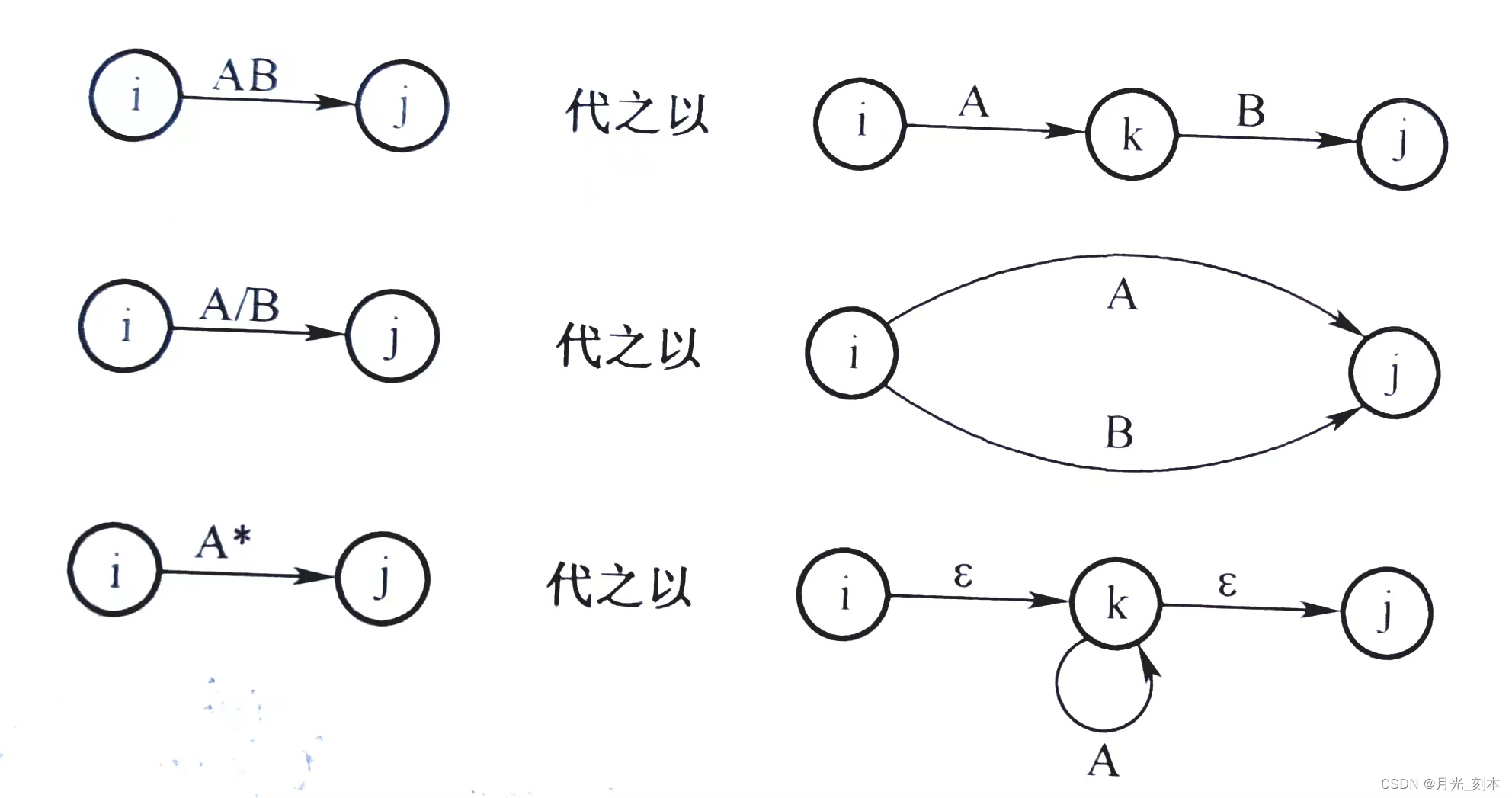
（2）引入新的初态结点X和终态结点Y；从X到So（NFA的初态集）中任意结点连一条 $\epsilon$ 箭弧，从F（NFA的终态集）中任意结点连一条 $\epsilon$ 箭弧到Y，然后重复（1）的分裂过程，直到状态转换图的每条箭弧上的标记为 $\epsilon$ 或 $\sum$ 中的单个字母。将得到的NFA记为M‘。

（3）构造闭包

>定义状态集I的闭包： $\epsilon$ _CLOSURE(I)=I U J。（J：I中节点经过任意 $\epsilon$ 到达的结点的集合）

>I的字符a可达的状态集：Ia= $\epsilon$ _CLOSURE(J)。（J：I中节点经过一条a弧到达的结点的集合）

>重构状态转移图

①该算法从一个初始集合I0开始，其中包含了X（M‘的初始状态），以及在M’中X通过仅包含 $\epsilon$ 转移（一条或多条连续仅包含 $\epsilon$ 的弧）的路径所能到达的所有状态。

②计算经过字符可达的状态集：假设字符a，接下来计算Ia，其中包含初态集合I0中每一个元素经过一条a弧能直接到达的状态，接下来求目前Ia中所有元素的闭包，即其中元素经过仅包含 $\epsilon$ 转移（一条或多条连续仅包含 $\epsilon$ 的弧）的路径所能到达的所有状态，将这些状态也加入到Ia中，到此Ia结束。计算I0的其他字符到达集。

③接下来依次计算已经得到的到达集的字符到达集。一直重复③直到没有新的到达集出现。

3.32 举例

（1）引入X和Y状态，并进行分裂后的结果如下：

（2）子集构造法

初始集合I0：包含X和X的闭包，{X，5，1}

Ia：{5，3}（I0中的每个元素经过一条a弧能直接到达的状态） U {1}（已得到的Ia{5，3}中每个元素求闭包，在此只有5有闭包）= {5，3，1}

I	Ia	Ib
{X,5,1}	{5,3,1}	{5,4,1}
{5,3,1}	{5,3,1,2,6,Y}	{5,4,1}
{5,4,1}	{5,3,1}	{5,4,1,2,6,Y}
{5,3,1,2,6,Y}	{5,3,1,2,6,Y}	{5,4,1, 6,Y}
{5,4,1,2,6,Y}	{5,3,1,6,Y}	{5,4,1,2,6,Y}
{5,4,1,6,Y}	{5,3,1,6,Y}	{5,4,1,2,6,Y}
{5,3,1,6,Y}	{5,3,1,2,6,Y}	{5,4,1, 6,Y}