数据结构——循环队列

什么是循环队列

设计你的循环队列实现。
循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：
MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

---

实现的逻辑

在前面，我们实现队列是使用的链表，因为用链表实现，出队和入队的操作都很方便
所以在看到循环队列的时候，我们可能下意识得就会选择使用循环链表去实现，使其如果使用循环链表去实现会有一系列的问题，下面进行分析

用循环链表实现的不足

我们假设k为3，所以我们首先开辟3个节点，让front和rear都指向第一个节点

此时在队尾入队，每入一个，rear就指向下一个节点，直到满

可以发现，循环队列满的时候和空的时候的判断逻辑都是front==rear，所以就发生冲突，当front==rear时，无法判断队列到底是空的的还是满的。

为了解决这个问题，有2种办法：

1. 添加一个size变量，用于标识当前队列中元素个数
2. 增加一个额外的空节点

办法1可以解决问题，并且比较简单，这个就不做过多介绍

下面分析一下办法2，增加一个额外的空节点：
k的值仍然为4，因为增加一个空节点，所以要开辟5个节点

然后入队4次，此时队满

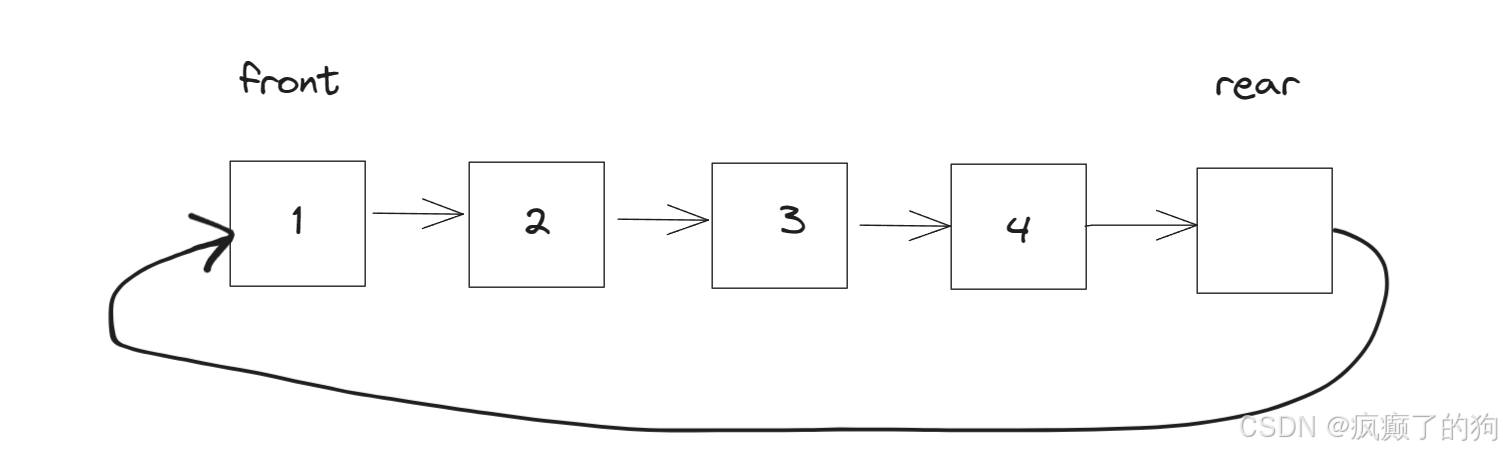
这里可以用rear->next==front用来判断队列是否满，这样就可以有效地去判断队列为空或者为满了

但是此时还有一个问题
我们要取队首元素时，可以用a[front]去取到值，但是想取队尾元素时发现，rear是指向队尾元素的下一个节点，所以想取到队尾元素，可以改写成双向循环链表或者再遍历一次，总之是不方便的。

所以，实现循环队列，使用数组实现更好。

用数组实现

循环队列用长度为k+1的数组实现

假设k为4，所以首先开辟大小为5的数组

同理，在rear入队，在front出队，每入队一个元素，向后走一位，每出队一个元素，front向后走一位。

队列满的时候：

此时，先出队一个元素，再入队一个元素，rear就应该变为0

所以就可以得出结论，入队的时候，如果rear不等于k的时候，正常+1就可以了，如果rear==k时，就需要变为0，所以这就实现了循环队列的效果

为了兼容这两种情况，rear的更新应该为：rear = (rear+1)%(k+1)
同理，front也会有这种情况，front = (front+1)%(k+1)

判断满的条件为：(rear+1)%(k+1)==front，因为队列满有2种情况：

所以，总结一下：

1. 用数组实现循环队列
2. 长度为k的循环队列，应该开辟长度为k+1的数组
3. front的更新公式：front = (front+1)%(k+1)，rear的更新公式：rear = (rear+1)%(k+1)
4. 判空条件：front == rear
5. 判满条件：(rear+1)%(k+1)==front
6. 取对头元素：a[front]
7. 取队尾元素：a[(rear+k)%(k+1)]

所以，根据上面的内容，对应的代码如下

---

代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct {
    int* data;
    int front;
    int rear;
    int k;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k);//构造器，设置队列长度为 k
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value);//向循环队列插入一个元素。如果成功插入则返回真
bool myCircularQueueDeQueue(MyCircularQueue* obj);//从循环队列中删除一个元素。如果成功删除则返回真
int myCircularQueueFront(MyCircularQueue* obj);//从队首获取元素。如果队列为空，返回 -1
int myCircularQueueRear(MyCircularQueue* obj);//获取队尾元素。如果队列为空，返回 -1
bool myCircularQueueIsEmpty(MyCircularQueue* obj);//检查循环队列是否为空
bool myCircularQueueIsFull(MyCircularQueue* obj);//检查循环队列是否已满
void myCircularQueueFree(MyCircularQueue* obj);//释放空间

bool CircularQueueIsEmpty(MyCircularQueue* obj)
{
    return obj->front == obj->rear;
}
bool CircularQueueIsFull(MyCircularQueue* obj) {
    if ((obj->rear + 1) % (obj->k + 1) == obj->front)
    {
        return true;
    }
    else
    {
        return false;
    }
}

MyCircularQueue* CircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    if (obj == NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    obj->front = obj->rear = 0;
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    if (obj->a == NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    obj->k = k;

    return obj;
}

bool CircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (myCircularQueueIsFull(obj))
        return false;
    else
    {
        obj->a[obj->rear] = value;
        obj->rear++;
        obj->rear %= (obj->k + 1);
        return true;
    }
}

bool CircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    else {
        obj->front++;
        obj->front %= (obj->k + 1);
        return true;
    }
}

int CircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
        return -1;
    else
    {
        return obj->a[obj->front];
    }
}

int CircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
        return -1;
    else
    {
        if (obj->rear == 0)
        {
            return obj->a[obj->k];
        }
        else {
            return obj->a[obj->rear - 1];
        }
    }
	//return obj->data[(obj->rear+obj->k)%(obj->k+1)];
}



void CircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    obj->a = NULL;
    free(obj);
    obj = NULL;
}