熵权法（EWM)

熵权法（Entropy Weight Method，EWM)

1. 介绍

熵值法又称熵权法，是最常用的客观求权重法之一，此类方法利用数据熵值信息即信息量大小进行权重计算，适用于数据之间有波动，同时将数据波动作为一种信息的情况，熵值法借鉴化学熵和信息熵的定义，通过定义各指标的熵值，将评估中各待评估单元信息进行量化和综合，得出各指标比较客观的权重。在数据中，离散程度越大，说明该指标对综合评价的影响越大，在信息论中，信息量越大，不确定性就越小，同时熵也就越小，反之信息量越小，不确定性就越大，熵就越大。

熵值法一般会涉及三个指标计算，分别是信息熵值、信息效用值以及权重系数

简单案例-相亲问题

小红毕业后参加相亲，现有表中5位候选人，她想从中挑出一位如意郎君，现请你帮她为年龄、身高、长相、学历、收入分配权重,进而求得最后总分，最高分者就是小红的结婚对象.

	年龄	身高	长相	学历(成绩)	收入
小明	24	180	60	90	5000
小A	23	175	90	85	10000
小B	23	170	95	92	8000
小C	24	185	81	100	5500
小D	25	190	79	60	2000

怎么求权重呢？

答：层次分析法 ，可以参考我之前写的博客 层次分析法（AHP）

可是小红同学是个选择困难症，认为这些标准很重要，而且想要权重避免主观.

客观赋值，就用熵权法

2. 原理

2.1 信息熵

熵是热力学的一个物理概念，是体系混乱度（或无序度）的量度。熵越大说明系统越混乱，携带的信息越少，熵越小说明系统越有序，携带的信息越多。

信息熵则借鉴了热力学中熵的概念 (注意：信息熵的符号与热力学熵应该是相反的[1])，用于描述平均而言事件信息量大小。所以数学上，信息熵其实是事件所包含的信息量的期望[2]。

在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。

根据上面期望的定义，我们可以设想信息熵的公式大概是这样的一个格式：

$$信息熵=\sum 每种可能事件的概率\ast 每种可能事件包含的信息量信息熵=\sum 每种可能事件的概率\ast 每种可能事件包含的信息量$$

基本思路是根据指标变异性的大小来确定客观权重。

规范点来说，设事件 $X$ 可能发生的情况分别为$:x_1,x_2,\cdot \cdot ,x_n.$定义事件$X$的信息熵为：

$$\begin{array}{c}H(X)=\sum _{i=1}^n[p(x_i)I(x_i)]=-\sum _{i=1}^n[p(x_i)\ln (p(x_i))]\end{array}$$

从这个公式可以看出，信息熵的本质就是对信息量的期望值。

为了方便，我们可以将这个离散函数当作连续函数$-x\ln x$ 讨论.由简单的数学知识可知$-{\lim }_{x\to 0}x\ln x=0$ ,将其求导可得到$-\ln x-1$,再次求导可得到$-\frac{1}{x}$,由此可知，这个函数有一个极大值点$x=\frac{1}{e}.$且二阶导不为0，所以极值点就是最值点，且唯一.那么类似的，$H(X)$也存在唯一的最大值，用拉格朗日乘数法可证得

$$\text{当且仅当}p\left(x_1\right)=p\left(x_2\right)=\cdot \cdot \cdot =p\left(x_n\right)=\frac{1}{n}\text{ 时, }H\left(X\right)\text{ 取最大值, 此时 }H\left(X\right)=\ln n.$$

一般来说，若某个指标的信息熵越小，表明指标值得变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，其权重也就越大。相反，某个指标的信息熵越大，表明指标值得变异程度越小，提供的信息量也越少，在综合评价中所起到的作用也越小，其权重也就越小。

💡个人理解：注意上面这段话，说的是提供的信息量，也就是已知的信息。提供的信息量越大，包含的信息也就越小。按照前面信息量的阐述，一个指标变异性越大则发生的概率越大，不确定也就越小，信息量也就越小，解决这个未知事物所需要的信息量也就越小，也就是说它本身提供了较多的信息量。

2.2 信息熵的定性分析

信息熵公式如下：

$$\begin{array}{c}H(X)=\sum _{i=1}^n[p(x_i)I(x_i)]=-\sum _{i=1}^n[p(x_i)\ln (p(x_i))].\end{array}$$

当且仅当$p\left(x_1\right)=p(x_2)=\cdots =p(x_n)=\frac{1}{n}$ 时，$H(X)$ 取最大值，此时 $H(X)=\ln n$.也就是说， 信息量的期望值最大，已掌握的信息量最少。

信息量的期望值最大，已掌握的信息量最少.

为什么呢？

直观的理解是，此时渣男和老实人出轨的概率均相等，也就是随机的均匀分布,此时要你据此判断面前这个人是不是渣男，那可不就是“盲猜”嘛。

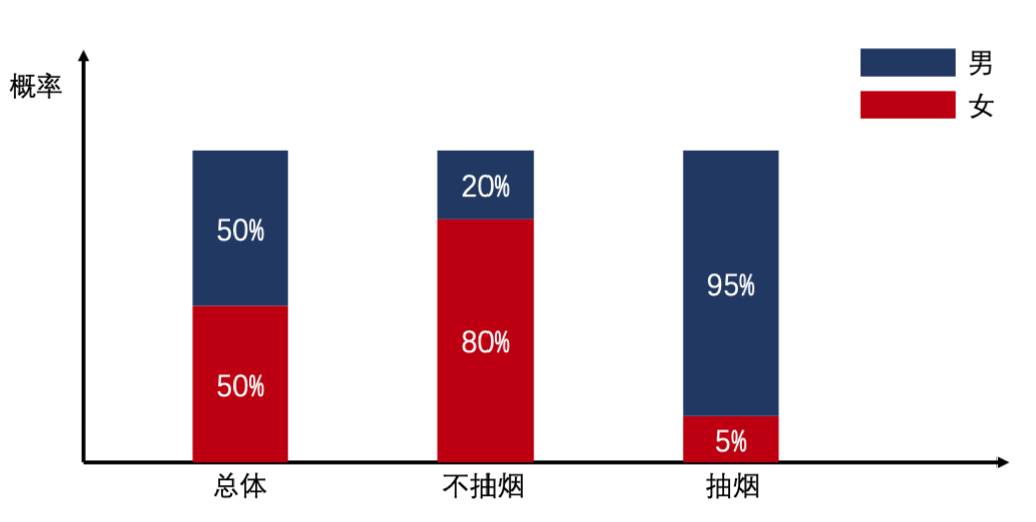
2.3 概率与信息量的关系

问题：一个渣男出轨和一个老实人出轨，,哪个瓜更好吃呢？

很明显是后者，因为渣男出轨的概率更大，一个安分守己的老实人出轨的概率更小，所以话题更“劲爆”，更颠覆我们的常识，此时这个信息告诉我们，“用出轨衡量渣男和老实男”的策略不靠谱。

概率$P(x)$越小，信息量$I(x)$越大，原先掌握的信息不靠谱。

概率$P(x)$越大，信息量$I(x)$越小，原先掌握的信息很靠谱。

所以定义$I(x)=-\ln (p(x))$。

基本思想信息熵小 → 得到的信息少，掌握的信息多 → 这组信息更靠谱 → 权重大.

掌握的是己有量，得到的是变量，变量少就是混乱程度小

3. 步骤

3.1 指标正向化

类型	特点	举例
极大型/效益型指标	数值越大越好	就业率、GDP、收入
极小型/成本型指标	数值越小越好	负债率、恩格尔系数
中间型指标	越接近某个值越好	黄金比例、满座率、水质pH值
区间型指标	落在某个区间最好	贫富差距、出生率

正向化的方法并不唯一，选择合适的即可，只要能转成极大型都可以

3.1.1 极小型正向化

极小型转极大型例如前面统计的失业率，这个数值应该是越小越好，所以可以用$\max -x$,或者$\frac{1}{x},(x>0)$

学校	失业率	正向化后的失业率
北大	0.010	0.030
清华	0.012	0.028
上交	0.040	0
浙大	0.033	0.007

3.1.2 中间型正向化

中间型转极大型数值不要太大也不要太小，越接近某个值越好，如$x_i$是一组中间型指标序列，且最佳的数值为$x_{\mathrm{best}}$, 那么可以这样正向化：

先取这个序列中最大差距值 M = max ⁡ { ∣ x i − x b e s t ∣ } M= \max \left \{ |x_i- x_{\mathrm{best}}|\right \} M=max{ ∣xi​−xbest​∣}, 再令各元素
$$\begin{array}{r}x\end{array}$$