1.5损失函数

思维引导

上一节你已经通过前向传播让网络输出了 “预测结果”（比如判断一张图是数字 3），但怎么知道这个预测 “准不准”？损失函数就是解决这个问题的 “误差尺子”—— 这一节会带你搞懂 “不同任务该用哪把尺子”（比如分类用交叉熵、回归用均方误差）、“尺子怎么量误差”（计算逻辑），以及在 Pytorch 里怎么用代码实现，这是后续 “通过反向传播调参” 的核心依据。

# 小节详细内容

1. 损失函数的定义：衡量误差的 “量化工具”

损失函数（Loss Function）的核心作用是 “计算网络预测结果与真实标签的差距”，输出的 “损失值”（Loss Value）是一个数字：

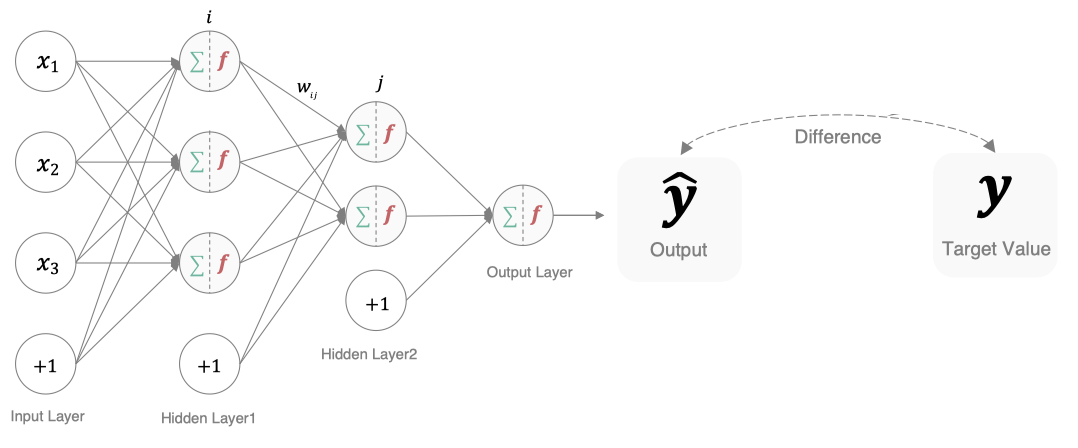
模型通过最小化损失函数的值来调整参数，使其输出更接近真实值。

• 损失值越小：说明预测结果和真实情况越接近（比如预测是 3，真实也是 3，损失值会很小）；

• 损失值越大：说明预测结果和真实情况差距越大（比如预测是 3，真实是 8，损失值会很大）。

  简单说，损失函数就是给网络的 “预测表现” 打分，分数越低越好，而后续的反向传播就是 “根据这个分数调整参数，争取下次考更高分”。

2. 常用损失函数：按任务类型分类（实战重点）

全连接网络主要用于 “分类任务”（如手写数字识别、图片分类）和 “回归任务”（如预测房价、气温），不同任务对应不同的损失函数，视频里重点讲了 2 种最常用的：

（1）交叉熵损失（Cross-Entropy Loss）：多分类任务专用

在多分类任务通常使用softmax（softmax是激活函数）将logits转换为概率的形式，所以多分类的交叉熵损失也叫做softmax损失，它的计算方法是：

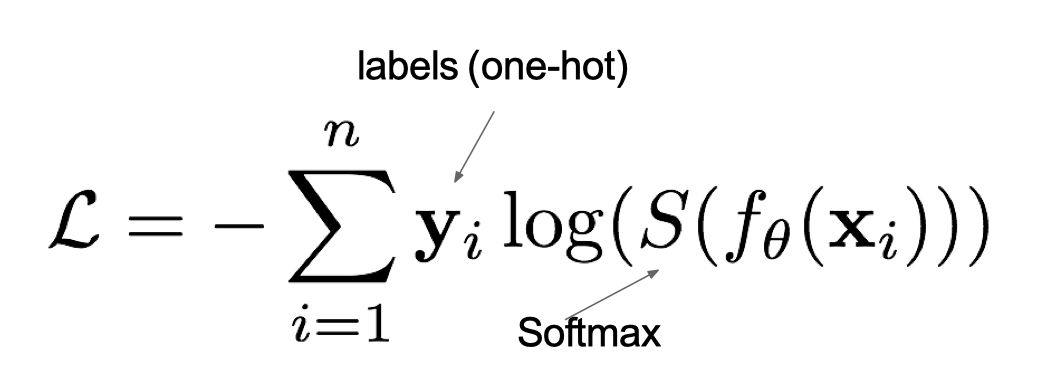
其中:

• $$y_i$$是样本x属于某一个类别的真实概率
• 而f(x)是样本属于某一类别的预测分数
• S是softmax激活函数，将属于某一类别的预测分数转换成概率
• L用来衡量真实值y和预测值f(x)之间差异性的损失结果

例子：

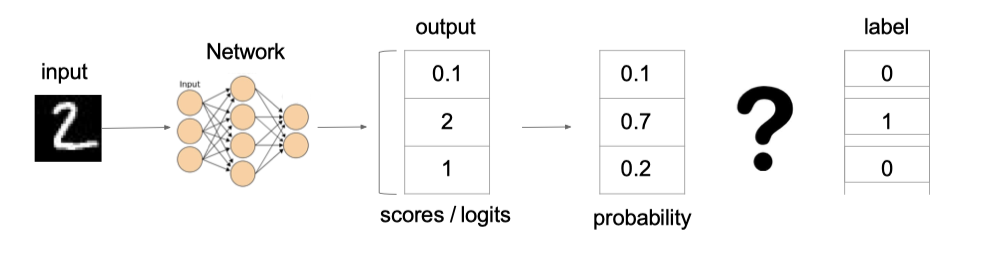
上图中的交叉熵损失为：

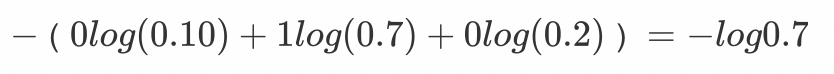
从概率角度理解，我们的目的是最小化正确类别所对应的预测概率的对数的负值(损失值最小)，如下图所示：

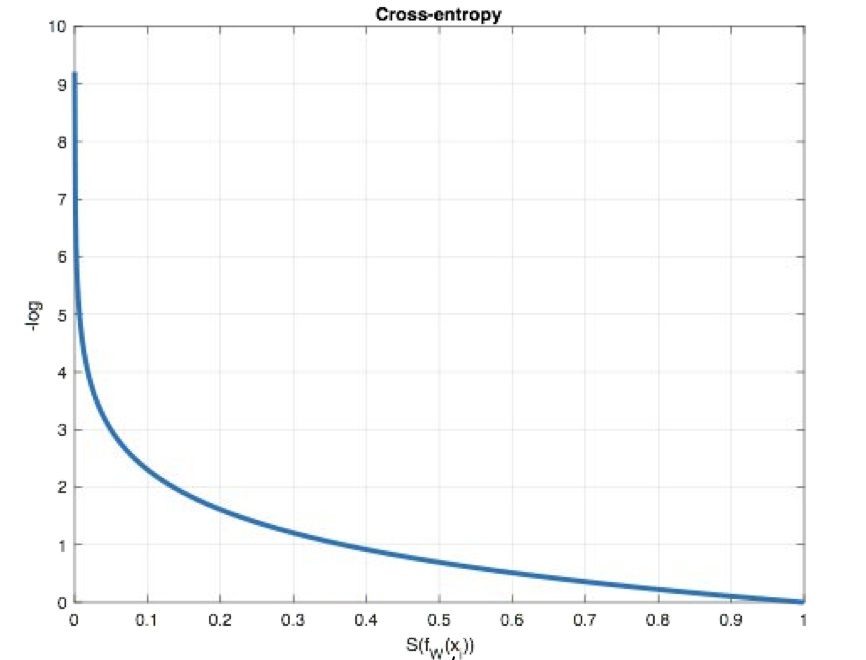
在PyTorch中使用nn.CrossEntropyLoss()实现，如下所示：

import torch
from torch import nn


# 分类损失函数：交叉熵损失使用nn.CrossEntropyLoss()实现。nn.CrossEntropyLoss()=softmax+损失计算
def test01():
	# 设置真实值: 可以是热编码后的结果也可以不进行热编码
	# y_true = torch.tensor([[0, 1, 0], [0, 0, 1]], dtype=torch.float32)
	# 注意：类型必须是64位整型数据
	y_true = torch.tensor([1, 2], dtype=torch.int64)
	y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], requires_grad=True, dtype=torch.float32)
	# 实例化交叉熵损失，默认求平均损失
	# reduction='sum'：总损失
	loss = nn.CrossEntropyLoss()
	# 计算损失结果
	my_loss = loss(y_pred, y_true).detach().numpy()
	print('loss:', my_loss)

(2)交叉熵损失（Cross-Entropy Loss）—二分类专用

在处理二分类任务时，我们不再使用softmax激活函数，而是使用sigmoid激活函数，那损失函数也相应的进行调整，使用二分类的交叉熵损失函数：

$$L=-y\log \hat{y}-(1-y)\log (1-\hat{y})$$

其中:

• y是样本x属于某一个类别的真实概率

• 而$$\hat{y}$$是样本属于某一类别的预测概率

  • L用来衡量真实值y与预测值$$\hat{y}$$之间差异性的损失结果。

  

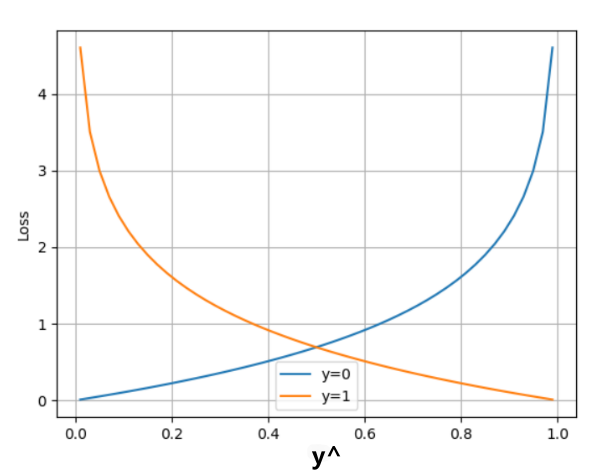
在PyTorch中实现时使用nn.BCELoss() 实现，如下所示：

import torch
from torch import nn


def test02():
    # 1 设置真实值和预测值
    y_true = torch.tensor([0, 1, 0], dtype=torch.float32)
    # 预测值是sigmoid输出的结果
    y_pred = torch.tensor([0.6901, 0.5459, 0.2469], requires_grad=True)
    # 2 实例化二分类交叉熵损失
    loss = nn.BCELoss()
    # 3 计算损失
    my_loss = loss(y_pred, y_true).detach().numpy()
    print('loss：', my_loss)

（3）均方误差损失（Mean Squared Error, MSE）：回归任务专用

• Mean Squared Loss/ Quadratic Loss(MSE loss)：也被称为L2 loss，或欧氏距离，它以误差的平方和的均值作为距离

• 适用场景：回归任务（预测连续值），比如预测房价（100 万、150 万）、预测气温（25℃、30℃）、预测股票价格等 —— 这些任务的 “真实标签” 不是离散的类别，而是连续的数字。

• 核心逻辑：通过 “预测值与真实值的平方差的平均值” 来计算损失，平方的作用是 “放大较大误差”（比如预测值和真实值差 10，平方后是 100；差 1，平方后是 1），让网络更关注大误差的样本。

• 公式：$$\text{MSE}=\frac{1}{N}\sum _{i=1}^N(y_i-{\hat{y}}_i{)}^2$$

函数图像：

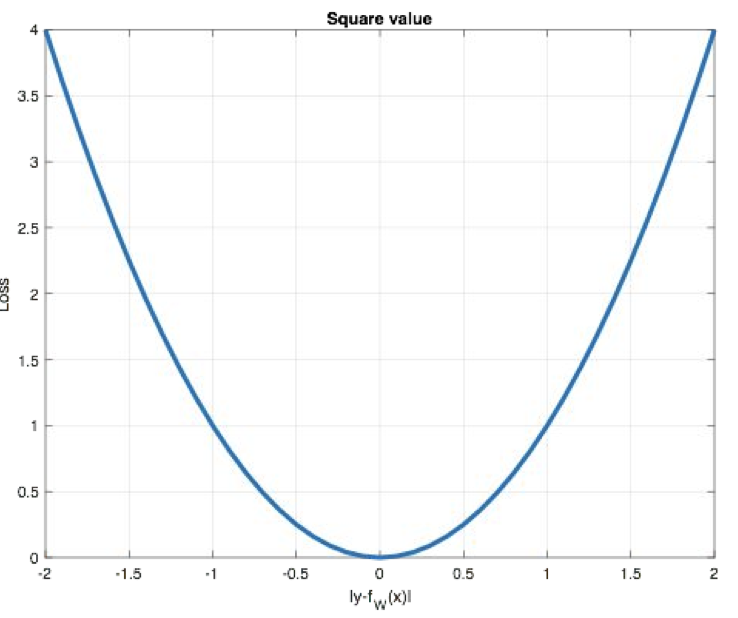
其中：

- yi​：第 i 个样本的真实值；
- y^​i​：第 i 个样本的预测值；
- n：样本总数。

特点是：

• L2 loss也常常作为正则项，对于离群点（outliers）敏感，因为平方项会放大大误差

• 当预测值与目标值相差很大时, 梯度容易爆炸

  • 梯度爆炸:网络层之间的梯度（值大于1.0）重复相乘导致的指数级增长会产生梯度爆炸

• 适用于大多数标准回归问题，如房价预测、温度预测等

• Pytorch 实现与示例：Pytorch 提供nn.MSELoss()类，使用时直接传入 “预测值” 和 “真实值” 即可，无需处理数据类型（默认torch.float）。

  • 代码示例（预测 “房屋面积→房价” 的回归任务）：

import torch
import torch.nn as nn

# 1. 定义回归用的全连接网络（输出层1个神经元，预测连续值）
class RegNet(nn.Module):
	def __init__(self):
		super(RegNet, self).__init__()
		self.fc1 = nn.Linear(1, 16)  # 输入层1个特征（房屋面积，如100㎡）
		self.fc2 = nn.Linear(16, 1)   # 输出层1个值（预测房价，如120万）
		self.relu = nn.ReLU()
	
	def forward(self, x):
		x = self.fc1(x)
		x = self.relu(x)
		x = self.fc2(x)
		return x

# 2. 创建网络、损失函数实例
net = RegNet()
criterion = nn.MSELoss()  # 初始化均方误差损失

# 3. 模拟数据：输入（房屋面积）+ 真实标签（房价）
input_area = torch.tensor([[100.0], [120.0]], dtype=torch.float)  # 2个样本，面积100㎡、120㎡
true_price = torch.tensor([[120.0], [150.0]], dtype=torch.float)  # 真实房价120万、150万

# 4. 计算损失
outputs = net(input_area)  # 网络输出预测房价，维度(2,1)
loss = criterion(outputs, true_price)  # 计算MSE损失
print("MSE损失值：", loss.item())  # 输出示例：500.0（初始参数随机，损失值可能较大，合理）

（4）MAE损失函数

**mean absolute loss(MAE)**也被称为L1 Loss，是以绝对误差作为距离

损失函数公式:

$$\text{MAE}=\frac{1}{N}\sum _{i=1}^N\left|y_i-{\hat{y}}_i\right|$$

曲线如下图所示：

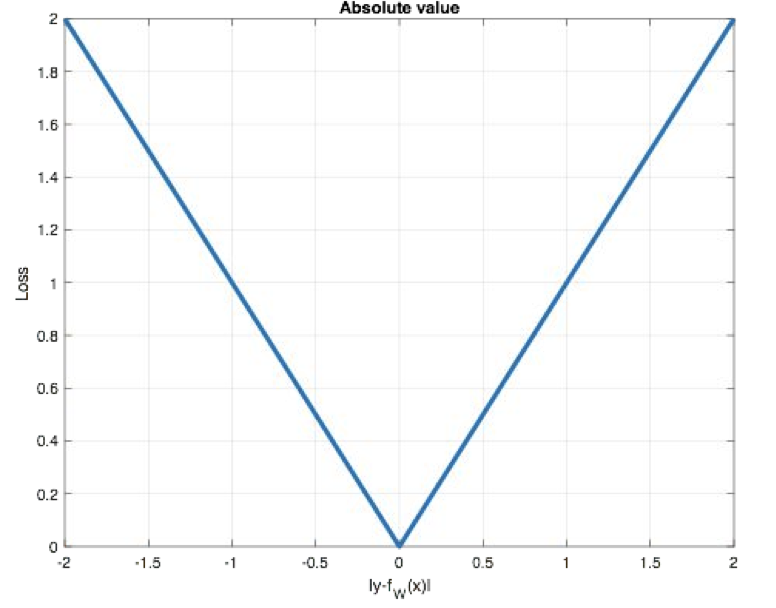
特点是：

• 由于L1 loss具有稀疏性，为了惩罚较大的值，因此常常将其作为正则项添加到其他loss中作为约束。(0点不可导, 产生稀疏矩阵)
• L1 loss的最大问题是梯度在零点不平滑，导致会跳过极小值
• 适用于回归问题中存在异常值或噪声数据时，可以减少对离群点的敏感性

在PyTorch中使用nn.L1Loss()实现，如下所示：

import torch
from torch import nn


# 计算inputs与target之差的绝对值
def test03():
    # 1 设置真实值和预测值
    y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
    y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)
    # 2 实例MAE损失对象
    loss = nn.L1Loss()
    # 3 计算损失
    my_loss = loss(y_pred, y_true).detach().numpy()
    print('loss:', my_loss)

（5）Smooth L1损失函数

smooth L1说的是光滑之后的L1，是一种结合了均方误差（MSE）和平均绝对误差（MAE）优点的损失函数。它在误差较小时表现得像 MSE，在误差较大时则更像 MAE。

Smooth L1损失函数如下式所示：

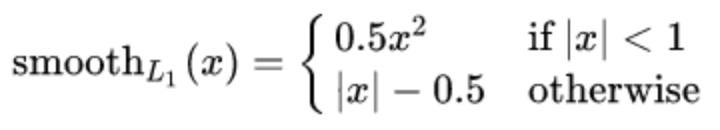
其中：𝑥=f(x)−y 为真实值和预测值的差值。

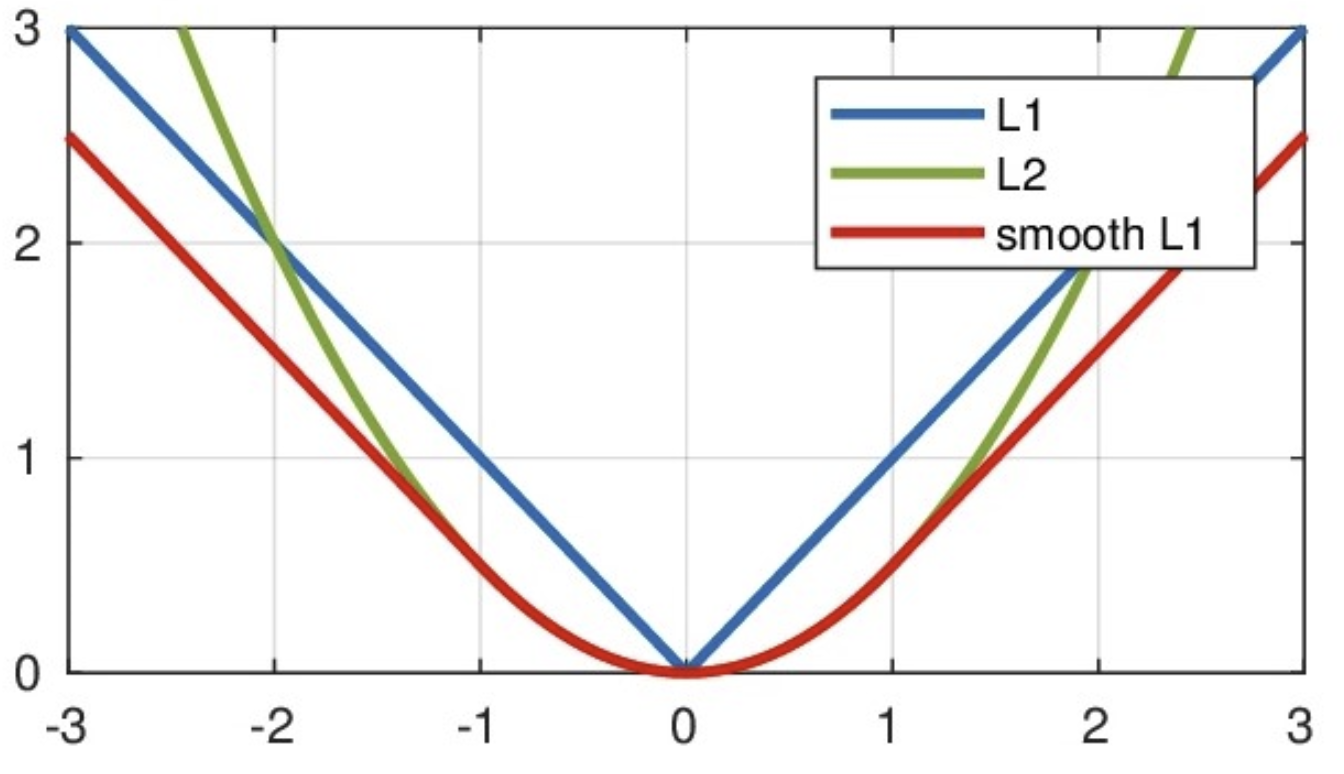
从上图中可以看出，该函数实际上就是一个分段函数

• 在[-1,1]之间实际上就是L2损失，这样解决了L1的不光滑问题
• 在[-1,1]区间外，实际上就是L1损失，这样就解决了离群点梯度爆炸的问题

特点是：

• 对离群点更加鲁棒：当误差较大时，损失函数会线性增加（而不是像MSE那样平方增加），因此它对离群点的惩罚更小，避免了MSE对离群点过度敏感的问题

• 计算梯度时更加平滑：与MAE相比，Smooth L1在小误差时表现得像MSE，避免了在训练过程中因使用绝对误差而导致的梯度不连续问题

在PyTorch中使用nn.SmoothL1Loss()计算该损失，如下所示：

import torch
from torch import nn


def test05():
    # 1 设置真实值和预测值
    y_true = torch.tensor([0, 3])
    y_pred = torch.tensor([0.6, 0.4], requires_grad=True)
    # 2 实例smmothL1损失对象
    loss = nn.SmoothL1Loss()
    # 3 计算损失
    my_loss = loss(y_pred, y_true).detach().numpy()
    print('loss:', my_loss)

3. 损失值的 “合理范围” 与注意事项

• 没有 “固定标准”：损失值的大小取决于任务和数据（比如分类任务初始损失约 2-3，回归任务可能从几百到几万不等），关键看 “训练过程中损失值是否持续下降”—— 只要损失在逐步降低，说明网络在学习；如果损失不下降甚至上升，说明训练有问题（如参数初始化错、学习率太高）。
• 避免 “只看损失值”：损失小不代表模型 “好用”，比如分类任务损失很小，但在新样本上预测不准（过拟合），这时候需要结合 “准确率” 等指标判断；回归任务则要结合 “真实场景的误差可接受范围”（比如预测房价误差 5 万以内可接受，即使损失值还有 10）。