LeetCode题练习与总结：四叉树交集--558

一、题目描述

二进制矩阵中的所有元素不是 0 就是 1 。

给你两个四叉树，quadTree1 和 quadTree2。其中 quadTree1 表示一个 n * n 二进制矩阵，而 quadTree2 表示另一个 n * n 二进制矩阵。

请你返回一个表示 n * n 二进制矩阵的四叉树，它是 quadTree1 和 quadTree2 所表示的两个二进制矩阵进行 按位逻辑或运算 的结果。

注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 接受 。

四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

• val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
• isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

我们可以按以下步骤为二维区域构建四叉树：

1. 如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
2. 如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
3. 使用适当的子网格递归每个子节点。

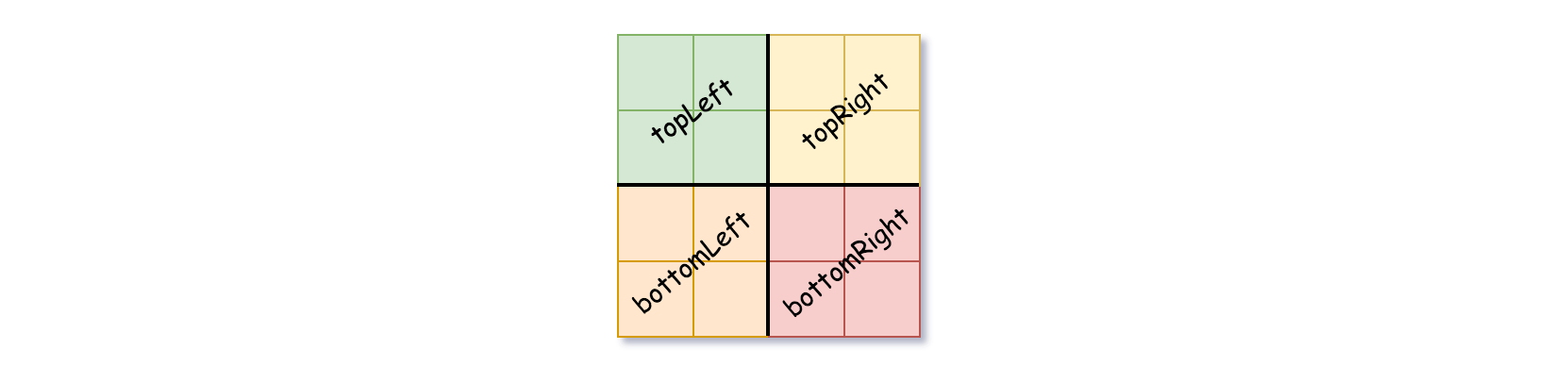
如果你想了解更多关于四叉树的内容，可以参考 百科。

四叉树格式：

输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。

它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。

如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 0 。

示例 1：

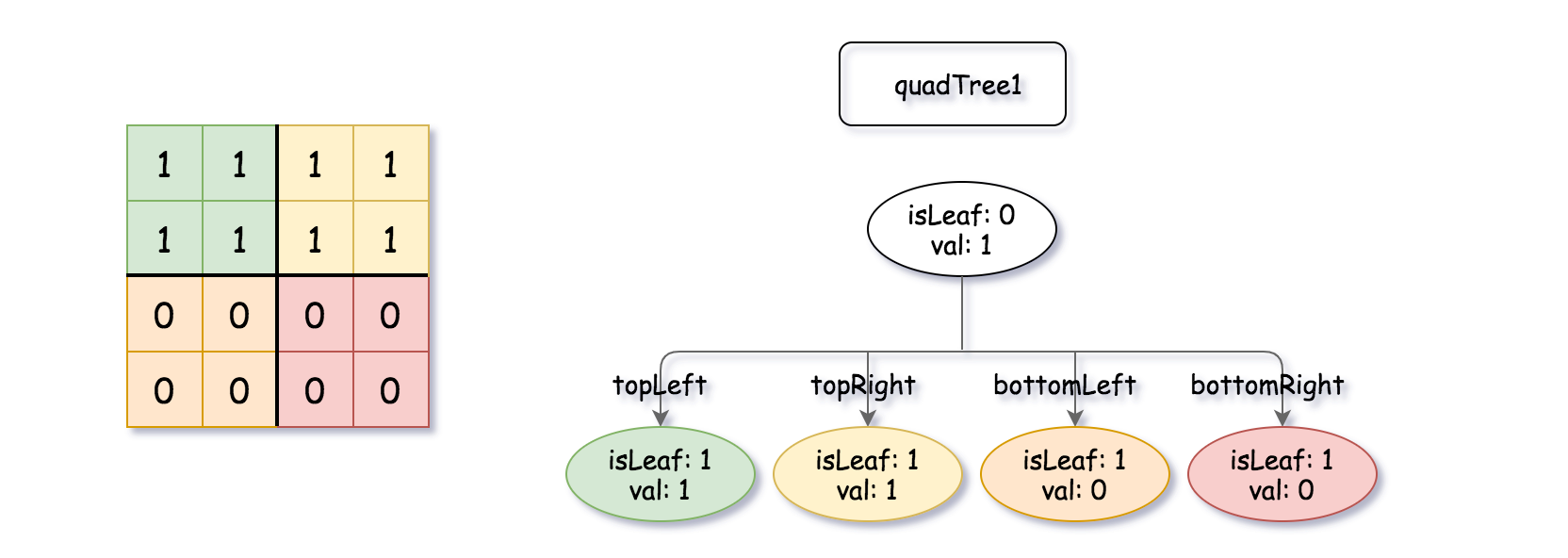
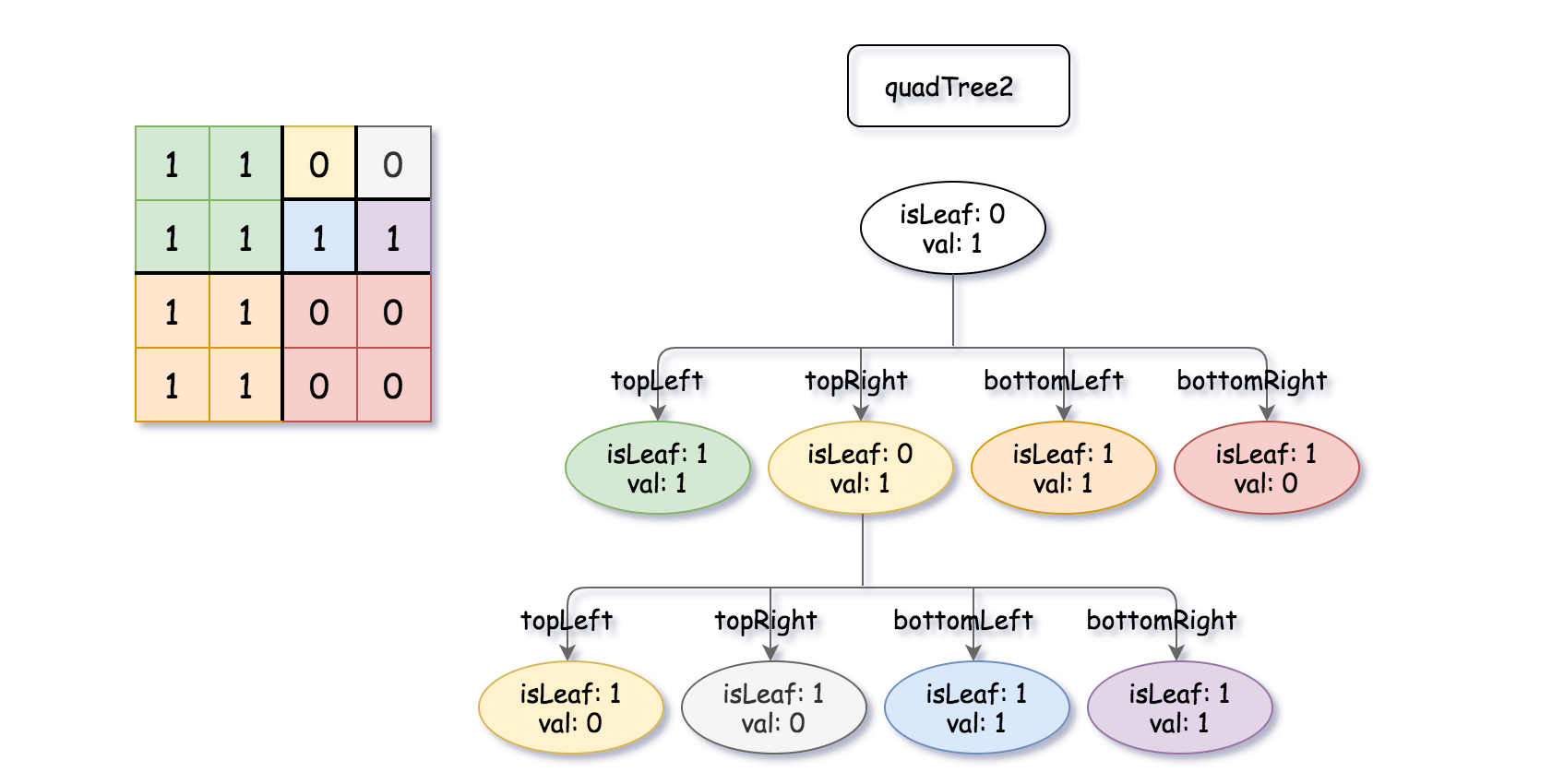
输入：quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
输出：[[0,0],[1,1],[1,1],[1,1],[1,0]]
解释：quadTree1 和 quadTree2 如上所示。由四叉树所表示的二进制矩阵也已经给出。
如果我们对这两个矩阵进行按位逻辑或运算，则可以得到下面的二进制矩阵，由一个作为结果的四叉树表示。
注意，我们展示的二进制矩阵仅仅是为了更好地说明题意，你无需构造二进制矩阵来获得结果四叉树。

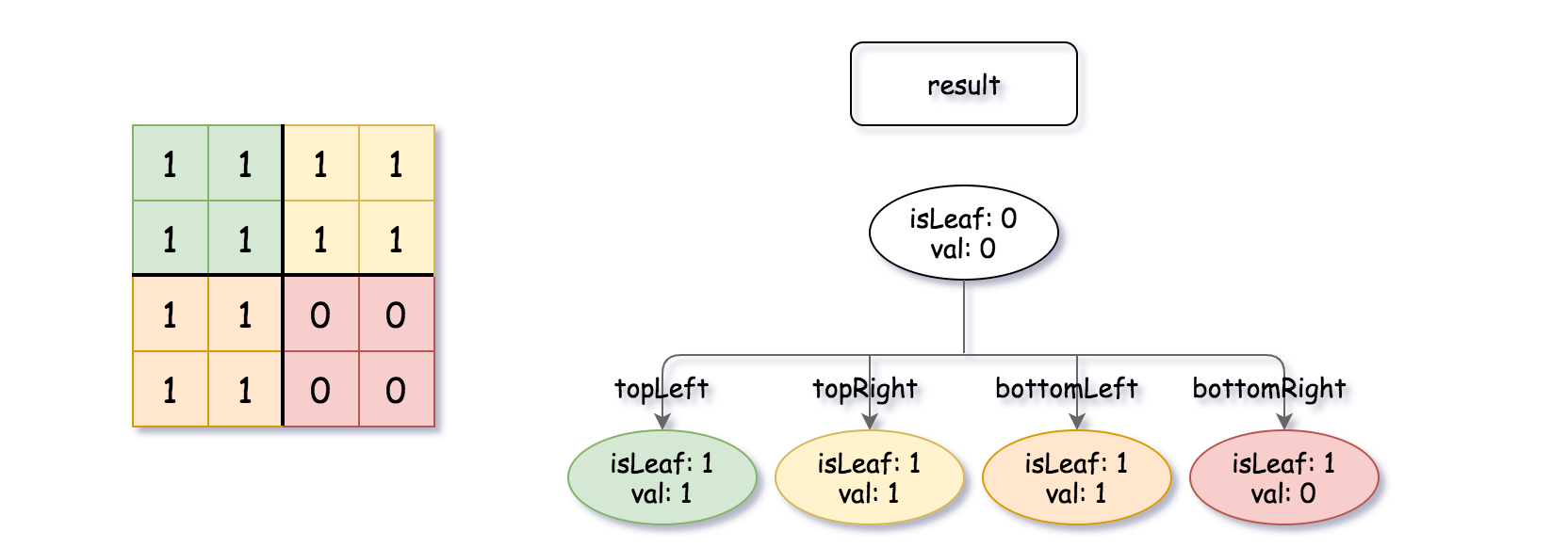
示例 2：

输入：quadTree1 = [[1,0]]
, quadTree2 = [[1,0]]
输出：[[1,0]]
解释：两个数所表示的矩阵大小都为 1*1，值全为 0 
结果矩阵大小为 1*1，值全为 0 。

提示：

• quadTree1 和 quadTree2 都是符合题目要求的四叉树，每个都代表一个 n * n 的矩阵。
• n == 2^x ，其中 0 <= x <= 9.

二、解题思路

1. 如果quadTree1是叶子节点，并且其值为1，那么直接返回quadTree1，因为1或任何数都是1。
2. 如果quadTree1是叶子节点，并且其值为0，那么返回quadTree2，因为0或任何数都是那个数本身。
3. 如果quadTree2是叶子节点，并且其值为1，那么直接返回quadTree2，因为理由同步骤1。
4. 如果quadTree2是叶子节点，并且其值为0，那么返回quadTree1，因为理由同步骤2。
5. 如果quadTree1和quadTree2都不是叶子节点，那么递归地对它们的四个子节点进行按位或运算，并更新当前节点的子节点。
6. 在递归之后，检查四个子节点是否都是叶子节点，并且它们的值都相同。如果是，那么当前节点可以变成叶子节点，其值为子节点的值。

三、具体代码

class Solution {
    public Node intersect(Node quadTree1, Node quadTree2) {
        // 如果quadTree1是叶子节点且值为1，直接返回quadTree1
        if (quadTree1.isLeaf) {
            return quadTree1.val ? quadTree1 : quadTree2;
        }
        // 如果quadTree2是叶子节点且值为1，直接返回quadTree2
        if (quadTree2.isLeaf) {
            return quadTree2.val ? quadTree2 : quadTree1;
        }
        
        // 递归处理四个子节点
        quadTree1.topLeft = intersect(quadTree1.topLeft, quadTree2.topLeft);
        quadTree1.topRight = intersect(quadTree1.topRight, quadTree2.topRight);
        quadTree1.bottomLeft = intersect(quadTree1.bottomLeft, quadTree2.bottomLeft);
        quadTree1.bottomRight = intersect(quadTree1.bottomRight, quadTree2.bottomRight);
        
        // 检查四个子节点是否都是叶子节点且值相同
        if (quadTree1.topLeft.isLeaf && quadTree1.topRight.isLeaf &&
            quadTree1.bottomLeft.isLeaf && quadTree1.bottomRight.isLeaf &&
            quadTree1.topLeft.val == quadTree1.topRight.val &&
            quadTree1.topLeft.val == quadTree1.bottomLeft.val &&
            quadTree1.topLeft.val == quadTree1.bottomRight.val) {
            // 如果是，当前节点变成叶子节点，值为子节点的值
            quadTree1.isLeaf = true;
            quadTree1.val = quadTree1.topLeft.val;
        }
        
        return quadTree1;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

• 在最坏的情况下，我们需要遍历两个四叉树的所有节点。对于每个节点，我们可能会进行一次递归调用，除非当前节点是叶子节点并且其值为1或者另一个树也是叶子节点且其值为1，这种情况下我们不需要递归。

• 四叉树的大小是 n×n，其中 n = 2^x，x 的范围是 0≤x≤9。因此，四叉树的大小最多是 512×512。

• 每个节点最多会被访问一次，并且对于每个节点，我们可能会递归地访问其四个子节点。

• 因此，时间复杂度是 O(N)，其中 N 是两个四叉树中节点的总数。在最坏的情况下，N 最多是 4×512×512。

2. 空间复杂度

• 递归调用的深度取决于四叉树的高度。由于四叉树的大小是 n×n，其高度最多是 log2​(n)。

• 递归调用的空间复杂度是递归调用的最大深度，即四叉树的高度。因此，空间复杂度是 O(logN)，其中 N 是四叉树的大小。

• 在递归调用过程中，我们没有使用额外的空间来存储中间结果，除了递归调用栈。

• 因此，空间复杂度是 O(logN)，其中 N 是四叉树的大小。

五、总结知识点

• 递归算法：

  • 代码通过递归的方式处理四叉树节点的合并。递归是一种常用的算法设计方法，它通过函数自身调用自身来简化问题的处理。

• 四叉树数据结构：

  • 四叉树是一种树形数据结构，每个节点有四个子节点：topLeft、topRight、bottomLeft、bottomRight。
  • 四叉树通常用于分割二维空间，常用于图像处理、地理信息系统等领域。

• 逻辑运算：

  • 代码中使用了逻辑与（&&）和逻辑或（||）运算符来检查条件。
  • 三元运算符（?:）用于简洁地表达条件赋值。

• 布尔类型和布尔逻辑：

  • 代码中的 isLeaf 属性是一个布尔类型，表示节点是否是叶子节点。
  • val 属性也是一个布尔类型，表示叶子节点的值。

• 对象引用：

  • 在递归调用中，通过引用传递四叉树的子节点，这意味着函数内部对节点的修改会影响到原始的四叉树结构。

• 条件判断：

  • 代码中包含多个 if 语句，用于根据节点是否是叶子节点以及叶子节点的值来决定递归的终止条件以及如何合并节点。

• 短路逻辑：

  • 在条件判断中使用短路逻辑，例如，如果 quadTree1.isLeaf 为 true，则不会检查 quadTree2.isLeaf。

• 代码复用：

  • 递归函数 intersect 被设计为通用的，可以处理任意两个四叉树的合并，体现了代码的复用性。

• 内存管理：

  • 在递归过程中，不需要额外的内存空间来存储中间结果，因为节点的修改是就地进行的，这有助于减少内存使用。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。