目录
1,求积分
1,梯形法求积分trapz
列出一组(x,y)对应值
trapz(x,y)
2,integral
q = integral(fun,xmin,xmax) 使用全局自适应积分和默认误差容限在 xmin 至 xmax 间以数值形式为函数 fun 求积分。
3,,integral2对二重积分进行数值计算
求下列积分的数值解
(1)
clc,clear;
fun=@(x)1/sqrt(2*pi)*exp(-x.^2/2);
integral(fun,0,1)(6)
clc,clear;
fun=@(r,th)sqrt(1+r.^2.*sin(th));
integral2(fun,0,1,0,2*pi)(7)
clear;clc;
fun = @(x,y) 1+x+y.^2;
//需要手动算一下上下限
ymin = @(x)-sqrt(2*x-x.^2);
ymax = @(x)sqrt(2*x-x.^2);
integral2(fun,0,2,ymin,ymax)2,坡度gradient
gradient(y,x)
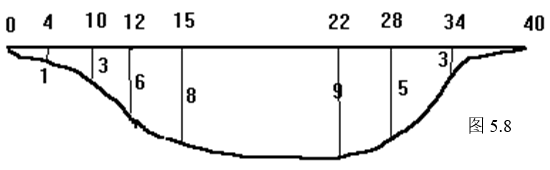
1. 某河床的横断面如图5.8所示,为了计算最大的排洪量,需要计算它的断面积,试根据图示测量数据(单位:米)用梯形法计算其断面积。
2. 求图5.8各测量点的坡度。
x=[0 4 10 12 15 22 28 34 40];
y=[0 1 3 6 8 9 5 3 0];
trapz(x,y)
gradient(y,x)2,求导
已知参数方程
试取t的步长0.01, 求
的数值解。
t=0:0.01:1.5;
x=log(cos(t));
y=cos(t)-t.*sin(t);
dydx=gradient(y,x) %这里dydx仅仅是个普通变量名
plot(x,dydx) %dydx函数图,作图观察x=-1时,dydx的值约0.9
%以下是更精确的编程计算方法
[x_1,id]=min(abs(x-(-1)));%找最接近x=-1的点,id为这个点的下标
dydx(id)





 本文探讨了数值积分的梯形法则(trapezoidal rule)应用,包括一维函数`fun`的积分计算、二重积分`integral2`实例,以及利用`gradient`求解坡度。内容涉及自适应积分`integral`、特定函数的数值解和曲线导数的计算。
本文探讨了数值积分的梯形法则(trapezoidal rule)应用,包括一维函数`fun`的积分计算、二重积分`integral2`实例,以及利用`gradient`求解坡度。内容涉及自适应积分`integral`、特定函数的数值解和曲线导数的计算。
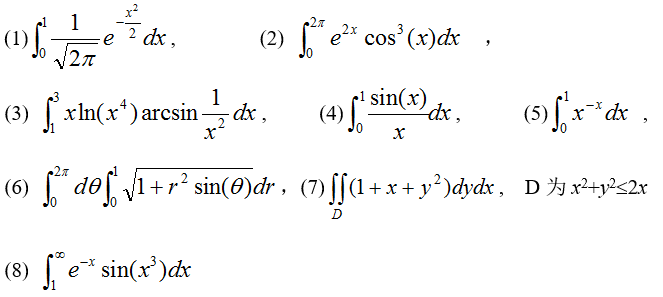
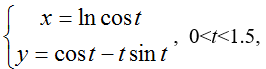
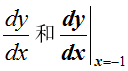
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








