目录
rref-------简化的行阶梯形矩阵(Gauss-Jordan 消去法)
设a=(1,2,3),b=(2,4,3), 分别计算a./b, a.\b, a/b, a\b, 分析结果的意义。
1,对应元素分别运算a除以b
2,对应元素分别运算b除以a
3,A/B是A乘B的逆矩阵的意思 (/x=乘以x的逆)
4,B\A是B的逆矩阵乘A的意思。(x\=x的逆乘以)
1,解方程组
2. 用矩阵除法解下列线性方程组,并判断解的意义,用矩阵乘法验算。
rank 函数判定解的情况
1)当方程组的系数矩阵的秩与方程组增广矩阵的秩相等且均等于方程组中未知数个数n的时候,方程组有唯一解
2)当方程组的系数矩阵的秩与方程组增广矩阵的秩相等且均小于方程组中未知数个数n的时候,方程组有无穷多解
3)当方程组的系数矩阵的秩小于方程组增广矩阵的秩的时候,方程组无解
NULL
z=null(a) {返回 A 的零空间的标准正交基}
>>a矩阵*x=0
>>解x
rref-------简化的行阶梯形矩阵(Gauss-Jordan 消去法)
用途为解方程组
(1)唯一解
>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];
>> rank(A), rank([A,b])
//[A,b]为增广矩阵, 求rank的目的是为了判断解的意义,注意不要写成rank(A,b)。
ans =
3
ans =
3
//可见方程组唯一解
>> x=A\b
x =
2.3830
1.4894
2.0213(2)唯一解
>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];
>> rank(A), rank([A,b])
ans =
3
ans =
3 %可见方程组唯一解
>> x=A\b
x =
-0.4706
-0.2941
0(3)无解
>> A=[4 1;3 2;1 -5];b=[1;1;1];
>> rank(A), rank([A,b])
ans =
2
ans =
3 %可见方程组无解
>> x=A\b
x =
0.3311
-0.1219 %最小二乘近似解(4) 求通解
clear;clc
a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法
ra=rank(a),rab=rank([a,b])
%结果:
ra = 3
rab = 3
%ra==rab<4说明有无穷多解
x0=a\b
%结果:
x0 =
1
0
1
0
%x0是一个特解
v=null(a)
%结果:
v =
-0.6255
0.6255
-0.2085
0.4170
%{v}为齐次方程ax=0的基础解系,从而x=cv+x0(c为任意常数)为方程的通解使用rref求解:
>> rref([a,b])
ans =
1.0000 0 0 1.5000 1.0000
0 1.0000 0 -1.5000 0
0 0 1.0000 0.5000 1.0000
%前4列分别对应x1-x4, 通解x=k*[-1.5,1.5,-0.5,1]'+[1,0,1,0]'4. (人口流动趋势) 对城乡人口流动作年度调查,发现有一个稳定的朝向城镇流动的趋势,每年农村居民的5%移居城镇而城镇居民的1%迁出,现在总人口的20%位于城镇。假如城乡总人口保持不变,并且人口流动的这种趋势继续下去,那么
(1) 一年以后住在城镇人口所占比例是多少?两年以后呢?十年以后呢?
(2) 很多年以后呢?
(3) 如果现在总人口70%位于城镇,很多年以后城镇人口所占比例是多少?
(4) 计算转移矩阵的最大特征值及对应的特征向量,与问题(2)(3)有何关系?
clc,clear
city=0.2;country=0.8;
y=10;
for i=1:y
if i==1 | i==2 |i==10
i
city=city*0.99+country*0.05
country=country*0.95+city*0.01
end
end
很多年之后
city=0.2;country=0.8;
t=0;
y=100000
for i=1:y
if country==country*0.95+city*0.01
break
else
i,
city=city*0.99+country*0.05,
country=country*0.95+city*0.01
end
end
i =
584
city =
0.8387
country =
0.1677
(3)如果现在总人口70%位于城镇,很多年以后城镇人口所占比例是多少?
(稍作改良)
city=0.7;country=0.3;
t=0;
y=100000
for i=1:y
if country-country*0.95+city*0.01<=1e-6
break
else
i,
city=city*0.99+country*0.05,
country=country*0.95+city*0.01
end
end
(4) 特征值与特征向量
[V,D]= eig(A) 返回特征值的对角矩阵 D 和矩阵 V,其列是对应的右特征向量,使得 A*V = V*D。
//(4) 计算转移矩阵的最大特征值及对应的特征向量,与问题(2)(3)有何关系?
x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];
x=x0;for i=1:1000,x=a*x;end,x
x =
0.8333
0.1667>> [v,e]=eig(a)
v =
0.9806 -0.7071
0.1961 0.7071
e =
1.0000 0
0 0.9400
>> v(:,1)./x
ans =
1.1767
1.1767
%v(:,1)与x成比例,说明x也是最大特征值1对应的特征向量








 本文探讨了通过rank函数判定线性方程组解的情况,包括唯一解、无穷解和无解,并利用rref方法求解和特征值特征向量的应用。还结合实际问题如城乡人口流动趋势进行了分析。
本文探讨了通过rank函数判定线性方程组解的情况,包括唯一解、无穷解和无解,并利用rref方法求解和特征值特征向量的应用。还结合实际问题如城乡人口流动趋势进行了分析。
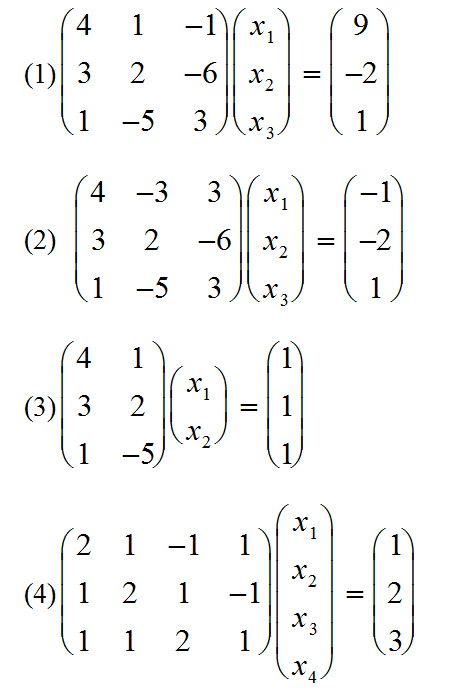
















 6566
6566

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








