算法特论学习笔记(3)

学习目标：

 回归分析

首先是，单回归分析。

 

 

 回归分析是对数据进行函数拟合的方法，一元回归分析是利用一个解释变量预测一个目的变量的回归分析方法，上面的例子是目的变数𝑦体重,解释变数𝑥身高，除了身高和体重的关系，还有租房面积和房租的关系。目的变量和解释变量成线性比例的关系，也被称为直线回归。

比如，𝑦=𝜔0+𝜔1𝑥y=ω0+ω1 xとしたとき𝜔0と𝜔1は以下のように求める。

  

この式は一般的に各目的変数における残差（誤差）の二乗和𝐸Eが最小になるよう求める。

 𝜔0と𝜔1それぞれについて偏微分を用いて連立方程式を作り，𝜔0と𝜔1を決定，

 𝜔0ω_0と𝜔1ω_1をそれぞれに変化させ誤差が最小になる点を求める。

 

 

接下来是，多元回归分析

 用多个解释变量预测一个目的变量的方法，一元回归分析用一个解释变量预测一个目的变量。

 

 多元回归分析之一，是用一个解释变量的多项式预测一个目的变量的方法，用曲线拟合数据。

 

一元回归分析中，回归方程是线性函数，所以说明变量的阶数为1，但数据为直线拟合。

 

接下来是逻辑回归，

 比如以现象的发生概率为目的变量，组合多个解释变量，通过回归求得的方法，火烈胶通过逻辑回归发现，冠心病的风险因素包括年龄、胆固醇、吸烟等。

 

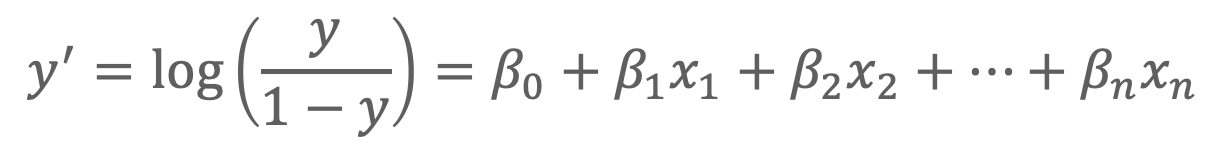
 y‘的这个变换被称为rosit变换，即取0 ~ 1的值为−∞~∞

不能计算变换前的值是0和1的情况是弱点，在这种情况下，可以使用无限接近0或1的值来代替
ロジット变换ロジスティック函数y = 1 /(1 -𝑒^(碟-𝑦〗^消息))的逆函数，𝑦^消息进行了重回归分析后,使用ロジスティック函数𝑦推定的辨别成绩。

 在逻辑回归的判断中使用判断得分，推测出的判断得分与判断准确率之间存在相关关系，判断得分大于0.5→发生现象，判断得分小于0.5→没有现象发生。

多项式回归中解释变量的阶数，

 多项式回归是用一个解释变量的多项式来预测一个目的变量的方法，

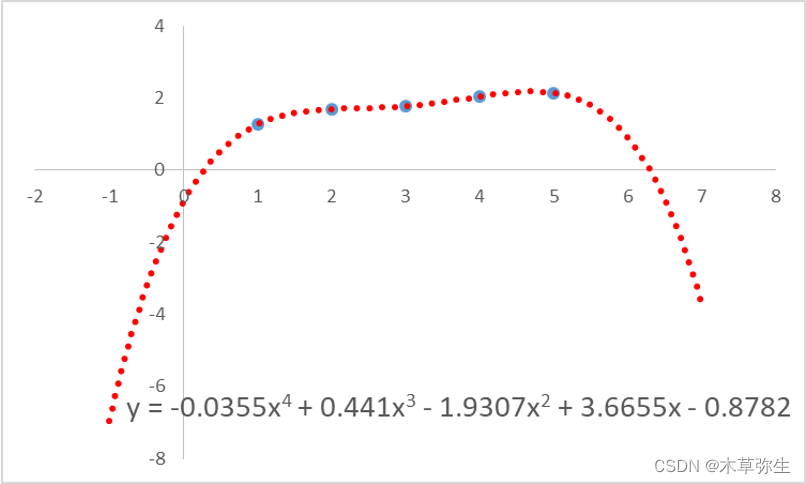
 如果阶数超过2，曲线也可以回归，提高阶数会产生什么样的曲线?如果我们提高阶数，我们可以让回归的残差接近于零。但是对未知数据的预测误差会变大。

 

 

 

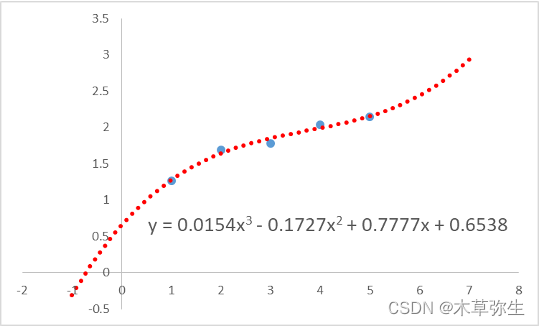
 这个问题被称为过度拟合，在进行回归分析时，尽可能使用阶数小的模型，避免过度拟合 。

 

 多元回归分析是利用多个解释变量预测一个目的变量的方法，

  解释变量的数量越多，回归误差越小，在预测体重时，不要只看身高，还要把胸围、脚的尺寸、性别等作为说明变量，这样才能提高预测的精度，但是，如果增加解释变量，就容易出现多路共线的问题。多重共线性:说明变量之间的关联性变高，回归变得不稳定。

 

因此，如果增加解释变量，就无法得出回归的解。在社会学领域的调查和生命医学领域的测量数据中。我们可以通过Lasso回归方法来避免，Lasso从相关度高的解释变量中选出一个来进行回归。

接下来是正规化

 回归分析中避免过度拟合的方法，过剩发生匹配的解释变量𝜔值合计增大的情况。

  为了防止过剩匹配𝜔解释变数的值的比值小的，误差不仅说明𝜔变数的值合计变小一样计算。