操作符中的重难点（2）

最新推荐文章于 2023-03-20 20:35:31 发布

pengzhenliao

最新推荐文章于 2023-03-20 20:35:31 发布

阅读量502

点赞数 5

文章标签： c语言开发语言后端

本文链接：https://blog.youkuaiyun.com/weixin_60498596/article/details/121341313

版权

1.单目操作符

这里我们重点介绍一下前置，后置++和前置，后置--。

前置，后置++是怎么计算的呢？它的计算规则是先++后使用，后置++是先使用后++。

前置，后置--是怎么样计算的呢？它的计算规则是先--后使用，后置--是先使用后--。

我们用代码来演示一下。

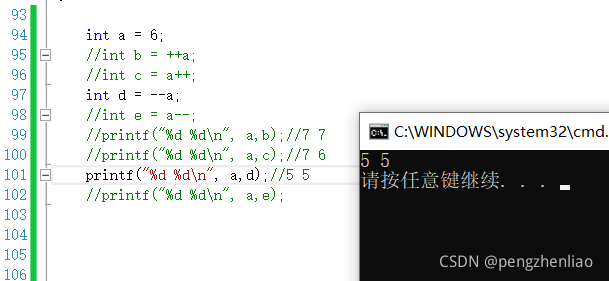
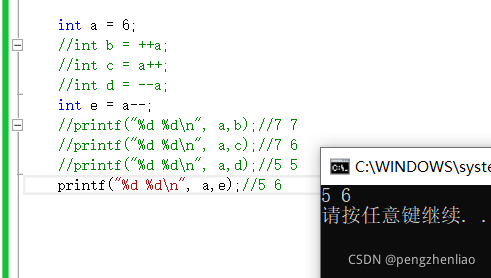
这必须要注意！！！

接下来看看这个例子：

这个例子的题目在vs中得到的是12，4，在gcc中却得到的是10，4，这是为什么呢？

这是编译器对计算优先级不同而得到了不同的结果，这种代码还是尽量避免。

接下来在看看这个单目操作符（类型）--强制类型转换。看看这个代码

虽然编译成功了，但是这里会报警告，我们可以这样来解决。

这里用（int）来进行强制类型转换，只会取整数部分。但是不建议经常用。

2.sizeof和数组

sizeof是求数组所占空间的操作符我们来看看它有哪些需要注意的点。

来看看以下代码。

sizeof（）内部单独放一个数组名，数组名表示整个数组，前面得到的是40和10。

我们知道数组传参传的是首元素的地址，形参接收时是一个指针变量，所以在函数内部sizeof（）算出来的大小是4/8，32位平台（x86）得到的是4，64位平台（x64）得到的是8。

这里补充一个sizeof的知识点

sizeof中的表达式不会参与计算。

3.逻辑操作符

逻辑操作符有 &&（逻辑与） ||（逻辑或），这两个操作符虽然比较简单但是有几个难点还是要详细学习一下。

来看一下这个题目

这里得到的结果为什么是1 2 3 4呢？原因是a++先使用后自增1，a最开始为0，在进行&&操作时，直接为假，后面都不进行，所以得到的结果是1 2 3 4。

逻辑或操作中得到的结果是1 3 3 4，这是为什么呢？逻辑或操作中前面一旦满足情况，后面的就不再进行。

这里也是一样的情况。

总结一下：&&前面为假，后面不进行。||前面为真，后面不进行。

4.逗号操作符

逗号表达式，就是用逗号隔开的多个表达式。逗号表达式，从左向右依次执行。整个表达式的结果是最后一个表达式的结果，来看看这个代码。

这个表达式的结果是3。

5. 条件操作符

exp1 ? exp2 : exp3，三目操作符，这是条件操作符的用法。

6.表达式求值

表达式求值的顺序一部分是由操作符的优先级和结合性决定的。同时，有些表达式的操作数在求值的过程中可能需要转换为其他类型。

6.1.隐式类型转换

C的整型算术运算总是至少以缺省整型类型的精度来进行的。为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

我们来看看这个代码

整形提升是按照变量的数据类型的符号位来提升的

char a = 5;
char b = 126；
char c = a+b；
5的补码是00000000000000000000000000000101
然而char类型只能存8个比特位会产生截断变成00000101，所以a里面放的是这个。
126的补码是00000000000000000000000001111110
char类型只能存放8个比特位，b里面的存放的是011111110
当a和b相加的时候，a和b都是char类型，表达式就要发生整形提升。
a-00000000000000000000000000000101
b-00000000000000000000000001111110
a+b=00000000000000000000000010000011
c也是char类型发生截断变成10000011
打印c的时候，需要原码。
先整形提升
c-11111111111111111111111110000011（补码）
c-10000000000000000000000001111101（原码）
最后得到的结果是-125

这个代码也可以证明整形提升存在。

再来看看这个

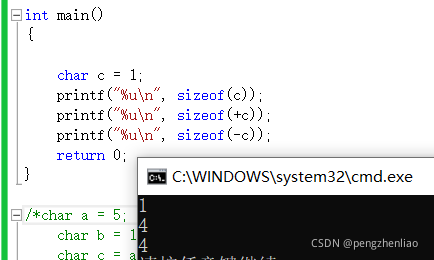
c只要参与表达式运算,就会发生整形提升,表达式 +c ,就会发生提升,所以 sizeof(+c) 是4个字节。表达式 -c 也会发生整形提升,所以 sizeof(-c) 是4个字节,但是 sizeof(c) ,就是1个字节。

6.2 算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

long double， double， float， unsigned long int， long int， unsigned int， int

如果某个操作数的类型在上面这个中排名靠后，那么首先要转换为另外一个操作数的类型后执行运算。

6.3 操作符的属性

复杂表达式的求值有三个影响的因素。

1. 操作符的优先级

2. 操作符的结合性

3. 是否控制求值顺序。（&& || ，？：）

两个相邻的操作符先执行哪个？取决于他们的优先级。如果两者的优先级相同，取决于他们的结合性。

表达式求值，有了优先级和结合性，不一定能得到唯一解。

例如 a*b+c*d+e*f有不同的计算路径。

再有计算c + --c，--的优先级高先算--c再算--c，那么c的值比原来少1，但是有可能先准备好c的值再--c。所以我们在掌握了优先级和结合性后还是要小心。

7.操作符相关题目

#include <stdio.h>
int main()
{
	int a, b, c;
	a = 5;
	c = ++a;
	b = ++c, c++, ++a, a++;
	b += a++ + c;
	printf("a = %d b = %d c = %d\n:", a, b, c);
	return 0;
}

看看这个代码的输出结果是什么？

#include <stdio.h>
int main()
{
	int a, b, c;
	a = 5;
	c = ++a;//c = 6,a = 6,
	b = ++c, c++, ++a, a++;//逗号表达式，这整个构成逗号表达式，所得结果为b=7，c=8，a=8
	b += a++ + c;//这里得到的结果是b=23，c=8，a=9
	printf("a = %d b = %d c = %d\n:", a, b, c);
	return 0;
}

2.统计二进制中1的个数

int count_number_of_1(int n)
{
	int i = 0;
	int count = 0;
	for (i = 0; i < 32; i++)
	{
		if ((n & 1) == 1)
		{
			count++;
		}
		n >>= 1;
	}

	return count;
}
int main()
{
	int n = -1;
	int ret = count_number_of_1(n);

	printf("%d\n", ret);

	return 0;
}

再看看方法2

int count_number_of_1(int n)
{
	
	int count = 0;
	while (n)
	{
		n = n&(n - 1);//这个表达式会把n的二进制序列中最有边的1去掉。
		count++;
	}
	return count;
}
int main()
{
	int n = -1;
	int ret = count_number_of_1(n);

	printf("%d\n", ret);

	return 0;
}

3.求两个数二进制中不同位的个数

#include <stdio.h>
int calc_diff_bit(int m, int n)
{
	int tmp = m^n;
	int count = 0;
	while(tmp)
	{
		tmp = tmp&(tmp-1);
		count++;
	}
	return count;
}
 
int main()
{
 int m,n;
 while(scanf("%d %d", &m, &n) == 2)
 {
     printf("%d\n", calc_diff_bit(m, n));
 }
 return 0;
}

4.打印整数二进制的奇数位和偶数位

void print(int n)
{
	int i = 0;
	for (i = 31; i >= 1; i -= 2)
	{
		printf("%d ",(n >> i) & 1);
	}
	printf("\n");
	for (i = 30; i >=0; i -= 2)
	{
		printf("%d ", (n >> i) & 1);
	}
}

int main()
{

	int a = 0;
	scanf("%d", &a);
	print(a);
	return 0;
}