汉诺（Hanoi）塔问题

汉诺塔的由来

        汉诺塔问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

转化为数学问题

        从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数

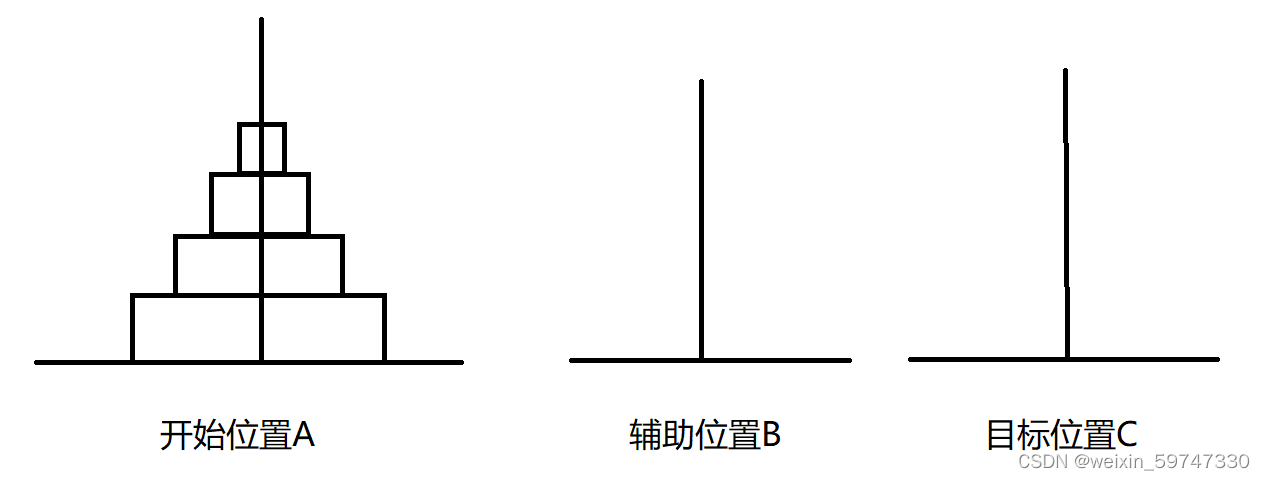
n 为1

第1次  1号盘  A—>C      1 次

n 为 2

第1次  1号盘  A—>B

第2次  2号盘  A—>C

第3次  1号盘  B—>C      3 次

n 为 3

第1次  1号盘  A—>C

第2次  2号盘  A—>B

第3次  1号盘  C—>B

第4次  3号盘  A—>C

第5次  1号盘  B—>A

第6次  2号盘  B—>C

第7次  1号盘  A—>C     7 次

移动次数为：2^n - 1

代码

#include<iostream>
using namespace std;

int sum = 0;

void move(int a, int b, int c)
{
    cout << a << "->" << c << endl;
    sum++; 
}

void hanoi(int n, int a, int b, int c)
{
    if (n == 1)
    {
        move(a, b, c);
    }
    else
    {
        hanoi(n - 1, a, c, b);
        //1.将n-1层圆盘放到辅助位置b
        //2.对于第n-1个圆盘，把b当作目标位置，c当作辅助位置，所以bc互换

        move(a, b, c); 
        // 将最下面的一个圆盘从a移到c上

        hanoi(n - 1, b, a, c); 
        //1.将n-1层圆盘放到目标位置c
        //2.对于n-2层圆盘，a当作辅助位置，b当作开始位置，所以ab互换
    }
}

int main()
{
        int n;
        cout << "请输入移动个数: ";
        cin >> n;
        hanoi(n, 1, 2, 3); 
        cout << "共：" << sum << "步" << endl;
    return 0;
}

结果

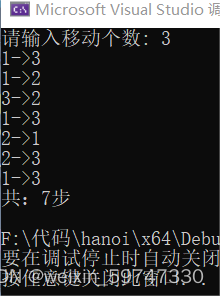
 递归的核心

        递归的核心思想就是把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解

1. 将除最底下的盘子外的所有盘子从柱子A移动到柱子B，利用柱子C作为中转柱子。
2. 将最底下的盘子从柱子A移动到柱子C。
3. 将柱子B上的所有盘子移动到柱子C，利用柱子A作为中转柱子。

        这个过程可以看作是一个递归过程，每次都是将除最底下的盘子外的所有盘子从一个柱子移动到另一个柱子上。当只有一个盘子时，直接将盘子从柱子A移动到柱子C即可。这样，通过递归调用不断解决子问题，最终就可以将所有盘子从柱子A移动到柱子C上。

时间复杂度

        T(N) = 2^N - 1，因此，汉诺塔问题的时间复杂度为O(2^N)